 数値計算
数値計算 ニューラルネット入門(シグモイドで基礎をつなぐ):決定境界→逆伝播→BCEWithLogitsLoss→最適化をNumPyで
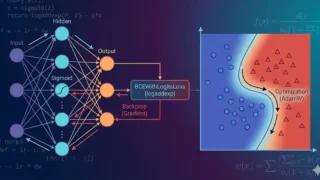
シグモイドで基礎をつなぎ、決定境界の可視化→誤差逆伝播→BCEWithLogitsLoss(logaddexp)→最適化までをNumPyの最小コードで解説します。logが「自信満々の誤り」を強く罰する理由、勾配チェックで逆伝播を検証する方法、AdamWとL2正則化の違い、pos_weightによる不均衡データ対応、NumPyの式がPyTorch APIに一致する最短ブリッジもまとめます。