「引用は出典リンク必須・必要最小限」「FAQ全文転載・図表転載は禁止」「社内資料/研修利用は要連絡」
その他のエッセイはこちら
この記事は、
「完全に理解した/何もわからない/チョットデキル」 というミームを
ダニング=クルーガー効果やハイプサイクルになぞらえて、
ロジスティック関数+山と谷 の「おもちゃモデル」で眺めてみる話です。
最初に重要な断りを置いておきます。
- ここで出てくる数式は、厳密な心理モデルではありません。
- 「ネットミームを数式にして遊んでみる」ための おもちゃモデル です。
- パラメータにも、実証研究に基づいた経験的な意味づけはしていません。
ダニング=クルーガー効果(以下、D-K 効果)そのものも、
近年は「通俗的な図の描き方は統計的アーティファクトでは?」という批判・再検討が増えています。
その上で、
- ざっくりした 直感レベルの D-K 効果/ハイプサイクルの形
- それを 連続関数で描いたらどう見えるか
- 生成AI時代には この形がどう歪むか
といったあたりを、数理好き向けに軽くいじってみる、というスタンスです。
TL;DR
- ネットの「完全に理解した/何もわからない/チョットデキル」ミームを、D-K 効果とハイプサイクルの“山と谷”として眺め直す話です。
- 「本当の理解度」 B(t) と「自信」 C(t) を別々の連続関数として置き、ロジスティック関数+ガウス型の山と谷からなるおもちゃモデルで可視化します。
- 3つのレバー(理解の伸びスピード k、最初のハイプの高さ、幻滅の谷の深さ)で、「学び方のキャラ」を遊び半分に分類します。
- 生成AIを使うと、B(t) は上がる一方で C(t) が全体的に上にシフトしやすいかもしれない──という最近の研究にも軽く触れます。
この文章でやりたいこと
ざっくり言うと、この記事は次のことをやります。
- ネットでよく見る
> 完全に理解した → 何もわからない → チョットデキル
という 3コマの感情変化 を、
D-K 効果の “山と谷” とハイプサイクルの形に重ねてみる。 - 「もしこれを連続関数で表すとしたら?」という
おもちゃモデル $B(t), C(t)$ を 1 本用意 してみる。 - そのモデルにはいくつかの レバー(パラメータ) があるので、
それを「学び方の違い」としてゆるく解釈してみる。 - 最後に、生成AI時代 には
このカーブそのものがどう変わりつつあるかを、
最近の研究例をネタに少しだけ眺める。
ダニング=クルーガー効果とは? ─ 直感として「たぶん正しい」
D-K 効果のざっくりしたイメージ
D-K 効果は、ざっくり言うと:
ある分野で 能力が低い人ほど自分を過大評価しやすく、
能力が高い人はむしろ 自分をやや控えめに評価しがち である
という自己評価バイアスのことだと説明されます。
古典的な実験では、
- 参加者にテストを解いてもらう
- その後、「自分は他の人と比べてどれくらいできたと思うか?」を自己評価してもらう
という手順を踏み、
実際の得点と自己評価を比較 しました。
結果としてよく紹介されるのは:
- 下位グループは、自分を 平均よりかなり上 にいると評価しがち
- 上位グループは、自分を ほぼ正確か、やや控えめ に評価する傾向がある
というパターンです。
この話がミーム化していく中で、横軸を「本当のスキル」、縦軸を「自信」にしたグラフ上に、
- 最初の「完全に理解した」ピーク
- そこから落ち込む 「何もわからない」谷
- 最終的に落ち着く 「現実的な自信」
という 山と谷がある曲線 として描かれることが増えました。
ただし「通俗 D-K グラフ」にはツッコミも多い
ここで一度、ブレーキを踏んでおきます。
近年の研究では、
- D-K 効果のデータのかなりの部分は、
回帰効果 +「自分は平均より上でありたい」という一般的バイアス で
説明できてしまうのではないか?
という指摘もあります。
つまり、ネットでよく見るような
「無能な人ほどバカみたいに自信満々」
「有能な人はみんな謙虚」
といった劇画調の解釈は、
だいぶ盛ったバージョン だと考えた方が安全です。
この記事では、そのことを踏まえたうえで、
- あくまで 通俗的に描かれる D-K グラフの“形”だけを借りて
- 「完全に理解した」ミームを数式で眺めてみる
という立場を取ります。
もう一度強調すると、
ここで出てくる数式は、D-K 効果そのものを厳密に説明するモデルではありません。
「ミームの形を連続関数にして遊ぶ」ための おもちゃモデル です。
「完全に理解した」ミームを時間軸に乗せてみる
三つの離散状態
まずは、よくある 3 コマを 時間順の離散状態 として眺めます。
- 完全に理解した
- チュートリアルを 1 本読んだ
- サンプルコードをコピペして動かした
- 解説ブログを数本読んだ
→ 「あ、思ってたより簡単じゃん。完全に理解した」
- 何もわからない
- 自分でゼロから組んでみたら動かない
- エッジケースや例外処理が多くて沼にハマる
- 実務フローに乗せようとしたら前提がぜんぜん違う
→ 「あれ、自分が分かっていたのって、
すごく薄い上澄みだったのでは…?」
- チョットデキル
- 何度か実務で使ってみる
- 「ここまでは説明できる」「ここから先はまだ怪しい」という
範囲付きの自信 に落ち着く
→ 「完全に理解したとは言えないけど、
実務上はこれくらい分かっていれば十分かな」
この 3 点を、時間 $t$ の関数としての自信 $C(t)$ の
- ピーク(完全に理解した)
- 谷(何もわからない)
- 後半のゆるい上昇(チョットデキル)
として見ると、
それっぽい “ハイプサイクル型” のカーブ を描けそう、という気がしてきます。
ハイプサイクルとは?
ここで一度、ハイプサイクル側のおさらいもしておきます。
ガートナーの Hype Cycle(ハイプサイクル) は、
- Technology Trigger(技術トリガー)
- Peak of Inflated Expectations(過度な期待のピーク)
- Trough of Disillusionment(幻滅期)
- Slope of Enlightenment(啓蒙の坂)
- Plateau of Productivity(生産性の高原)
という 5 フェーズで、新技術への期待の上下を図示したフレームワークです。
これも D-K 効果と同じく、
- すべての技術が必ずこの形を通るわけではない
- 実データとぴったり合うとは限らない
といったツッコミはもちろんあるのですが、
「この技術、今どのフェーズっぽい?」と雑に話すための共通言語 として便利なので、よく見かけます。
この記事では、この ハイプサイクルの形 を個人の学びに持ち込んで、
「自分ごとのハイプサイクル」
=「完全に理解した → 何もわからない → チョットデキル」
として眺めてみる、という遊び方をします。
連続関数で「完全に理解したカーブ」を描いてみる(おもちゃモデル)
ここから少しだけ数式の話に入ります。
もう一度:これはおもちゃモデルです
念押しになりますが、
- 実データにフィットさせたモデルではありません。
- パラメータを動かしても、実験的・臨床的な意味はありません。
- 「D-K の真の構造はこれだ」と主張したいわけでもありません。
「完全に理解した 3 コマ」を
ハイプサイクル型の連続曲線として描くとしたら
こんな関数でも遊べるよね、という
数理イラスト だと思ってください。
ベースライン:ロジスティックで「本当の理解」を表す
まず、時間とともにじわじわ増えていく
「本当の理解度」 を、$B(t)$ という関数で表します。
ここでは扱いやすさのために、理解度の上限を 1 に正規化しておきます。
$$
B(t) = \frac{1}{1 + e^{-k (t – t_0)}}
$$
- $t$:学び始めてからの時間(0〜1 に正規化しておく)
- $k$:どれくらいのスピードで理解が伸びるか
- $t_0$:伸びが一番速くなるあたりの時刻
この定義だと、常に $0 \leq B(t) \leq 1$ になります。
単純に、
- 最初はゆっくり
- 中盤で一気に伸び
- 後半は頭打ちになって高原に落ち着く
という「よくある学習曲線の形」を、ロジスティックでざっくり描いているだけです。
ハイプの山と幻滅の谷:ガウス型の山と谷を足し引きする
次に、自信(自己評価) を $C(t)$ として、
以下の 2 つを別々の項として用意します。
- 早い段階で一瞬だけ大きく盛り上がる ハイプの山
- そのあとやってくる 幻滅の谷
ハイプの山をガウス関数で表すと:
$$
H(t) = A_\mathrm{hype}\,\exp\left(
-\frac{(t – t_\mathrm{hype})^2}{2\sigma_\mathrm{hype}^2}
\right)
$$
幻滅の谷も同様に(符号はあとでまとめて扱うので、とりあえずプラスで定義):
$$
V(t) = A_\mathrm{valley}\,\exp\left(
-\frac{(t – t_\mathrm{valley})^2}{2\sigma_\mathrm{valley}^2}
\right)
$$
ここで、
- $A_\mathrm{hype}$:「完全に理解した」ピークの高さ
- $A_\mathrm{valley}$:「何もわからない」谷の深さ
- $t_\mathrm{hype}$, $t_\mathrm{valley}$:山と谷が現れるタイミング
- $\sigma_\mathrm{hype}$, $\sigma_\mathrm{valley}$:それぞれの幅
です。
合成して「自信カーブ」 $C(t)$ を作る
自信のカーブ $C(t)$ を、単純に
$$
C(t) = B(t) + H(t) – V(t)
$$
と置くと、
- 最初に $H(t)$ が効いて 「完全に理解した」っぽいピーク が立ち、
- その後 $V(t)$ によって 「何もわからない」谷 ができ、
- 全体としては $B(t)$ に引き寄せられて、
後半は 「チョットデキル」程度の落ち着いた自信 に収束する
という、それっぽい形 の曲線が描けます。
パラメータはたくさん出てきましたが、
人間側の解釈としては次の 3 つのレバー だけ意識しておけば十分です。
- $k$:本当の理解 $B(t)$ の伸びスピード
- $A_\mathrm{hype}$:最初のハイプの大きさ(どれだけ「完全に理解した」と思い込むか)
- $A_\mathrm{valley}$:幻滅の谷の深さ(どれだけ「何もわからない」に落ち込むか)
残りのパラメータ($t_\mathrm{hype}$, $t_\mathrm{valley}$ や各 $\sigma$ )は、
図がそれっぽく見えるように 適当に固定 してしまって構いません。
Python で「本当の理解」と「自信」のズレを描いてみる
ここからは、上のアイデアをそのまま Python にしてみた例です。
ブログの図用のおもちゃコード だと思ってください。
B(t) と C(t) を同時にプロットする
import numpy as np
import matplotlib.pyplot as plt
def base_skill(t, k=4.0, t0=0.7):
"""本当の理解度 B(t):ロジスティック(上限1に正規化)"""
return 1 / (1 + np.exp(-k * (t - t0)))
def hype_bump(t, A_h=0.9, t_h=0.25, sigma_h=0.10):
"""最初の「完全に理解した」ハイプの山"""
return A_h * np.exp(- (t - t_h)**2 / (2 * sigma_h**2))
def valley_bump(t, A_v=0.7, t_v=0.5, sigma_v=0.08):
"""「何もわからない」の谷(あとで引くのでプラスで定義)"""
return A_v * np.exp(- (t - t_v)**2 / (2 * sigma_v**2))
def confidence_curve(t,
k=4.0,
A_h=0.9,
A_v=0.7):
"""自信のカーブ C(t)"""
B = base_skill(t, k=k)
H = hype_bump(t, A_h=A_h)
V = valley_bump(t, A_v=A_v)
return B + H - V
t = np.linspace(0, 1, 400)
B = base_skill(t)
C = confidence_curve(t)
plt.figure(figsize=(8, 4))
plt.plot(t, B, label="base_skill B(t)")
plt.plot(t, C, label="confidence C(t)")
plt.xlabel("learning time (t)")
plt.ylabel("level")
plt.title("Toy model of 'true understanding' vs. 'confidence'")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
この図では、
- ロジスティックな 本当の理解度 $B(t)$
- そこに「山と谷」が乗ってできた 自信カーブ $C(t)$
が同時に見えるので、
「本当の理解 B(t) と、自信 C(t) のズレ」 が直感的に把握しやすくなります。
レバーをいじって「低ハイプ型」も描いてみる
同じ図の上に、「ハイプ弱め・谷浅め」の別パターンを 1 本だけ重ねると、
レバー($A_\mathrm{hype}$, $A_\mathrm{valley}$)をいじって遊べる感 が出ます。
# デフォルトの C(t)
C_default = confidence_curve(t)
# 「ハイプ小さめ・谷浅め」タイプの C(t)
C_low_hype = confidence_curve(t, A_h=0.2, A_v=0.5)
plt.figure(figsize=(8, 4))
plt.plot(t, B, label="base_skill B(t)")
plt.plot(t, C_default, label="confidence (default)")
plt.plot(t, C_low_hype, label="confidence (low hype)")
plt.xlabel("learning time (t)")
plt.ylabel("level")
plt.title("Effect of hype/valley parameters on confidence C(t)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()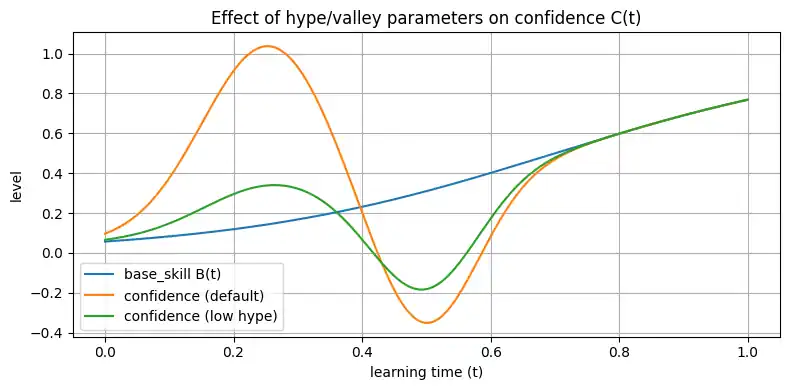
こんな感じで、パラメータを 1 行変えてプロットし直すだけで、
「学び方のキャラ」の違いが図として感覚的に見えてきます。
レバーをいじって「学び方のキャラ」を見てみる
さきほどの 3 つのレバーをおさらいすると:
- $k$:本当の理解 $B(t)$ の伸びスピード
- $A_\mathrm{hype}$:最初のハイプの大きさ
- $A_\mathrm{valley}$:幻滅の谷の深さ
これを「学び方のキャラクター」として、
深刻になりすぎない程度に眺めてみます。
上澄みだけさらっとタイプ
- チュートリアルを一周して「完全に理解した」と言いがち
- その後、実務であまり深追いしない
というタイプをイメージすると、
- $A_\mathrm{hype}$:大きい(最初の山が高い)
- $A_\mathrm{valley}$:浅い(谷に落ちる前に別のネタに移る)
- $k$:それほど大きくない(本当の理解はあまり伸びない)
というパラメータになるでしょう。
params_skim = dict(k=2.0, A_h=1.0, A_v=0.25)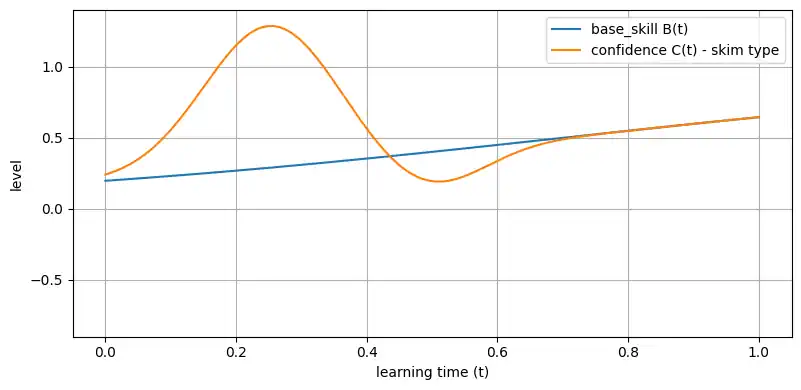
そこそこ周りを見る現実派
- 早い段階で「いや、そんな簡単じゃないよね」と気づきやすい
- 自分の理解と周囲のレベルを見比べるクセがある
という人は、
- $A_\mathrm{hype}$:中くらい(最初からそこまで舞い上がらない)
- $A_\mathrm{valley}$:中くらい(落ち込むけれど、ほどほどで戻る)
- $k$:そこそこ大きい(安定した学び)
くらいのカーブになります。
params_balanced = dict(k=3.5, A_h=0.6, A_v=0.6)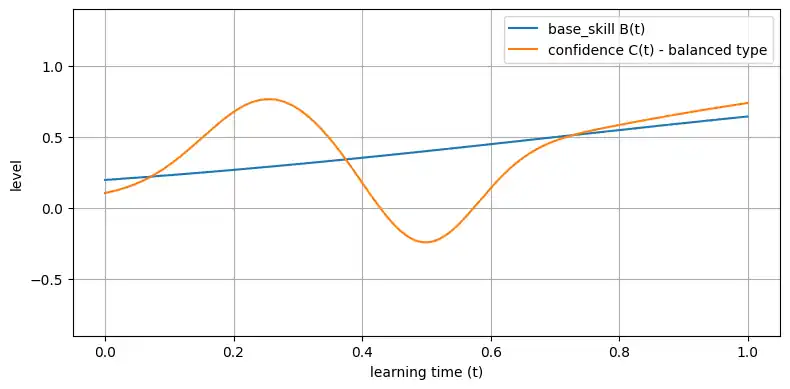
理屈ガチ勢・沼りがちタイプ
- 「原著論文や仕様書を読まないと『分かった』と言いたくない」
- 一度「何もわからない」の深い沼に沈みがち
という人は、
- $A_\mathrm{hype}$:小さめ(そもそも「完全に理解した」とは言わない)
- $A_\mathrm{valley}$:大きい(谷が深い)
- $k$:大きい(いったん抜けたら理解度は高い)
というカーブになるはずです。
params_deep = dict(k=5.0, A_h=0.25, A_v=1.1)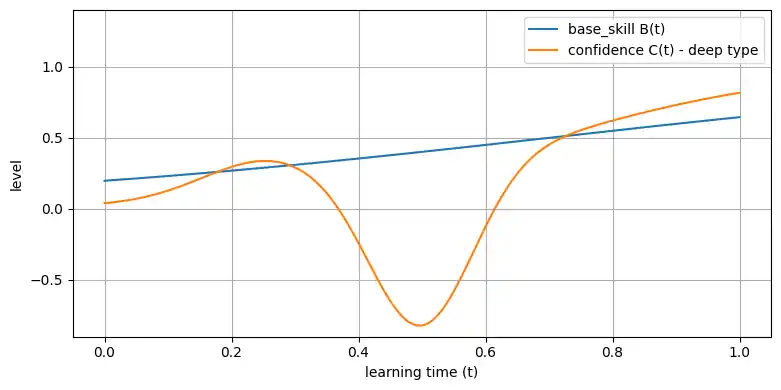
もちろん、どれが良い/悪いという話ではありません。
「自分はいま、どのレバーを強めに回している状態なんだろう?」
と眺めてみるための 自己観察ツール として使う、くらいがちょうどよいです。
明日から使える(かもしれない)「完全に理解したフレームワーク」
せっかくなので、このおもちゃモデルを
実務や勉強でギリギリ使えるレベル までざっくり落としておきます。
フェーズを「自己ラベル」として使う
新しい技術や分野を学ぶときに、
自分の状態をあえて次の 3 つのどれかにラベリングしてみます。
- 完全に理解したフェーズ
- チュートリアルを一周して、手も動かした
- 「分かった気になっているかもしれない」と自覚する段階
- 何もわからないフェーズ
- 例外や現実の制約を見て、「思ってたのと違う」段階
- ここで 投げ出すか・踏ん張るか が分かれ目
- チョットデキルフェーズ
- 「ここまでは説明できる」「ここから先はまだ怪しい」と
自分で範囲を切って話せる段階
- 「ここまでは説明できる」「ここから先はまだ怪しい」と
大事なのは、今の自分がどこにいるかを意識しておくこと です。
- 「完全に理解したフェーズ」だと分かっていれば、
あえて反対側の情報を取りに行ったり、 - 「何もわからないフェーズ」にいることを自覚していれば、
実は $B(t)$ は伸びているのに $C(t)$ だけが落ちている、と気づけます。
他人に貼るのではなく、自分のメタ認知に使う
このフレームワークは、
他人を「お前は完全に理解したフェーズだな」と切るための武器 にすると、
ほぼ確実に人間関係が壊れます。
そうではなく、
- 「自分はいま $A_\mathrm{hype}$ を上げすぎていないか?」
- 「そろそろ $A_\mathrm{valley}$ が大きくなってきたから、
一度アウトプットして整理した方がいいかも」
といった セルフチェック に使うのが穏当です。
生成AI時代には C(t) の形そのものが変わるかもしれない
最後に、生成AIとの関係を少しだけ。
ChatGPT と自己評価バイアスの最近の研究
最近の研究では、ChatGPT のような生成AIを使ったタスクで、
- 実際の得点は上がる のに、
- 参加者が 自分の成績をさらに大きく過大評価しやすくなる
という結果が報告されています。
ざっくり言うと、
- AI 支援なしで問題を解いたときよりも、
- AI を使ったときの方が、
「自分はかなりできたはずだ」という自信が 強くなりすぎる 傾向がある。
さらにおもしろいのは、
- 「AI の性能やリスクについて理解している」と自己申告した人ほど、
- 自分の成績の見積もりと実際の得点の差が 大きくなっていた
という点です。
つまり、生成AIをがっつり使い始めると、
「本当の能力(B(t))は上がるけれど、
自信カーブ C(t) が全体的に 上にシフト してしまう
可能性がある、ということになります。
おもちゃモデル的な解釈
この記事の $C(t)$ で言えば、
- 自分の能力だけで学んでいるときは、
「最初の山 $H(t)$ → 谷 $V(t)$ → ベースライン $B(t)$」という 3 段構成。 - 生成AIを併用した学びでは、
- ベースライン $B(t)$ 自体が押し上げられつつ、
- どのフェーズにいても +定数のオフセット が乗っているような $C(t)$ になる。
とイメージできます。
このとき、悪いパターンとしては、
- 早い段階で AI に答えを丸投げし、
- その結果だけを見て 「自分はだいぶ分かっている」と錯覚する
という意味で、
「谷を経験しないまま plateau に乗ってしまう」 ような学び方になることです。
一方で、AI の使い方を工夫すれば、
- 自分の解答と AI の解答を比較する
- AI に「自分の説明の穴」を突いてもらう
といった形で、むしろ メタ認知(B と C のズレの自覚)を助ける使い方 もできます。
生成AI時代の学びでは、
「C(t) がどの方向に歪んでいるか」を意識しながら AI を使う
という設計が、これからますます重要になりそうです。
まとめ:本当の理解 B(t) と自信 C(t) のズレを眺める
最後に、本記事のポイントだけまとめておきます。
- 「完全に理解した/何もわからない/チョットデキル」というネットミームを、
- ダニング=クルーガー効果とハイプサイクルになぞらえて、
- 「本当の理解度」 $B(t)$ と「自信」 $C(t)$ の 2 本の曲線として眺めてみた。
- $B(t)$ はロジスティック関数で、上限を 1 に正規化した なめらかな学習曲線。
- $C(t)$ は $B(t)$ に、
- 早期のハイプの山 $H(t)$
- 中盤の幻滅の谷 $V(t)$
を足し引きした おもちゃモデル として定義した。
- このとき、
- 本当の理解の伸びスピード $k$
- 最初のハイプの大きさ $A_\mathrm{hype}$
- 幻滅の谷の深さ $A_\mathrm{valley}$
の 3 つを、学び方の レバー(キャラクター) として解釈できる。
- さらに、生成AIの導入によって、
- $B(t)$ 自体は押し上げられる一方で、
- $C(t)$ が全体的に上にシフトし、
「谷を飛ばして plateau だけ味わってしまう」危険も出てくる。
もう一度念押しすると、
ここで使ったモデルは 心理学的に厳密なものではありません。
「みんながなんとなく共有しているミーム」を
一度連続関数にして眺めると、
「レバー」や「形の変化」として語り直せる部分も見えてくる
そのくらいの 数理遊び として、
どこかで役に立てばうれしいです。
FAQ
Q1. ダニング=クルーガー効果とは何ですか?
A1. ある分野で能力が低い人ほど、自分の能力を実際より高く見積もりやすい、という自己評価のバイアスを指します。元の研究では、テスト成績と「自分はどれくらいできたか」という自己評価を比べたとき、下位グループほど過大評価が大きい傾向が報告されました。ただし、近年の研究では統計的な回帰効果や「自分は平均より上だと思いたい」バイアスでもかなり説明できるのではないか、という議論もあります。
Q2. この記事の数式は、どれくらい心理学的に厳密ですか?
A2. 本文中で繰り返し書いたとおり、あくまでおもちゃモデル です。実際のデータに当てはめたわけでもなく、パラメータに臨床的な意味を持たせてもいません。ネットで流通している「通俗的な D-K グラフ」や「完全に理解したミーム」の形を、ロジスティック関数とガウス関数でスケッチしたもの、と捉えてください。
Q3. ハイプサイクルとは何ですか?
A3. ガートナーが提案したフレームワークで、新技術が登場してから成熟・定着するまでの過程を、時間と期待値のグラフとして 5 つのフェーズで表現したものです。テクノロジー・トリガー、過度な期待のピーク、幻滅期、啓蒙の坂、生産性の高原という段階を想定し、技術トレンドを議論するときの共通言語として広く使われています。
Q4. 生成AIはダニング=クルーガー効果をどう変えますか?
A4. 最近の研究では、ChatGPT などの生成AIを使うとタスクの正答率は向上する一方で、参加者が自分の成績を大きく過大評価する傾向が強まることが報告されています。従来の D-K 効果のような「下位ほど過大評価が大きい」パターンは弱まり、能力レベルにかかわらず 全体的な過信(オーバーコンフィデンス) に近い形になる、という指摘もあります。
Q5. 「完全に理解したフレームワーク」はどう使えばよいですか?
A5. 他人を評価するラベルとしてではなく、自分の学習状態を確認するためのメタ認知ツール として使うのがおすすめです。新しい分野を学ぶときに、「完全に理解した」「何もわからない」「チョットデキル」のどこにいるかを意識的に言語化することで、自信の過不足や生成AIへの依存度を調整しやすくなります。
「引用は出典リンク必須・必要最小限」「FAQ全文転載・図表転載は禁止」「社内資料/研修利用は要連絡」
参考文献(公的・学術寄り・URL付き)
※以下は本文で触れた話題の背景情報としての参考であり、
本文中の数式モデルがこれらに基づいているわけではありません。
- Kruger, J., & Dunning, D. (1999).
Unskilled and Unaware of It: How Difficulties in Recognizing One’s Own Incompetence Lead to Inflated Self-Assessments.
Journal of Personality and Social Psychology.
https://doi.org/10.1037/0022-3514.77.6.1121 - Dunning–Kruger effect | Wikipedia(英語版、D-K 効果の定義と議論の整理)
https://en.wikipedia.org/wiki/Dunning%E2%80%93Kruger_effect - Gignac, G. E., & Zajenkowski, M. (2020).
The Dunning–Kruger effect is (mostly) a statistical artefact: Valid approaches to testing the hypothesis with individual differences data.
Intelligence, 80, 101449.
https://www.sciencedirect.com/science/article/pii/S0160289620300271 - A Statistical Explanation of the Dunning–Kruger Effect.
Frontiers in Psychology.
https://www.frontiersin.org/articles/10.3389/fpsyg.2022.840180/full - Dunning–Kruger effect | Britannica(ブリタニカによる概説記事)
https://www.britannica.com/science/Dunning-Kruger-effect - Gartner hype cycle | Wikipedia(ハイプサイクルの概説)
https://en.wikipedia.org/wiki/Gartner_hype_cycle - 「ガートナーのハイプ・サイクルとは何ですか?」 | ガートナージャパン公式(日本語解説)
https://www.gartner.co.jp/ja/articles/gartner-hype-cycle - Fernandes, D., et al. (2025).
AI makes you smarter but none the wiser: The disconnect between performance and metacognition.
Computers in Human Behavior(早期公開版)
https://www.sciencedirect.com/science/article/pii/S0747563225002262
プレプリント PDF: https://arxiv.org/pdf/2409.16708 - Aalto University / Live Science 記事(AI 利用と自己評価バイアス)
https://www.livescience.com/technology/artificial-intelligence/the-more-that-people-use-ai-the-more-likely-they-are-to-overestimate-their-own-abilities
その他のエッセイはこちら
完全に理解した
チョットデキル
ダニング=クルーガー
認知バイアス



コメント