その他のエッセイはこちら
「虚数って、結局なんなんだろう？」
「フーリエ変換に必ず i（虚数）が出てくるけど、あれ何をしているの？」
理系の授業や技術書を読んでいて、一度はそう思ったことがある人も多いはずです。
教科書ではいきなり
- $\sqrt{-1} = i$
- $a + bi$ を 複素数 と呼ぶ
- フーリエ変換の式にいきなり $e^{-i\omega t}$ が出てくる
といった形で登場するので、「ルールとしては分かるけど、なぜそうするのかが腑に落ちない」という状態になりがちです。
ここでは、あえて最初から原理主義で攻めるのではなく、
- 「反復」や「周期」といった直感的なところからスタートして
- 虚数・複素数を「回転」を表すための道具として捉え直し
- 最後に フーリエ変換の直感 につながるところまで
を目標にします。
厳密な証明や難しい記号は最小限にして、
「ああ、虚数って“回転と周期”を扱うための座標拡張なんだな」
くらいの手触りを持ってもらえることをゴールにしています。
※ 微分やフーリエ変換の式も少しだけ出てきますが、「変化のしかたを調べる道具」くらいのイメージで読んでもらえれば十分です。細かいところは“雰囲気で”流して OK です。
実はこの話の元ネタは、社会人2〜3年目のときに高校で話をしたときの内容です。物理の先生をしている知人に「社会人の観点で物理や数学の話をしてほしい」と言われて、高校生相手に虚数やフーリエ変換の話をしました。そのときも「虚数って結局なに？」「なんでフーリエ変換に i が出てくるの？」という質問が一番多く、今回まとめている内容も、あのときのやりとりの延長線上にあります。
虚数とは何か？「反復」と「符号反転」から考える
まず、「虚数とは何か」を考える前に、
もっと素朴なところから順番にたどってみます。
自然数：ただひたすら右に進む世界
一番最初に出てくるのは 自然数 です。
$$
1, 2, 3, 4, \dots
$$
これは「1本の線の右側」にだけ点が並んでいるイメージです。
増える方向にしか進めません。
- 1個
- 2個
- 3個
と、「数える」「足していく」には十分ですが、
- 逆向きに戻る
- 行ったり来たりする
といった動きは表しづらい世界です。
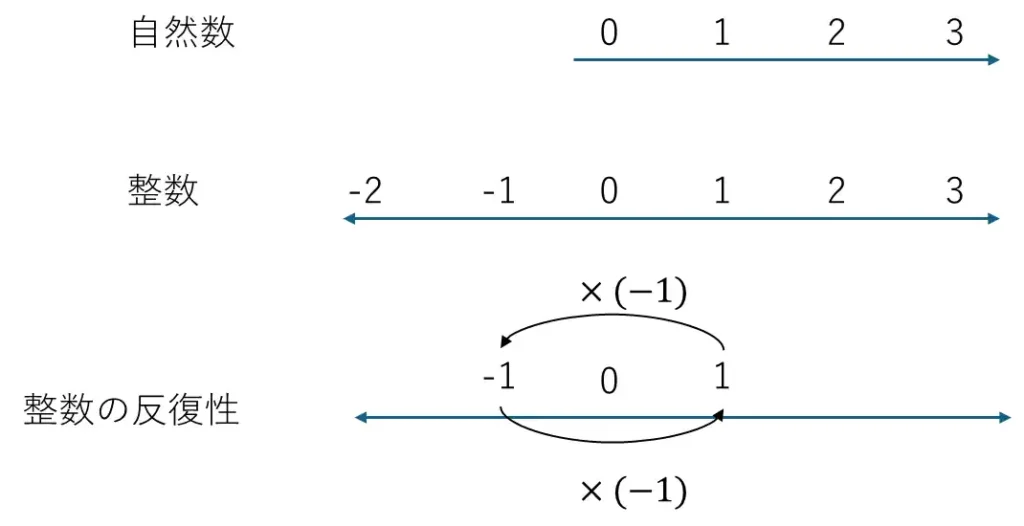
整数：行ったり来たりできるようになる
そこで登場するのが 整数 です。
$$
\dots, -3, -2, -1, 0, 1, 2, 3, \dots
$$
0 を真ん中にして、左にマイナス、右にプラスが並ぶ「数直線」がイメージしやすいと思います。
このとき、たとえば 1 に対して「-1 を掛け続ける」ことを考えると：
- 1 × (-1) = -1
- -1 × (-1) = 1
- さらに × (-1) = -1
…
と、1 と -1 のあいだをひたすら往復します。
これはごく単純な「反復」や「振動」のモデルになっています。
ただし、この世界はまだ 1次元の中での符号反転だけです。
- 右か左か
- プラスかマイナスか
といった、“行ったり来たり”だけを表現している状態です。
ここから先、
もっとなめらかな「周期」や「回転」を表したくなると、
1本の軸だけでは足りなくなってきます。
そこで、いよいよ 虚数・複素数の出番になります。
なぜ虚数が必要なのか：周期や回転を表すための「もう1本の軸」
整数までの世界では、
- 「増える・減る」
- 「プラス・マイナス」
- 「行ったり来たり」
といった動きは表現できます。
しかし、現実の物理現象や信号には、もっとなめらかな「周期」や「回転」がよく登場します。
- 円運動
- 振り子の揺れ
- 電気信号の波形
- 音や振動の波
などは、単なる「プラスかマイナスか」ではなく、
- どれくらいの速さで
- どれくらいの大きさで
- どれくらい位相（タイミング）がずれているか
といった情報を持っています。
1本の数直線（実数軸）だけでは、この「位相」や「回転」の情報をきれいに扱うことができません。
そこで登場するのが、虚数軸という、実数と直交するもう1本の軸です。
- 横軸：実数（いままでの数直線）
- 縦軸：虚数（新しく導入する軸）
この2本の軸でつくられる平面を 複素平面 と呼びます。
ここでは、複素平面を
「周期や回転を扱うために、数直線を2次元に拡張したもの」
くらいに思っておいて構いません。
i を掛けると90度回転する：複素数の「回転」の直感
虚数単位 $i$ は、ふつう
$$
i^2 = -1
$$
という式から説明されますが、ここでは少し視点を変えます。
複素平面の上で、
- 右方向（実数 1 の位置）からスタートして
- $i$ を掛ける操作を、「ベクトルを 90度左回りに回転させること」
だと考えてみます。
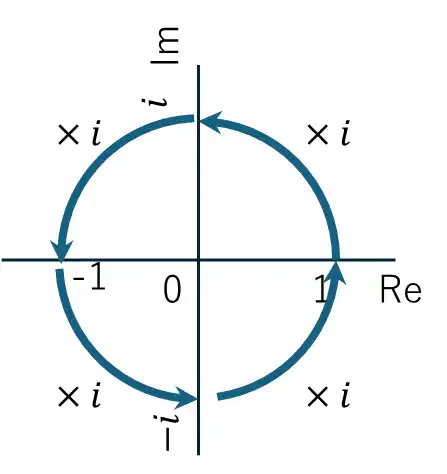
実際に 1 に i を掛けていくと：
- $1 \times i = i$
→ 右から上へ（90度回転） - $i \times i = i^2 = -1$
→ 上から左へ（180度回転） - $-1 \times i = -i$
→ 左から下へ（270度回転） - $-i \times i = i^3 \times i = i^4 = 1$
→ 下から右へ（360度回転して元に戻る）
このふるまいだけを見ると、
「i を掛ける = 複素平面で 90度回す演算」
とみなすのが自然に感じられます。
この見方を採用すると、
- 「i² = -1」は「90度回転を2回やると、数直線の反対側に行く」
- 「i³ = -i」「i⁴ = 1」も「回転を3回・4回」という意味
として理解できます。
ここでは、
虚数 i は「√-1 という謎の数」ではなく、
「回転を表すために導入された記号」
という直感を持っておきます。
実際に、一般の複素数 $x+iy$ に $i$ を掛けると
$i(x + iy) = ix – y = -y + ix$となり、座標としては$(x, y) \rightarrow (-y, x)$という「90度回転」になっていることがわかります。
ここでは「$i$ を掛ける操作＝90 度回転」とみなす直感を優先しています。
厳密な定義としては、複素数全体を「実数を 2 次元に並べたもの」として定義し、その上で掛け算を決めた結果として「$i$ を掛けると回転になる」と分かる、という順番になります。
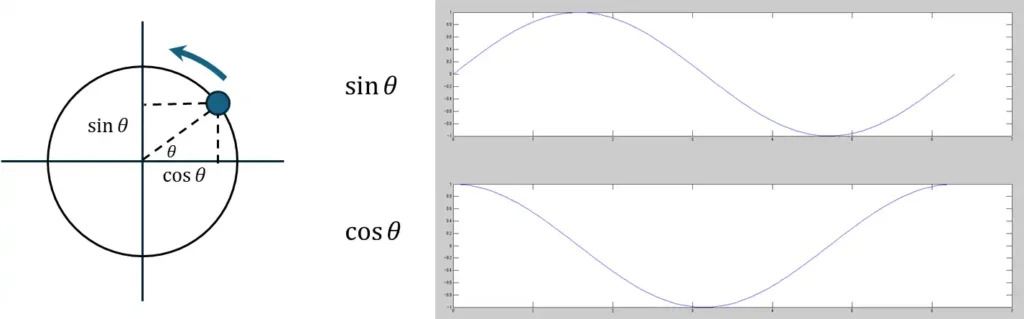
sin, cos と虚数の関係：微分すると位相がずれるだけ
次に、「周期」や「回転」といえばおなじみの 三角関数 です。
角速度 $\omega$、時間 $t$ を用いて
$$
\sin(\omega t), \quad \cos(\omega t)
$$
を考えます。
これらを時間で微分すると、
$$
\frac{d}{dt}\sin(\omega t) = \omega \cos(\omega t)
$$
$$
\frac{d}{dt}\cos(\omega t) = -\omega \sin(\omega t)
$$
という関係が成り立ちます。
ここからわかることは：
- 微分しても「sin と cos という形」は変わらない
- ただし
- 振幅が $\omega$ 倍され
- 位相が ±90度（$\pi/2$）ずれる
ということです。
つまり、sin, cos は
「微分すると、位相がシフトするだけで済む」
微分と相性のいい周期関数
になっています。
物理や工学で振動・波・信号が出てくるときに
$\sin$ や $\cos$ が頻出するのは、単に「きれいな式だから」だけではなく、
- 微分方程式との相性が良く
- 周期・振動を表すのに都合が良い
という背景があります。
オイラーの公式で三角関数を複素平面に閉じ込める
ここで、虚数と三角関数が一気につながります。
カギになるのが、有名な オイラーの公式 です。
$$
e^{i\theta} = \cos\theta + i\sin\theta
$$
この式から、
- 実部：$\cos\theta$
- 虚部：$\sin\theta$
として、cos と sin をひとつの複素数にまとめて表現できることがわかります。
時間依存の形で書くと、
$$
e^{i\omega t} = \cos(\omega t) + i\sin(\omega t)
$$
となります。
さらに重要なのは、これを時間微分したときのふるまいです。
微分にあまり馴染みがない人は、「時間がちょっと進んだときの変化のしかたを調べる操作」くらいのイメージで読んでもらえれば大丈夫です。
$$
\frac{d}{dt}e^{i\omega t} = i\omega e^{i\omega t}
$$
つまり、
「時間で微分する」という操作が、
複素平面の上では 「$i\omega$ を掛ける」 という単純な形に変わっている
ということです。
ここには、
- $i$：90度回転（位相シフト）の要素
- $\omega$：回転の速さ（周波数）の要素
が含まれています。
これまで見てきた
- sin, cos を微分すると位相がずれる
- i を掛けると回転する
という二つの性質が、$e^{i\omega t}$ の微分という一行の式に融合している、とも言えます。
ここまで来ると、
「三角関数（sin, cos）を複素平面に閉じ込めることで、
微分が“掛け算”になって扱いやすくなる」
というイメージが見えてきます。
フーリエ変換の直感：どんな信号も「回転の足し合わせ」
いよいよ、フーリエ変換の直感的なイメージに触れておきます。
ざっくり言えば、フーリエ変換は
「どんな波形（信号）でも、いろいろな速さの
回転（＝周期波）の足し合わせとして分解してしまおう」
- 時間領域では、信号はゴチャゴチャした形をしている
- でもそれを「周波数ごとの成分」に分けて眺めると
- どの周波数が
- どれくらいの強さ（振幅）で
- どれくらいタイミング（位相）がずれているか
という情報に分解できます。
雰囲気だけ書くと、フーリエ変換は
$$
F(\omega)=\int_{-\infty}^\infty f(t)\,e^{-i\omega t}\,dt
$$
のような形をしていて、「信号$f(t)$と、周波数$\omega$で回る波$e^{-i\omega t}$がどれくらい“重なっているか”を調べる式（内積のようなもの）だと思っておくとイメージしやすいです。ここでは雰囲気だけ掴んでもらえれば十分です。
教科書によって、e の肩の符号や 2π の付き方など細部は少しずつ違いますが、どれも「回転する波との重なり具合を調べる」という本質は同じです。
ここではイメージをつかみやすくするために、係数の違いは省略しています。
このときの「基本パーツ」が、さきほど出てきた
$$
e^{i\omega t}
$$
です。
いろいろな $\omega$ で回っているこの「小さな円運動」を、重ね合わせていくと元の信号になる、というイメージです。
フーリエ変換をすると、
- 時間とともに変化する信号 $f(t)$ が
- 角周波数 $\omega$ に対する 複素数 $F(\omega)$ の集まりに変換されます。
この複素数 $F(\omega)$ の中身は、
- 絶対値（大きさ）：その周波数の振幅
- 偏角（角度）：その周波数の位相
という意味を持っています。
ここで効いているのが、まさに 複素数の表現力です。
- 実部：cos 成分
- 虚部：sin 成分
- 大きさ：その周波数の強さ
- 角度：タイミングのずれ（位相）
という情報を、ひとつの複素数で表現できることで、
「信号を“周波数ごとの振幅と位相”で見直す」
ことが可能になります。
ここまでが、フーリエ変換の「直感」編です。
この先の話として、ラプラス変換との関係にも少しだけ触れておきます。
余談：ラプラス変換とフーリエ変換 ― 微分積分を「代数」に変えるという共通点
ここまで読んで、
「微分積分を代数的に扱う」といえば、むしろラプラス変換のイメージが強い
という人もいるかもしれません。
制御工学や回路の分野では、
- 微分方程式をラプラス変換する
- 変数 $s$ を使った代数方程式に落とす
- 伝達関数 $G(s)$ として整理する
という流れが定番になっているので、
「微分積分を代数的に扱う ＝ ラプラス変換」
という理解でも、実務的にはあまり困りません。
ただ、ここまで見てきたように、実は フーリエ変換も条件付きで同じことをやっています。
フーリエ変換でも微分は「掛け算」になる
すでに出てきたように、
$$
\frac{d}{dt} e^{i\omega t} = i\omega e^{i\omega t}
$$
という性質があるので、
- 微分方程式をフーリエ変換すると
- 周波数領域では「$i\omega$ を掛ける」だけ
- → ここでも 微分が代数的な演算に変わっている
という構造になっています。
もちろん、フーリエ変換が適用できるためには
- 可積分であること
- ある種の意味で「十分おとなしい関数」であること
などの条件は必要ですが、
「微分積分を、周波数領域でただの掛け算にしてしまう」
という発想そのものは、ラプラス変換と共通です。
「ラプラス変換だけの特技」ではなく、フーリエ側の性質の延長線上にある
ラプラス変換はよく
- 微分方程式を解くための道具
- 初期値問題を扱うための道具
として紹介されますが、その核になっているのは
「指数関数を固有関数にして、微分演算子を“単なる $s$ の掛け算”にしてしまう」
という考え方です。
微分演算子の固有関数としては $e^{st}$ を使いますが、
ラプラス変換そのものの カーネル（核になる関数） は
$$
e^{-st}
$$
です。ラプラス変換の定義は
$$
\mathcal{L}{f(t)}(s) = \int_0^{\infty} f(t) e^{-st} \, dt
$$
のような形になっています。
ここで $s = \sigma + i\omega$ と分解すると、
$$
e^{-st} = e^{-(\sigma + i\omega)t}
= e^{-\sigma t} \cdot e^{-i\omega t}
$$
となり、
- $e^{-\sigma t}$：時間とともに小さくなっていく 減衰 の成分
- $e^{-i\omega t}$：角速度 $\omega$ で回転する フーリエ的な成分
の掛け合わせだと見ることができます。
つまり、基本パーツの違いで見ると、
- フーリエ変換：$e^{\pm i\omega t}$（純粋な回転）を基本パーツにする
- ラプラス変換：$e^{-\sigma t} e^{\pm i\omega t}$（減衰付きの回転）を基本パーツにする
という関係になっています。
言い換えると、
「フーリエで見た $e^{i\omega t}$ の性質を、
現実の“減衰する系”にまで拡張したのがラプラス変換」
という見方ができます。
- フーリエ → 純粋な周期・回転の世界
- ラプラス → 減衰や初期値も含んだ、より一般的な時間応答の世界
という位置づけで、どちらも
「微分という面倒な演算を、“$s$ や $i\omega$” の掛け算に変えてくれる座標変換」
だと理解しておくと、フーリエとラプラスの関係がかなりスッキリ見えてきます。
※ちょっとだけ歴史とトリビアの余談
数学的には、ラプラス変換は$s=\sigma+i\omega$のうち$\sigma=0$の線(虚軸)を見ると「虚軸上に制限するとフーリエ変換になる」という意味で、フーリエ変換の一般化とみなせます。ただし歴史的には、ラプラス変換的なアイデアとフーリエの熱方程式の研究は別々に発展してきたとされていて、「フーリエを拡張しようとしてラプラス変換が発明された」というきれいなストーリーではありません。
オイラーの公式があったおかげで、どちらも「複素指数 × 積分」というよく似た形で書けるようになった、というのが現代から見た整理だと考えると雰囲気がつかみやすいと思います。この文章では、あくまで現代的な見方としての“一般化”だと理解してもらえれば十分です。
まとめ：虚数・複素数・フーリエ変換がつながると見えるもの
ここまでの内容をざっくり整理すると、次のようになります。
- 自然数・整数の世界では「増減」や「行ったり来たり」は表せるが、なめらかな「周期」や「回転」を扱うには 1 本の軸では足りない。
- そこで直交するもう 1 本の軸（虚数軸）を導入し、複素平面の上で「i を掛ける = 90度の回転」とみなすことで、回転や位相の変化を自然に表現できるようになる。
- sin, cos は「微分すると位相がずれるだけ」という、周期と微分に強い関数であり、周期現象のモデルとして非常に相性が良い。
- オイラーの公式 $e^{i\theta} = \cos\theta + i\sin\theta$ によって、三角関数を複素平面に“閉じ込める”ことで、$\displaystyle\frac{d}{dt}e^{i\omega t} = i\omega e^{i\omega t}$ のように、微分が単純な掛け算に変わる。
- フーリエ変換は、信号を「いろいろな速さの回転（波）」の足し合わせとして見る変換であり、その“回転の基本パーツ”として $e^{i\omega t}$（複素指数）が使われる。その結果、角周波数ごとの振幅と位相を、複素数として一括で扱える。
- ラプラス変換は、そのフーリエ的な発想をさらに拡張し、減衰や成長を含んだ系に対しても、微分を「$s$ の掛け算」に落とせるようにした道具と見なせる。
こうして眺めてみると、虚数・複素数は
「$\sqrt{-1}$ というよく分からない数」ではなく、
「回転・周期・位相といった現象を、微分・積分と相性よく扱うための座標拡張」
だと捉え直すことができます。
ここではフーリエ変換の「直感」と、ラプラス変換との関係をざっくり眺めるところまでにとどめましたが、この先にはさらに、
- 畳み込みとフーリエ変換の関係（畳み込みが掛け算に変わる話）
- ラプラス変換と伝達関数、安定性解析とのつながり
- 制御・信号処理・機械学習の中での応用
なども広がっています。
虚数やフーリエ変換、ラプラス変換に苦手意識がある場合でも、
「結局のところ、回転と周期をうまく扱うための道具なんだ」
という視点を一つ持っておくと、
今後ほかの分野で複素数や変換が出てきたときにも、少し見え方が変わってくるはずです。
- 虚数・複素数は「√-1という謎の数」ではなく、回転と周期・位相を扱うために数直線を2次元に拡張した座標。
- sin, cos とオイラーの公式で三角関数を複素平面に閉じ込めることで、微分積分が「iω を掛ける」という代数的な操作に変わる。
- フーリエ変換とラプラス変換はどちらも、信号や微分方程式を「回転（＋減衰）」の足し合わせとして見直し、面倒な微分を単なる掛け算にしてくれる道具。
よくある質問（FAQ）
Q1. 虚数って「実在しない数」なんですか？
A. 物理的なモノとしてあるわけではありませんが、回転・周期・位相といった現象を表す「座標」の拡張として使われる、便利な数学的な道具です。
Q2. なぜフーリエ変換には必ず i（虚数）が出てくるのですか？
A. フーリエ変換は「回転する波」を基本パーツとして信号を分解するための道具です。回転を表すには複素数がいちばん自然なので、式の中に i が現れます。
Q3. ラプラス変換とフーリエ変換はどう使い分ければいいですか？
A. 純粋な周期・周波数特性を見たいときはフーリエ変換、減衰や初期値を含む時間応答まで扱いたいときはラプラス変換、という使い分けが典型的です。
Q4. この記事を読むのにどのくらいの数学知識が必要ですか？
A. 高校レベルの三角関数と、複素数の「実部・虚部」程度が分かっていれば十分読める内容を目指しています。厳密な証明は扱っていません。微分やフーリエ変換の式がちゃんと分からなくても、“回転と周期の話なんだな”という雰囲気だけ掴んでもらえれば十分です。
その他のエッセイはこちら
ニュートン先生の虚数講義 (ニュートン先生シリーズ)
役に立ち、美しい はじめての虚数
増補改訂版 小学校6年分の算数が教えられるほどよくわかる
ふたたびの高校数学
高校数学でわかるフーリエ変換 : フーリエ級数からラプラス変換まで (ブルーバックス)
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす (ブルーバックス)
コメント