はじめに
Youtubeチャンネルの方の
視聴者さんからのリクエストである、
「小学生向けの動画シリーズ」のブログ版。
旅人算から始まり、グラフや交点算出。
動画
動画による解説はこちら。
類似動画シリーズ
おしながき
今回の内容になる。
- 小学生向け:旅人算
- 中学生向け:グラフ
- 高校生向け:交点算出
グラフは、なんとなくやりたいことは思いつくかもしれない。
それぞれはかなり密接な関係。
小学生向け:旅人算
まずは旅人算。
とりあえず問題を出してみる。
たろうくんとつよしくんは、ある朝、同じ家から徒歩で出発しました。
- たろうくんは 毎分80メートル の速さで出発しました。
- その15分後に、つよしくんが 毎分100メートル の速さで同じ道を追いかけて出発しました。
さて、つよしくんがたろうくんに追いつくのは、出発してから何分後でしょうか?
懐かしい問題である。
たろうくんは15分くらい待ってやって一緒に出発すれば良くね?
というツッコミは旅人算あるある・・・。
仮につよしくんがたろうくんに追いついても、その瞬間、たろうくんは少し先に進むから、つよしくんは一生追いつけない!
というのはアキレスとカメのパラドックス。
最初に必要なのは、つよしくんが出発する段階で、たろうくんがどのくらい進んだか。
この問題で良く直面するのが、
毎分80メートルって速度の情報と15分という時間の情報はあるが、距離の情報がない!
なのだが、
当然、速度と時間が分かれば距離が出る。
ここで出てくるのが「みはじ」
こんな感じの絵になる。
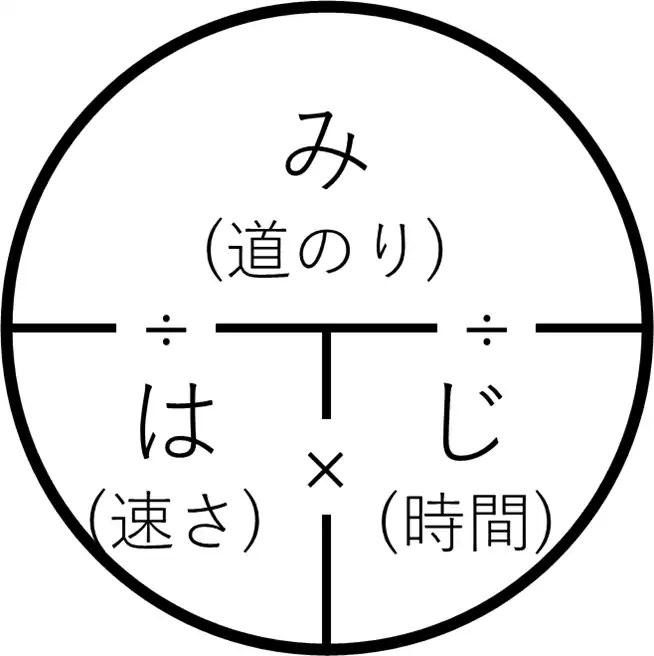
求めたいところを手で隠すと、それを求める式が分かるってもの。
今回知りたいのは距離。つまり道のりだから、みを隠す。
そうすると、速さと時間をかければ求められることがわかる。
しかし、「みはじ」の利用に対してって否定的な人たちもいる。
速度、時間、距離の関係性を隠蔽してしまって、物理学や微分積分を学ぶ際に混乱が起きると言われている。
まぁ、私としてはそのようなリスクがあることを知ったうえで使用するのは問題無いと思っている。
便利な暗記ツールであることは間違いないわけなので、リスクを回避しつつ上手く使うというのが一番良い。
15分後にたろうくんはどこにいるかと言うと、
毎分80メートル × 15分 = 1200メートル
この距離をつよしくんは埋めないといけない。
つよしくんは毎分100メートルの速さで歩くわけだから、毎分20メートルずつ差が縮まる。
1200メートル ÷ 毎分20メートル = 60分
よって、60分後に追いつく。
問題としては問うては居ないが、2人とも6キロメートルは歩いてる。
ここまで考えるとどこに向かったのか気になってくる・・・。
このように問題で問われていないところも考えるクセが付いていると、
速度、時間、距離の関係を明確に把握できるようになると思う。
中学生向け:グラフ
たろうくんとつよしくんは、ある朝、同じ家から徒歩で出発しました。
- たろうくんは 毎分80メートル の速さで出発しました。
- その15分後に、つよしくんが 毎分100メートル の速さで同じ道を追いかけて出発しました。
さて、つよしくんがたろうくんに追いつくのは、出発してから何分後でしょうか?
次はグラフ。
たろうくんとつよしくんの移動をグラフで表現する。
ここで問題になるのが、何をグラフで表現するか。
この場合は、何が変化するかに着目して、それを縦軸に置くという考え方になる。
答えは移動距離ですね。
縦軸を移動距離、横軸を時間にすると良い。
たろうくんを原点からスタートして、1分毎に80メートル増加する直線を引く。
つよしくんは横軸の15分からスタートして、1分毎に100メートル増加する直線を引く。
そして、その直線が交差する点を求める。
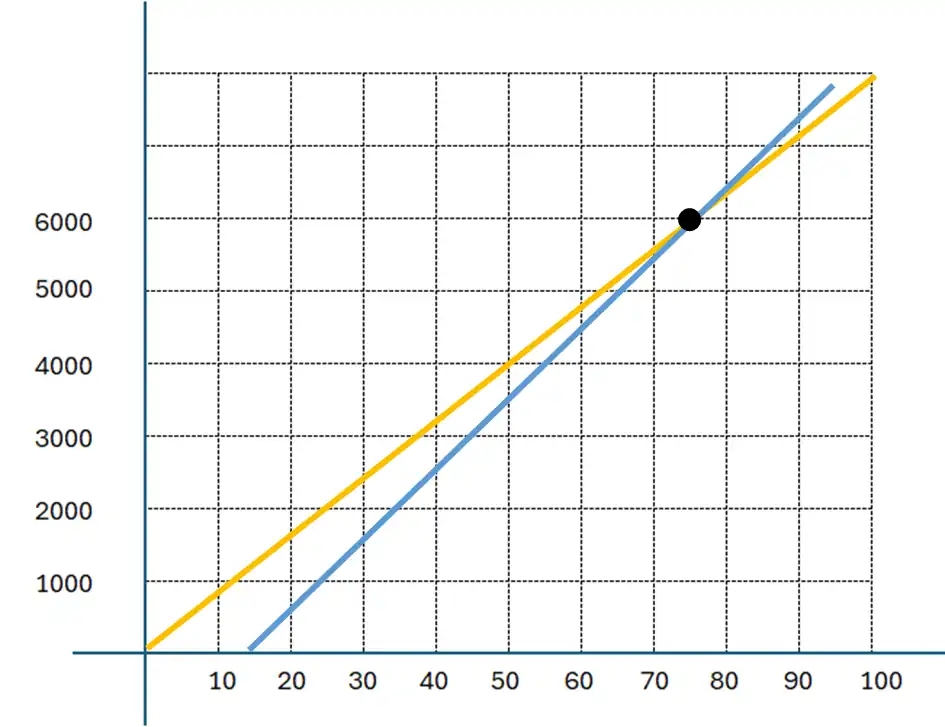
交差するのは縦軸が6000メートルで、横軸が75分のところ。
先ほどの答えは60分に対して、グラフでの答えは75分。
間違っているようにも見えるが、
問題文で問うてるのは、つよしくんが出発してからの時間。
75分から15分を引いて60分ってことなにであってる。
地味に読解力が問われるのもこの手の問題あるある。
グラフを使うとイメージがわきやすい。
小学生もこの方法で解いてみると良い。
高校生向け:交点算出
たろうくんとつよしくんは、ある朝、同じ家から徒歩で出発しました。
- たろうくんは 毎分80メートル の速さで出発しました。
- その15分後に、つよしくんが 毎分100メートル の速さで同じ道を追いかけて出発しました。
さて、つよしくんがたろうくんに追いつくのは、出発してから何分後でしょうか?
次は交点算出。
つまりは、さっきのグラフの交点を算出する方法があるってことになる。
交点と言えば連立方程式。
問題は、方程式を2つ用意することになるのだが、
どんな方程式を使えば良いかが悩みどころになり易い。
答えは、先ほどのグラフの一次方程式を使えばOK。
縦軸の距離をyとして、横軸の時間をxとする。
そうすると、2人の移動距離を示す方程式は以下になる。
たろうくんの式:
$$
y=80x
$$
つよしくんの式:
$$
y=100(x-15)
$$
つよしくんの式が一見すると連立方程式で使え無さそうな式にみえるが、
これは普通にこんな感じでカッコを取って展開すれば良い。
$$
y=100x-1500
$$
そうするとこんな感じで解ける。
$$
\begin{eqnarray}
80x&=&100x-1500\\
-20x&=&-1500\\
x&=&75\\
y&=&80×75=6000
\end{eqnarray}
$$
つまり、6000メートルの地点で75分後。
グラフで求めたものと同じ結果になった。
そして、連立方程式で求められるということは、逆行列でも求められる。
逆行列は、このシリーズの第1回目のつるかめ算のときにもやった。
連立方程式を行列で表現するとこんな感じ。
$$
\begin{cases}
80x-y&=&0\\
100x-y&=&1500
\end{cases}
$$
$$
\begin{bmatrix}
80&-1\\
100&-1\\
\end{bmatrix}
\begin{bmatrix}
x\\y
\end{bmatrix}=
\begin{bmatrix}
0\\1500
\end{bmatrix}
$$
行列を左辺から右辺に移動する際に逆行列になる。
$$
\begin{bmatrix}
x\\y
\end{bmatrix}=
\begin{bmatrix}
80&-1\\
100&-1\\
\end{bmatrix}^{-1}
\begin{bmatrix}
0\\1500
\end{bmatrix}
$$
逆行列はこんな感じで求める。
$$
\begin{eqnarray}
&&\frac{1}{80\times(-1)-100\times(-1)}
\begin{bmatrix}
-1&1\\
-100&80\\
\end{bmatrix}
\begin{bmatrix}
0\\1500
\end{bmatrix}
\&=&\frac{1}{20}
\begin{bmatrix}
-1&1\\
-100&80\\
\end{bmatrix}
\begin{bmatrix}
0\\1500
\end{bmatrix}
\\&=&
\begin{bmatrix}
-0.05&0.05\\
-5&4\
\end{bmatrix}
\begin{bmatrix}
0\\1500
\end{bmatrix}
\\&=&
\begin{bmatrix}
-0.05\times 0+0.05\times 1500\\
-5\times 0+4\times 1500\\
\end{bmatrix}
\\&=&
\begin{bmatrix}
75\\6000
\end{bmatrix}
\end{eqnarray}
$$
時間が75分で、距離が6000メートルだからあってる。
ちなみにPythonのNumPyを使用するとこんな感じで解ける。
import numpy as np
# 係数行列 A と 定数ベクトル B の定義
A = np.array([[80, -1],
[100, -1]])
B = np.array([0, 1500])
# 逆行列の計算
A_inv = np.linalg.inv(A)
# 解の計算(x, y)
solution = np.dot(A_inv, B)
x, y = solution
print(f"Solution:\n x = {x} minutes\n y = {y} meters")Solution:
x = 75.00000000000001 minutes
y = 6000.000000000001 metersと一撃。
なんだかんだで逆行列にはお世話になることが多い。
行列とか意味不明ってイメージを持つことが多いかもしれないが、便利さの方が目立ってる。
つまり、行列も単なる便利ツールでしかないってことになる。
まとめ
- 旅人算を使って速さ・時間・距離の関係を学んだ。
- グラフで2人の移動を可視化し、交点から追いつく時間と距離を視覚的に理解。
- 連立方程式と逆行列を使って交点を代数的に算出し、数学的な解法のつながりを体験。
中学受験 ミラクル算数 特殊算
数学ガールの秘密ノート/式とグラフ
数学ガールの秘密ノート/行列が描くもの





コメント