その他のエッセイはこちら
はじめに
筆者の立場と本稿の視点
筆者は電気工学を専門とし、情報工学の設計思想やOOPの形式体系については専門的な教育を受けていない。そのため本稿では、電気工学的・数理構造的な視点からソフトウェア設計の抽象性を再解釈するという立場を取っている。情報工学における慣習的な枠組みとは異なる見方を提示する可能性があるが、それゆえに新たな視点を提供できればと考えている。
対象読者と前提知識
本稿は、情報工学・電気工学・機械学習分野に関心を持つ大学院生や実務エンジニアを対象とする。以下のような基礎的知識を有している読者を想定する:
- Python等による基本的なプログラミング経験
- 線形代数の初歩(ベクトル、行列、内積、線形写像の概念)
- 機械学習の枠組みにおけるテンソル演算やAttentionの基礎的理解
- 必須ではないが、関数型プログラミングや型理論に片足を突っ込んでいる程度の抽象性への耐性があると望ましい
必要に応じて、本文中では重要な概念の簡潔な補足も行う。
本稿を読み進める上で最低限必要となる線形代数の基礎事項については、末尾に補足を設けている。必要に応じて参照されたい。
問題意識と背景
オブジェクト指向(Object-Oriented Programming, OOP)は、ソフトウェア設計における主流パラダイムとして長年にわたり用いられてきた。クラス、継承、ポリモーフィズムといった概念は、複雑な構造を整理・抽象化する手段として広く受け入れられている。
しかし近年、Transformer や Attention をはじめとする深層学習モデルの台頭により、ソフトウェア構造の記述パラダイムはより関数的・行列的・動的なものへと移行しつつある。これにより、OOP がもたらしてきた構造的抽象性の限界や、他の抽象体系(関数型、テンソル計算、カテゴリ的構造など)との統合的視座の必要性が浮かび上がってきた。
本稿の目的と問い
本稿の目的は、OOPの主要な設計要素(状態、継承、ポリモーフィズム)を、線形代数的構造に基づいて再解釈することである。これは、単にOOPを線形代数で置き換えることではなく、両者が共通して持つ構造的対応関係を明らかにし、さらにそれがAttentionやTransformerのような現代的なパラダイムと地続きであることを示す試みである。
これまでにも、OOPを状態遷移系や有限オートマトン、あるいはモデル駆動アーキテクチャと結びつける試みはあったが、多くは「設計言語」や「仕様の記述」の範疇に留まり、数理構造としての連続性(特に線形変換・テンソル操作との共通性)には踏み込んでこなかった。
本稿の新規性は、OOPの内部構造を関数合成と行列演算の形式性に基づいて捉え直すことで、OOP・線形代数・関数型プログラミング(FP)・Attentionといった異なる抽象体系が、操作ではなく「構造」の次元で連続していることを示す点にある。
その出発点として、以下の問いを掲げる:
「オブジェクトとは、線形代数的に変換行列として捉えられるのではないか?」
この問いは単なる思考実験にとどまらず、AIモデルの設計、並列処理の形式化、FPとの接続といった応用的な設計視座の再構成にもつながる可能性を持っている。
本稿ではこの問いを軸に、オブジェクトの再定義を試みながら、継承、ポリモーフィズム、非線形変換、Attention、さらに大規模言語モデル(LLM)との構造的連関について、順を追って考察していく。
オブジェクト = 変換行列:状態遷移モデルとしての再解釈
オブジェクト指向プログラミング(OOP)は、もともと物理シミュレーションの文脈で発展した設計思想である。物体が状態(位置、速度など)を持ち、時間とともに変化する様子を記述するために、オブジェクトという概念が導入された。ここでの「状態」はベクトル量であり、「振る舞い」はそれに作用する変換操作である。
この構造は、線形代数における状態遷移モデルと一致する。すなわち、ある時刻の状態ベクトル $x_t$に対して、変換行列 $A$ を作用させることで次の状態 $x_{t+1}$ を得る:
$$
\boldsymbol{x}_{t+1} = A \cdot \boldsymbol{x}_t
$$
※この式は、行列Aにベクトル $x_t$ を掛けることで、次の状態 $x_{t+1}$ を得る「線形変換」を表している。これは、物理システムやニューラルネットワークの基本構造でもある。
※この式は、離散時間状態空間モデルの簡略化形としても捉えることができる。通常の状態空間モデルでは、外部入力 $u_t$ を含む項 $Bu_t$ が加わるが、本稿ではオブジェクト内部の状態変化に焦点を当てるため、入力項を省略し、純粋な状態遷移のみを記述している。
離散状態空間モデル:
$$
\begin{eqnarray}
\boldsymbol{x}_{t+1}=A\boldsymbol{x}_t+B\boldsymbol{u}_t\\
\boldsymbol{y}_t=C\boldsymbol{x}_t+D\boldsymbol{u}_t
\end{eqnarray}
$$
※この式は、ニューラルネットワークの基本構造にも対応している。ニューラルネットワークでは、各レイヤーにおける出力は、前のレイヤーの状態ベクトル $x_t$ に対して重み行列 $A$ を掛けることで得られる。これは、線形変換による状態更新を表しており、活性化関数を加えることで次のような一般的なニューラルネットワークの層構造となる:
$$
\boldsymbol{x}_{t+1}=f(A\cdot \boldsymbol{x}_t)
$$
ここで $f$ は ReLU や sigmoid などの非線形関数であり、状態空間モデルにおける線形変換と非線形変換の組み合わせが、ニューラルネットワークの基本構造と一致することがわかる。
このとき、オブジェクトは「状態ベクトルとそれに作用する変換行列の組」として捉えることができる。これは、OOPにおける「プロパティ(属性)」と「メソッド(振る舞い)」の構造と対応している。
さらに、現代の計算環境では、単一の状態ベクトルに対する変換だけでなく、複数の状態ベクトルに対する一括変換(バッチ処理)が重要となる。たとえば、次のように複数の入力ベクトルを列方向に並べた行列 $X^{(n)}$ に対して、同一の変換行列 $A$ を適用することで、並列的に出力を得ることができる:
$$
Y^{(n)} = A \cdot X^{(n)},\ \ X\in\mathbb{R}^{d\times n}, Y\in\mathbb{R}^{d^\prime\times n},
$$
※ 上記式を行列表現にすると以下になる:
$$
\begin{bmatrix}
y_{11}&\dots&y_{1n}\\
\vdots&\ddots&\vdots\\
y_{d^\prime1}&\dots&y_{d^\prime n}\\
\end{bmatrix}=
\begin{bmatrix}
a_{11}&\dots&a_{1d}\\
\vdots&\ddots&\vdots\\
a_{d^\prime1}&\dots&a_{d^\prime d}\\
\end{bmatrix}
\begin{bmatrix}
x_{11}&\dots&x_{1n}\\
\vdots&\ddots&\vdots\\
x_{d1}&\dots&x_{dn}\\
\end{bmatrix}
$$
※ (d=3,d^\prime=2,n=4)の場合だと以下になる:
$$
\begin{bmatrix}
5&-1&5&11\\
-2&-2&1&-1
\end{bmatrix}=
\begin{bmatrix}
1&2&3\\
0&-1&1
\end{bmatrix}
\begin{bmatrix}
1&0&2&-1\\
2&1&0&3\\
0&-1&1&2
\end{bmatrix}
$$
ここでの $n$ はバッチサイズと呼ばれ、同時に処理されるデータの数を表す。これは、GPUなどの並列計算資源を最大限に活用するための単位であり、ディープラーニングや大規模データ処理において不可欠な概念である。各列ベクトル(個々の入力)に対する演算が独立しているため、スケーラブルかつ効率的な処理が可能となる。
バッチサイズ(batch size)とは、機械学習や並列処理において一度に処理されるデータの個数を指す。たとえば、画像分類タスクでバッチサイズが32であれば、32枚の画像が同時にネットワークに入力され、同じ重み行列に対して並列に処理される。
線形代数的には、各入力ベクトルを列として並べた行列 $X\in \mathbb{R}^{d\times n}$ に対して、変換行列Aを一括で適用する操作に相当する。GPUなどの並列計算資源を活用する上で、バッチ処理は計算効率とメモリ最適化の鍵となる。
加えて、変換行列の各「行」に対応する演算もまた独立しており、出力ベクトルの各成分は入力ベクトルとの内積によって個別に計算される:
$$
y_i=a_j\cdot x\ \ (j=1,2,\dots,d^\prime)
$$
ここで $a_j$ は変換行列Aの第j行であり、各 $y_i$ の計算は他の出力成分と独立している。これは、出力次元ごとの処理が並列化可能であることを意味し、ニューラルネットワークのフォワードパスなどにおいて重要な性質である。
このように、入力方向(列)と出力方向(行)の両面で並列性が存在することは、線形代数的モデルが高いスケーラビリティを持つ理由の一つであり、オブジェクト指向的な設計においても有用な視点となる。
オブジェクトを「状態遷移を担う変換行列」として捉えることで、物理的直感・数理的記述・並列処理の効率性が統合され、現代のソフトウェア設計における抽象化の強力な枠組みとなる。
例:オブジェクトを線形変換として表現する
import numpy as np
# 「オブジェクト」としての変換行列(例:2次元空間の回転)
class LinearObject:
def __init__(self, matrix):
self.matrix = matrix # 変換行列
def apply(self, vector):
return self.matrix @ vector # 線形変換を適用
# 例:2次元空間におけるオブジェクト(回転行列)による線形変換の適用
theta = np.pi / 4
rotation_matrix = np.array([
[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]
])
# オブジェクトを生成
rotator = LinearObject(rotation_matrix)
# 入力ベクトル
x = np.array([[1], [0]])
# 出力ベクトル(回転後)
y = rotator.apply(x)
print("入力ベクトル:\n", x)
print("変換後ベクトル:\n", y)入力ベクトル:
[[1]
[0]]
変換後ベクトル:
[[0.70710678]
[0.70710678]]継承・ポリモーフィズム = 行列の差し替え・切り替え
オブジェクト指向の中核にある継承やポリモーフィズムも、線形代数的に解釈できる。
継承:変換行列の拡張
継承は、ソフトウェア設計において「子クラスが親クラスの構造や振る舞いを引き継ぎつつ、必要に応じて変更や拡張を行う」という概念として理解されている。これを線形代数的に表現するならば、以下の関係式が直観的に用いられることが多い。
$$
A_{child} = A_{parent} + \Delta A
$$
ここで $\Delta A$ は、親クラスからの差分としての追加的な変換成分を表す。
だしこのときの「+」は、 $A_{parent}$ を完全に上書きする操作ではなく、構造的に保持したまま $\Delta A$ を加えるような意味合いを持つ。すなわち、継承とは「ベースとなる変換行列 $A_{parent}$ を残しつつ、そこに差分変換 $\Delta A$ を付加する」ような構造の拡張操作として捉えるべきであり、単純な線形加算や置換操作とは区別される必要がある。
この視点に立つと、子クラスは親クラスの変換を部分的に再利用しながら、独自の変換(振る舞いや状態)を追加していることになる。変換行列としてのオブジェクトの再解釈は、こうした拡張可能な構造体としての側面を明示的に捉えることに寄与する。
例:継承 = 行列の差分
import numpy as np
# 「オブジェクト」としての変換行列
class LinearObject:
def __init__(self, matrix):
self.matrix = matrix
def apply(self, vector):
return self.matrix @ vector # Apply linear transformation
# 親クラスの変換行列(単位行列)
parent_matrix = np.eye(2)
# 子クラスの差分行列(スケーリング)
delta_matrix = np.array([
[2, 0],
[0, 1]
])
# 入力ベクトル
x = np.array([[1], [0]])
# 子クラスの行列 = 親 + 差分
child_matrix = parent_matrix + delta_matrix
# 子オブジェクト
scaler = LinearObject(child_matrix)
# 同じ入力に対して異なる出力
print("親オブジェクト:\n", LinearObject(parent_matrix).apply(x))
print("子オブジェクト:\n", scaler.apply(x))親オブジェクト:
[[1.]
[0.]]
子オブジェクト:
[[3.]
[0.]]ポリモーフィズム:行列の切り替え
ポリモーフィズムは、同一の入力に対して異なる変換行列を適用することで、異なる出力を得る構造である:
$$
y_1 = A_1 \cdot x,\quad y_2 = A_2 \cdot x
$$
これは、動的ディスパッチの数理的表現と捉えることができ、実行時に適切な変換行列を選択することで柔軟性と抽象性を両立した設計が可能となる。
例:ポリモーフィズム = 行列の切り替え
# 「オブジェクト」としての変換行列
class LinearObject:
def __init__(self, matrix):
self.matrix = matrix # 変換行列
def apply(self, vector):
return self.matrix @ vector # 線形変換を適用
# 2つの異なる変換行列
A1 = np.array([[1, 2], [0, 1]])
A2 = np.array([[0, 1], [-1, 0]])
# 入力ベクトル
x = np.array([[1], [0]])
# 同じ入力に対して異なるオブジェクトを適用
obj1 = LinearObject(A1)
obj2 = LinearObject(A2)
print("A1による変換:\n", obj1.apply(x))
print("A2による変換:\n", obj2.apply(x))A1による変換:
[[1]
[0]]
A2による変換:
[[ 0]
[-1]]非線形関数 = 条件分岐の抽象化
線形変換のみでは表現できない処理も、非線形関数を挿入することで対応可能となる:
$$
Y = f(A \cdot X)
$$
この構造は、ソフトウェアにおける if や switch のような条件分岐を、連続的な関数として抽象化することを可能にする。
たとえば、ReLU(Rectified Linear Unit)関数:
$$
f(x) = \max(0, x)
$$
※ReLU(Rectified Linear Unit)は、入力が0以下なら0、それ以外はそのまま返す関数。ニューラルネットワークでよく使われ、条件分岐のような役割を果たす。
これは、条件分岐を滑らかに連続化したものと見なすことができる。sigmoidやtanhなども同様に、非線形な振る舞いを連続的に表現するための関数である。
このような非線形関数の導入により、複雑な状態遷移や条件分岐を数式として一貫して扱うことが可能となり、設計の明快さと解析可能性が向上する。
例:if文による条件分岐 vs ReLU関数
import numpy as np
import matplotlib.pyplot as plt
# 明示的な条件分岐(if文)
def step_function(x):
return np.array([1 if xi > 0 else 0 for xi in x])
# 非線形関数:ReLU(連続的な条件分岐の抽象化)
def relu(x):
return np.maximum(0, x)
# 非線形関数:sigmoid(より滑らかな分岐)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 入力ベクトル
x = np.linspace(-5, 5, 200)
# 出力
y_step = step_function(x)
y_relu = relu(x)
y_sigmoid = sigmoid(x)
# 可視化
plt.figure(figsize=(10, 6))
plt.plot(x, y_step, label='Conditional branching by if statement(step)', linestyle='--')
plt.plot(x, y_relu, label='ReLU (nonlinear function)')
plt.plot(x, y_sigmoid, label='Sigmoid (smooth bifurcation)')
plt.title("Comparison of conditional branches and nonlinear functions")
plt.xlabel("x")
plt.ylabel("Outpu")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()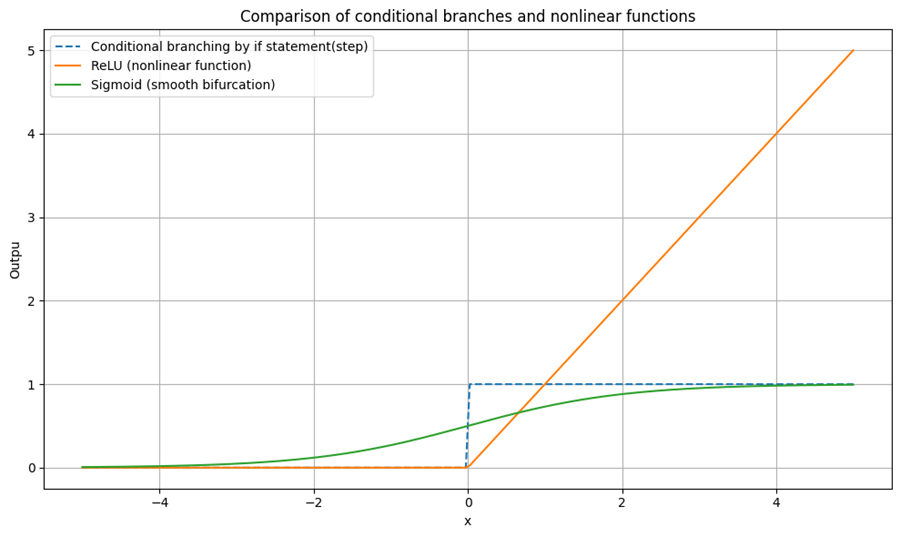
関数型プログラミングとの接点
関数型プログラミング(Functional Programming, FP)は、状態を持たない純粋関数を中心に構成される。この構造は、線形代数における「入力 → 出力」の写像と非常に近い。
高階関数と行列演算
関数型では、関数を引数に取る、あるいは関数を返す「高階関数」が基本的な構成要素となる。これは、行列を操作する関数やテンソル演算と構造的に一致する。
関数合成:
$$
f(x)=g(h(x)) \Leftrightarrow A\cdot(B\cdot x)=(A\cdot B)\cdot x
$$
この対応は、関数型の抽象的な処理の流れを線形代数的に明確に表現するものである。
例:高階関数の例(関数合成)
import numpy as np
import matplotlib.pyplot as plt
# --- 高階関数の例(関数合成) ---
def g(x):
return x + 3
def f(x):
return 2 * x + 5
# アフィン変換 g(x) = x + 3
A1 = np.array([[1]])
b1 = np.array([[3]])
# アフィン変換 f(x) = 2x + 5
A2 = np.array([[2]])
b2 = np.array([[5]])
# 拡張行列の構築(同次座標系)
A1_ext = np.hstack([A1, b1]) # [A1 | b1]
A1_ext = np.vstack([A1_ext, [0, 1]]) # 下に [0, 1] を追加
A2_ext = np.hstack([A2, b2]) # [A2 | b2]
A2_ext = np.vstack([A2_ext, [0, 1]]) # 下に [0, 1] を追加
# 合成変換行列 A_comp = A2_ext @ A1_ext
A_comp = A2_ext @ A1_ext
# 入力 x の範囲
x_vals = np.linspace(-10, 10, 200)
x_ext = np.vstack([x_vals, np.ones_like(x_vals)]) # 拡張ベクトル [x; 1]
# 各関数の出力
y_g = f(x_vals)
y_f = g(x_vals)
y_fg = f(g(x_vals))
y_comp = (A_comp @ x_ext)[0] # 合成行列による出力
# グラフ描画
plt.figure(figsize=(10, 6))
plt.plot(x_vals, y_f, label='f(x) = 2x + 5', color='blue')
plt.plot(x_vals, y_g, label='g(x) = x + 3', color='orange')
plt.plot(x_vals, y_fg, label='f(g(x)) = 2(x + 3) + 5', linestyle='--', color='green')
plt.plot(x_vals, y_comp, label='Composition by augmented matrix', linestyle=':', color='red')
plt.title("Comparison of affine transformation synthesis and function synthesis")
plt.xlabel("x")
plt.ylabel("output ")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()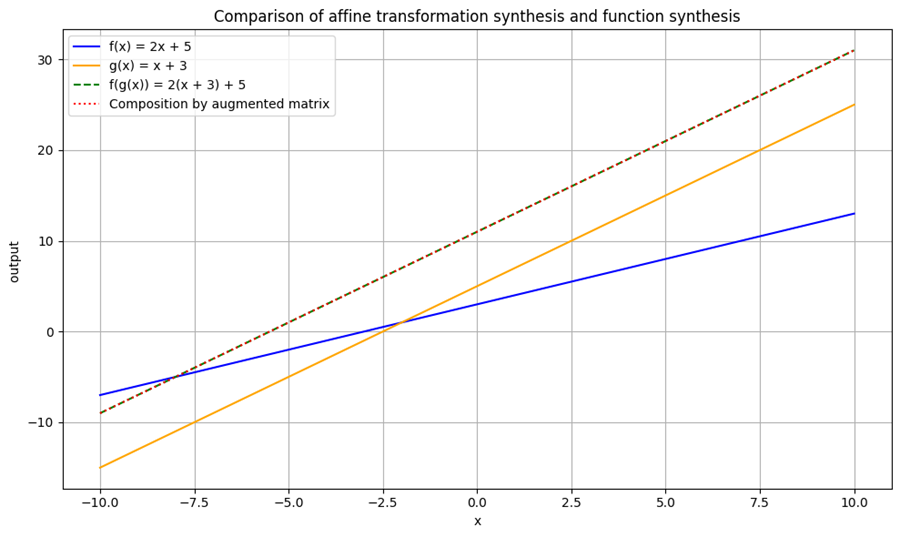
条件分岐の線形的表現と関数的抽象
関数型プログラミングでは、状態を持たず、条件分岐も関数として抽象化することが推奨される。これは、線形代数的な処理モデルと親和性が高い。
たとえば、従来の if 文による条件分岐は、明示的な制御構造であり、処理の流れを分岐させる。一方、ニューラルネットワークでは、ReLU や sigmoid のような非線形関数を用いて、条件分岐を連続的かつ微分可能な形で表現する。
このような非線形関数は、線形変換と組み合わせることで、複雑な振る舞いを滑らかに表現できる。さらに、関数型プログラミングにおけるパターンマッチや関数ディスパッチは、条件分岐の局所化と抽象化を実現し、ソフトウェアの構造を明快に保つ。
この構造は、以下のように整理できる:
| 概念 | ソフトウェア | 数理的対応 |
| 明示的条件分岐 | if, switch | 不連続な分岐 |
| 関数的抽象 | パターンマッチ、関数選択 | 関数合成、写像 |
| 数理的連続化 | ReLU, sigmoid | 非線形関数による滑らかな分岐 |
このように、条件分岐を関数として扱う発想は、線形代数的な処理モデルと関数型プログラミングの設計思想を橋渡しするものであり、抽象化の一形態として非常に有効である。
例:Haskellにおける階乗関数
factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n - 1)このように、条件分岐が関数定義の構造に組み込まれており、可読性と安全性が高まる。
import matplotlib.pyplot as plt
import numpy as np
# --- ① 従来型の条件分岐(if-else) ---
def factorial_if(n):
if n == 0:
return 1
else:
return n * factorial_if(n - 1)
# --- ② 関数型スタイル:辞書によるディスパッチ ---
def factorial_dispatch(n):
dispatch = {
0: lambda: 1 # n=0 の場合の処理
}
# 辞書に該当する関数があればそれを実行、なければ再帰的に計算
return dispatch.get(n, lambda: n * factorial_dispatch(n - 1))()
# --- ③ パターンマッチ(Python 3.10以降) ---
def factorial_match(n):
match n:
case 0:
return 1
case _: # その他の値
return n * factorial_match(n - 1)
# --- 入力と出力の準備 ---
inputs = list(range(6)) # 0〜5までの整数
outputs_if = [factorial_if(n) for n in inputs]
outputs_dispatch = [factorial_dispatch(n) for n in inputs]
outputs_match = [factorial_match(n) for n in inputs]
# --- グラフ描画 ---
plt.figure(figsize=(10, 6))
plt.plot(inputs, outputs_if, label='if-else(conventional type)', marker='o')
plt.plot(inputs, outputs_dispatch, label='dictionary dispatch (functional)', marker='s')
plt.plot(inputs, outputs_match, label='match-case (pattern match)', marker='^')
plt.title("Factorial calculations with different conditional branching styles")
plt.xlabel("input value n")
plt.ylabel("factorial(n)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()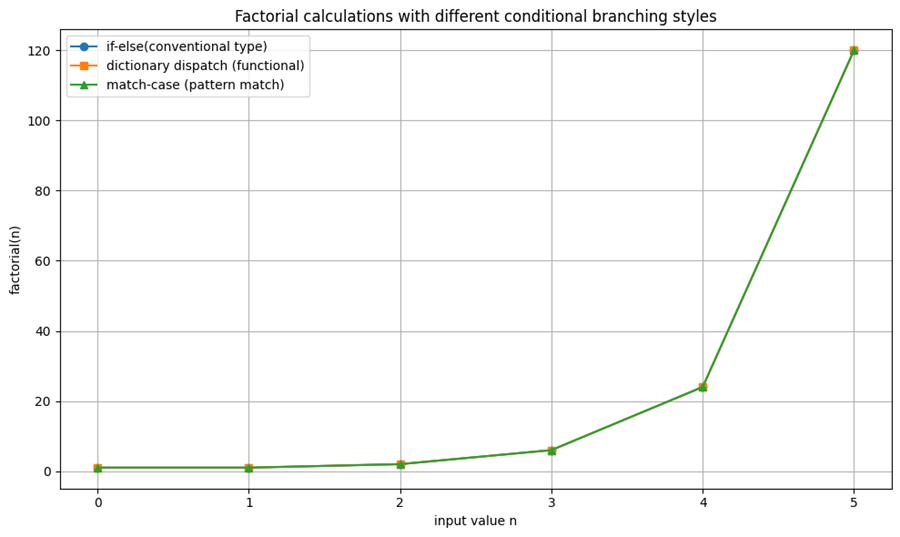
Attention機構の線形代数的解釈とオブジェクト指向的再構成
Attentionは、入力された情報の中から「どこに注目すべきか」を学習する仕組み。特に自然言語処理においては、文章中の単語同士の関係性を動的に捉えるために使われる。Transformerというモデルの中核をなす技術。
TransformerにおけるSelf-Attentionは、線形代数と非線形関数の組み合わせによって、情報の動的な関係性を計算する仕組みである。
Attentionの基本構造:
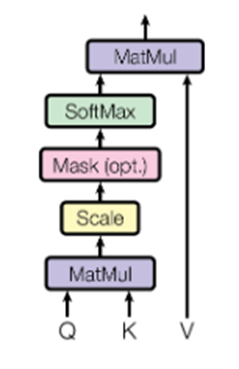
$$
\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\cdot V
$$
※この式は、Query(注目したい情報)とKey(識別子)の類似度を計算し、Value(実際の情報)を重み付きで合成する操作となる。自然言語処理で重要な役割を果たす。
これは入力間の関係性を重み付きで再構成する操作である。ここで、Query(Q)、Key(K)、Value(V)はそれぞれベクトルであり、入力トークンごとに生成される。
オブジェクトとしてのQuery/Key/Value
この構造は、オブジェクト指向的に以下のように解釈できる:
- Query:注目したい情報の特徴(目的)
- Key:各入力の識別子(属性)
- Value:実際に取り出す情報(状態)
QueryオブジェクトがKeyオブジェクト群に対して「どれに注目すべきか」を計算し、Valueから情報を抽出する。この構造は、オブジェクト間のメッセージパッシングや依存関係の動的構築と類似している。
import numpy as np
import matplotlib.pyplot as plt
# Keyオブジェクトの定義(識別子ベクトル)
class Key:
def __init__(self, vector):
self.vector = vector
# Valueオブジェクトの定義(取り出す情報ベクトル)
class Value:
def __init__(self, vector):
self.vector = vector
# Queryオブジェクトの定義(注目したい特徴ベクトル)
class Query:
def __init__(self, vector):
self.vector = vector
# Attention重みの計算(QueryとKeyの類似度)
def compute_attention_weights(self, keys):
scores = np.array([np.dot(self.vector, key.vector) for key in keys]) # 内積によるスコア
exp_scores = np.exp(scores - np.max(scores)) # softmaxのための安定化
attention_weights = exp_scores / np.sum(exp_scores) # softmax正規化
return attention_weights
# Attention重みを使ってValueを合成
def retrieve_values(self, keys, values):
attention_weights = self.compute_attention_weights(keys)
output = sum(w * v.vector for w, v in zip(attention_weights, values)) # 重み付き合成
return output, attention_weights
# サンプルのKeyとValueを作成
keys = [Key(np.array([1, 0, 0])), Key(np.array([0, 1, 0])), Key(np.array([0, 0, 1]))]
values = [Value(np.array([0.5, 0.2, 0.1])), Value(np.array([0.1, 0.7, 0.3])), Value(np.array([0.3, 0.4, 0.6]))]
# Queryを定義
query = Query(np.array([0.2, 0.8, 0.1]))
# 出力ベクトルとAttention重みを計算
output_vector, attention_weights = query.retrieve_values(keys, values)
# Attention重みの可視化
plt.figure(figsize=(6, 4))
plt.bar(range(len(attention_weights)), attention_weights, tick_label=[f"Key {i+1}" for i in range(len(keys))])
plt.title("Attention Weights (Query vs Keys)")
plt.xlabel("Keys")
plt.ylabel("Attention Weight")
plt.tight_layout()
plt.show()
# 出力ベクトルの表示
print("Output vector:", output_vector)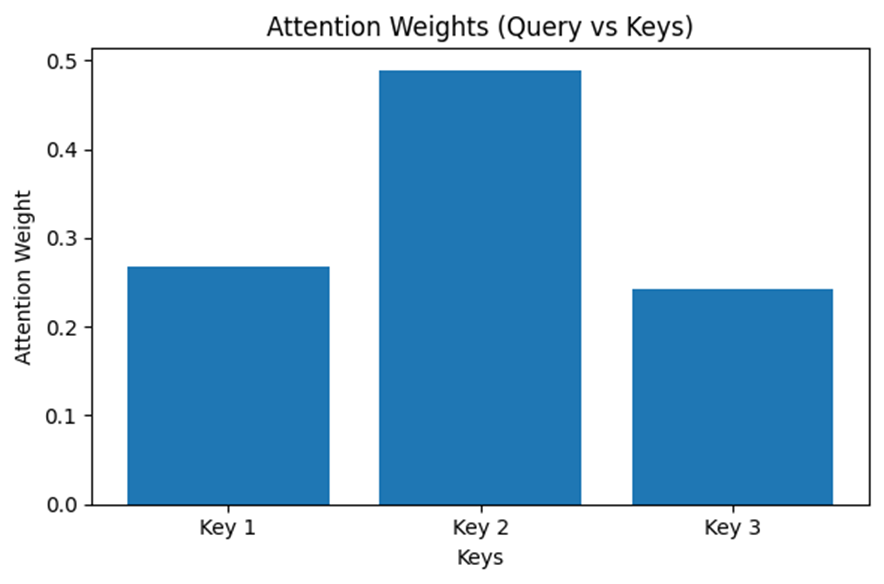
Output vector: [0.25588256 0.4930077 0.31917147]Self-Attentionと自己参照
オブジェクト指向における self と、Transformer系モデルにおける Self-Attention。これらは一見異なる領域に属する構造であるが、共に「自己を文脈の中で再評価・再構成する」という点で共通している。本節では、この「自己参照の構造」を線形代数的視点から接続し、両者に共通する抽象操作を明らかにする。
OOPにおける self:型文脈に依存する自己再評価
オブジェクト指向において self は、クラス内から自分自身のメソッドや属性にアクセスするための参照である。しかしそれは単なる静的な参照ではない。継承階層において self.do() と記述した場合、self の実体(=実行時型)に応じて適切な do() 実装が動的に選択される。
これは、self が「現在の型文脈において意味を持つ振る舞いの射影」として機能していることを意味する。self は、自身が属するクラスという文脈に応じて、定義済みの振る舞い(基底)から有効な成分を選択・再構成しているとも言える。これはまさに「基底空間の変換と射影」として理解可能である。
Self-Attentionにおける自己参照:意味文脈に依存する自己再構成
一方、Self-Attentionでは、系列中の各要素が自身を含む入力全体に対して注意(Attention)を行う。数式としては以下のように表される:
$$
\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\cdot V
$$
ここで $Q=XW^Q,K=XW^K,V=XW^V$ として、入力 $X$ を線形変換したベクトル間の類似度を計算し、重み付き和として自己ベクトルを“再構成”している。つまり、Self-Attentionは、全体文脈を通して「自己の重要性・意味」を再評価する構造であり、「注意重み」を通じて情報をフィルタリングし直す操作とみなせる。
この構造は、入力系列を張るベクトル空間における動的な射影演算としても解釈できる。Attentionは「どの軸が意味的に重要か」を学習的に選び取るため、自己ベクトルは常に「文脈によって定義され直された基底」によって表現される。
なお、Self-Attentionにおける Query(Q)、Key(K)、Value(V)は、単に同一の入力系列から取り出されるわけではなく、それぞれ異なる線形変換を通じて生成される。すなわち、以下のような構造が前提となる:
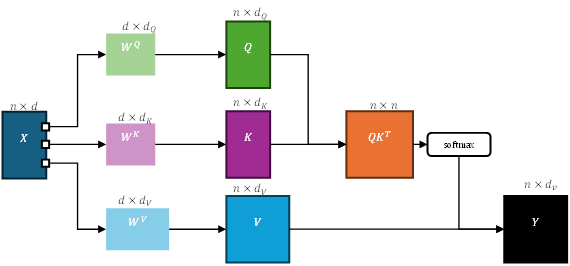
ここで $X$は入力系列、$W^Q,W^K,W^V$ はそれぞれの重み行列であり、Transformerにおける学習可能なパラメータである。この変換により、同一の入力ベクトルが「注目すべき特徴(Q)」「識別子(K)」「抽出対象(V)」という意味的に異なる空間へとマッピングされる。
この構造は、Attentionが単なる自己相似性の計算に留まらず、意味文脈に基づいた情報抽出機構として機能するための必須条件である。Q/K/Vの分離は、オブジェクト指向における「役割分担されたメソッド群の動的選択」にも通じるものであり、Self-Attentionの抽象性とOOPの構造的柔軟性との接点をより精緻に捉えるための重要な視点となる。
抽象構造としての共通点:文脈依存的自己評価
| 項目 | OOPの self | Self-Attention |
| 自己の定義 | クラス文脈に応じた振る舞い参照 | 入力系列文脈に応じた意味の再構成 |
| 動的性 | 実行時型に応じてメソッドが変わる | 各入力に応じて自己表現が変化 |
| 操作の構造 | 振る舞いの基底選択・再射影 | 意味的基底への重み付き射影 |
| 数学的解釈 | 基底変換 + 射影(型 ≒座標系の切り替え) | ソフトな基底再構成(軸のフィルタリング) |
| フィルタ的性質 | 実装継承を通じた有効な振る舞いの制限 | 重み付き注意により重要な軸を強調・抽出 |
統一的再解釈
両者の構造を線形代数の枠組みにおいて抽象化すれば、どちらも次のように捉えられる:
「自己成分を、ある文脈に基づいて再射影し、選択的に意味づけし直す操作」OOPにおける self は型空間における「射影的自己参照」、Self-Attention における self は意味空間における「動的フィルタ的自己参照」とも言える。
この対応は、オブジェクト指向とニューラルネットワークの形式構造が、いずれも「動的な基底選択と射影の枠組み」の中で記述可能であることを示唆している。両者は異なる次元で「自己を構成する空間的前提」を持っているが、その操作の核は共通している:自己は常に“他”との関係によって定義される。
例:シンプルなSelf-Attentionの実装
import numpy as np
import matplotlib.pyplot as plt
# トークン数と埋め込み次元の設定
num_tokens = 5
embedding_dim = 4
attention_dim = 4 # Attention空間の次元(通常はembedding_dimと同じか異なる)
# ランダムな埋め込みベクトルを生成(各トークンの特徴)
np.random.seed(42)
tokens = np.random.rand(num_tokens, embedding_dim)
# 重み行列の定義(線形変換:1×1 convに相当)
W_Q = np.random.rand(embedding_dim, attention_dim)
W_K = np.random.rand(embedding_dim, attention_dim)
W_V = np.random.rand(embedding_dim, attention_dim)
# Query, Key, Value の生成(線形変換)
Q = tokens @ W_Q
K = tokens @ W_K
V = tokens @ W_V
# Attentionスコアの計算(QとKの内積)
scores = Q @ K.T
# スケーリング(埋め込み次元の平方根で割る)
scaled_scores = scores / np.sqrt(attention_dim)
# softmaxによる正規化(各トークンが他トークンにどれだけ注目するか)
def softmax(x):
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True)) # 安定化
return exp_x / np.sum(exp_x, axis=-1, keepdims=True)
attention_weights = softmax(scaled_scores)
# 出力ベクトルの計算(ValueにAttention重みをかけて合成)
output_vectors = attention_weights @ V
# Attention重み行列の可視化
plt.figure(figsize=(6, 5))
plt.imshow(attention_weights, cmap='viridis')
plt.colorbar()
plt.title("Self-Attention Weight Matrix")
plt.xlabel("Attended Token Index")
plt.ylabel("Query Token Index")
plt.xticks(range(num_tokens))
plt.yticks(range(num_tokens))
plt.tight_layout()
plt.show()
# 出力ベクトルの表示(各トークンが自己参照を含めて合成した結果)
print("Output vectors (after self-attention):")
print(output_vectors)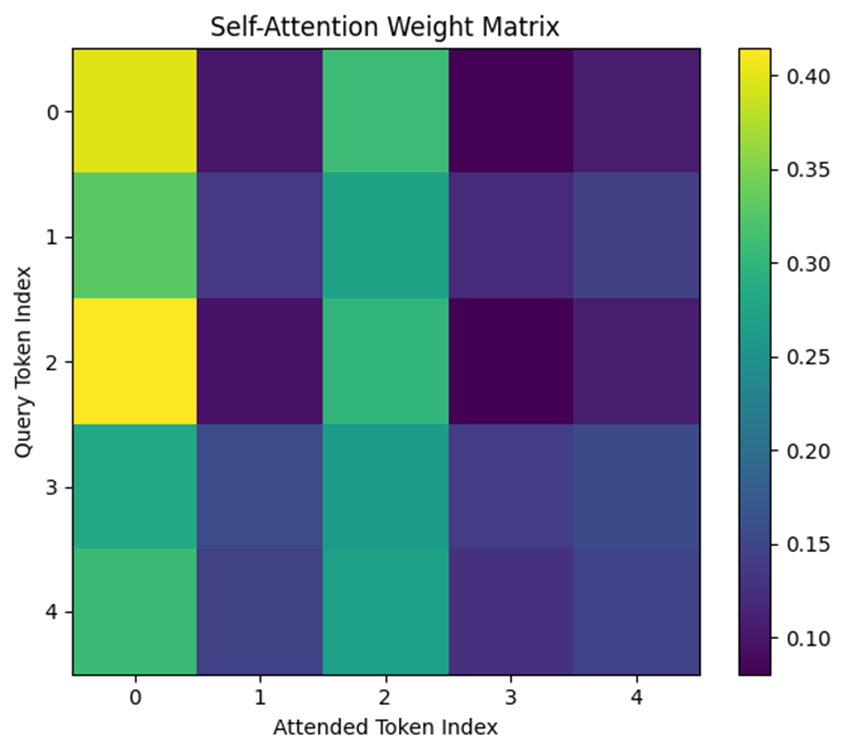
Output vectors (after self-attention):
[[0.8171592 1.00426184 0.69930635 1.31138005]
[0.7915625 0.96723906 0.66875262 1.25601252]
[0.81875423 1.00416968 0.70712603 1.31194758]
[0.77771824 0.94955796 0.64721517 1.2291082 ]
[0.7857578 0.9602772 0.65909118 1.24542999]]LLMの構造とオブジェクト指向の再解釈
LLMは、膨大なテキストデータを学習して、自然言語を理解・生成するAIモデル。GPTやBERTなどが代表例で、Transformerという構造を基盤としている。
大規模言語モデル(LLM)は、Transformerアーキテクチャを基盤としており、その中核にはSelf-Attention機構がある。これは、線形代数(行列演算)と非線形関数(softmaxなど)を繰り返し適用する構造であり、まさに「線形変換+非線形関数」の積み重ねである。
この構造をオブジェクト指向的に捉えると、各レイヤーは「状態を持ち、入力に応じて出力を返すオブジェクト」として機能している。Attention機構は、オブジェクト間の動的な関係性の構築、すなわち「どのオブジェクトがどのオブジェクトに注目するか」を計算するプロセスであり、これはポリモーフィズムや動的ディスパッチの高度な応用と見なすことができる。
さらに、LLMは自己教師あり学習によって、入力と出力の対応関係を大量のデータから学習する。このプロセスは、オブジェクトの「変換行列(重み)」をデータ駆動で最適化するものであり、オブジェクトの振る舞いを数理的に調整するという意味で、線形代数的な視点と完全に一致する。
このように、LLMの内部構造は、オブジェクト指向の抽象性と線形代数の演算性を融合したものであり、両者の接点を深く理解することで、AIモデルの設計原理に対する洞察が得られる。
以下の表は、オブジェクト指向を起点としつつ、Attentionや関数型プログラミングなどの抽象モデルを含めた設計構造の数理的対応関係を整理したものである。:
| 設計要素・抽象モデル | 線形代数的対応 | 圏論的対応 | 解説 |
| オブジェクト | 状態ベクトル + 変換行列 | 対象(Object) | 属性と振る舞いの統合 |
| 継承 | 行列の差分 | 射(構造変換) | 親 → 子の構造的写像 |
| ポリモーフィズム | 行列の切り替え | 射の選択 | 実行時に射を切り替える構造 |
| 条件分岐 | 非線形関数 | 射の分岐 | 入力に応じた射の選択(if → f(x)) |
| 関数合成 | 行列積 | 射の合成 | 処理の流れの抽象化 |
| Attention | 重み付き合成 | 射の加重合成 | 複数の射を重み付きで合成 |
| Self-Attention | 自己参照的合成 | 自己関手・自己射影 | 自分自身への射の構成 |
| 関数型プログラミング | 写像・関数合成 | 関手 | 型圏 → 実装圏の構造保存写像 |
本稿のモデルの適用範囲と限界
本稿では、オブジェクト指向の主要概念を線形代数とのアナロジーに基づいて再解釈し、現代の計算パラダイムとの構造的連続性を示してきた。このアナロジーは、ソフトウェア設計の根底にある数理構造を浮き彫りにする強力なレンズとなるが、万能ではない。議論の客観性と精緻さを担保するため、本モデルの適用範囲とその限界についても明確に言及しておく。
継承モデルの単純化
「継承を行列の差分($A_{child}=A_{parent}+\Delta A$)」と捉えるモデルは、振る舞いの拡張や修正を直感的に理解する上で極めて有効である。しかし、これはOOPが持つ複雑な継承セマンティクスを単純化した表現である。
- メソッドの完全なオーバーライド: 子クラスが親クラスのメソッドを全く利用せず、完全に新しい振る舞いを実装する場合、それは差分($\Delta A$)の追加というより、変換行列そのものの「置換」と捉える方がより実態に近い。
- インターフェースの実装: JavaやC#におけるインターフェースは、具体的な変換行列($A_{parent}$)を持たず、実装すべきメソッドの「型」や「シグネチャ」を定義する一種の構造的契約である。これは行列そのものというより、行列が満たすべき次元や入出力の型に関する制約と解釈すべきであり、本稿の単純なモデルでは直接的に表現しきれない。
- 多重継承の複雑性: 複数の親クラスから継承する場合、振る舞いの合成は単純な行列の加算では表現できない。メソッド名の衝突(ダイヤモンド問題など)を解決するためのルールは、線形代数の演算を超えた、プログラミング言語固有のロジックを必要とする。
「状態」表現の抽象化レベル
本稿では、オブジェクトの状態を「状態ベクトル」として抽象化した。これは物理シミュレーションやAIモデルの文脈では自然な表現だが、一般的なソフトウェアにおける状態はより多様である。
- 非ベクトル的な状態: 文字列、ファイルハンドル、あるいは他のオブジェクトへの参照といった状態は、本質的に数値ベクトルではない。これらをベクトル空間に写像(エンコーディング)する際には、何らかの設計上の判断や情報損失が伴う可能性がある。
- カプセル化と可視性: publicやprivateといったアクセス修飾子が定めるカプセル化の概念は、本モデルでは直接的に表現されていない。これは「変換行列のどの要素が外部から観測・操作可能か」という制約に対応するかもしれないが、より複雑な形式化を要する。
本章の意義
これらの限界点を認識することは、本稿のアナロジーの価値を何ら損なうものではない。むしろ、どの側面が数理モデルとして明快に対応し、どの側面がプログラミング言語の持つ歴史的・実践的な意味論(セマンティクス)に深く根差しているのかを明確に切り分けることにこそ意義がある。
本稿の提示する視点は、OOPの全てを網羅する厳密な数学理論ではなく、その数理的本質を照らし出し、AIや関数型プログラミングといった異分野との構造的類似性を探求するための、強力かつ生産的な思考ツールなのである。
結論:抽象化の先にある構造的真理
「オブジェクト指向を線形代数で捉える」という視点は、単なる思考実験ではなく、現代の計算モデルの本質に迫るための有効な抽象化手法である。AI、関数型プログラミング、並列処理といった分野との接続点を提供し、ソフトウェア設計の透明性と解析可能性を高める。
この視点を持つことで、以下のような利点が得られる:
- ソフトウェア設計における因果関係の明確化
- 条件分岐や状態遷移の数理的な記述
- 並列処理やバッチ処理の自然な導入
- AIモデルとの構造的な共通性の理解
エンジニアとしてこのような抽象的視点を持つことは、設計の精度と柔軟性を高め、数理的な裏付けを持ったソフトウェア構築を可能にする。
この抽象的視点の先には、ディープラーニングという現代の計算知能の核心が、確かに存在している。
そしてこの視点は、今後のAIシステム設計やソフトウェアアーキテクチャの抽象化にも応用可能であり、数理的な設計思考の重要性を再認識させるものである。
付録
線形代数的構造の補足
内積は方程式の別表現
ベクトルの内積は、一次関数や多項式の式を行列形式で表現する手段として捉えることができる。以下の2つの式は、見た目は異なるが、同じ意味を持っている。
一次関数の例:
$$
y = ax + b
$$
これは、次のようにベクトルの内積として表現できる:
$$
y=\begin{bmatrix} a & b \end{bmatrix} \begin{bmatrix} x \\ 1 \end{bmatrix}
$$
二次関数の例:
$$
y=ax^2+bx+c
$$
これも同様に、次のように書き換えられる:
$$
y = \begin{bmatrix} a & b & c \end{bmatrix} \begin{bmatrix} x^2 \\ x \\ 1 \end{bmatrix}
$$
このように、多項式の係数ベクトルと入力ベクトルの内積として関数を表現することで、数式の構造がより明確になる。
入力・変換・出力の分離による構造化
次のような2変数の連立一次方程式を考える:
\begin{cases}
x’ = ax + by \\
y’ = cx + dy
\end{cases}
この式は、入力・変換係数・出力の3つの要素に分解して、以下のように行列形式で表現できる:
$$
\begin{bmatrix}
x’ \\
y’
\end{bmatrix}=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
$$
さらに、出力から元の入力を求めたい場合は、逆行列を用いて次のように表現できる:
$$
\begin{bmatrix}
x \\
y
\end{bmatrix}=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}^{-1}
\begin{bmatrix}
x’ \\
y’
\end{bmatrix}
$$
これは、連立方程式を解く操作と数学的に同等である。
入出力の拡張とバッチ処理の構造
上記の変換を複数の入力に対して同時に適用する場合、列ベクトルの集合として扱うことで、行列演算によるバッチ処理が可能になる。
2組の入力・出力の場合:
$$
\begin{bmatrix}
x_1′ & x_2′ \\
y_1′ & y_2′
\end{bmatrix}=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
x_1 & x_2 \\
y_1 & y_2
\end{bmatrix}
$$
一般化してn組の入力・出力の場合:
$$
\begin{bmatrix}
x_1′ & x_2′ & \cdots & x_n’ \\
y_1′ & y_2′ & \cdots & y_n’
\end{bmatrix}=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
x_1 & x_2 & \cdots & x_n \\
y_1 & y_2 & \cdots & y_n
\end{bmatrix}
$$
このように、入力ベクトルを列方向に並べることで、複数のデータに対して一括で変換を適用でき、GPUなどによる並列処理にも自然に対応できる。
抽象構造理解のための圏論的補足
圏とは何か?(構造的直感の補足)
圏論は、数学における「構造とその変換」を抽象的に捉える理論である。圏とは、ざっくり言えば「もの(対象)と、それらをつなぐ変換(射)を集めた世界」のこと。たとえば、集合と写像、型と関数、空間と変換など、何かしらの“構造”と“構造を変える操作”があれば、それは圏としてみなすことができる。
圏の基本構成は以下の通り:
- 対象(object):構造そのもの。集合、型、空間など。
- 射(morphism):対象間の変換。関数、写像、構造保存操作など。
- 合成(composition):射を連続して適用する操作。関数合成や行列積に対応。
- 恒等射(identity):各対象に対して定義される「何もしない」変換。
このような構造は、集合論的な「ものの集まり」と、群論的な「変換の組み合わせ方」の両方を抽象化しており、関数型プログラミングやAIモデルの設計にも応用される。
さらに、圏と圏の間の対応関係を記述するのが関手(functor)である。関手は、ある圏の対象と射を、別の圏の対象と射に対応させる操作であり、変換の構造(合成や恒等性)を保ったまま写像する。これは、抽象的な構造を別の文脈に翻訳する装置として機能する。
「カテゴライズ」と圏論の違い(補足)
日常的に使われる「カテゴライズ(categorize)」という言葉は、一般には「分類する」「グループに分ける」といった意味で用いられる。これは、集合論的な視点に近く、対象の属性や条件に基づいて静的に整理する操作である。
一方、圏論における「カテゴリ(圏)」は、単なる分類ではなく、対象間の変換や構造の関係性そのものを記述する枠組みである。圏論は「分類」ではなく、「構造の写像と合成」を扱う。
つまり、「カテゴライズ」は構造の“中”での整理であり、圏論は構造の“間”をつなぐ視点である。
思考スタイルと数学的構造の対応(補足)
思考のスタイルもまた、数学的構造と対応させることでその性質が見えてくる:
- ロジカルシンキング
- 集合論的な「要素の関係性」に基づく思考。前提とルールに従って、順を追って結論を導く。
- クリティカルシンキング
- 群論的な「構造の整合性」を問う思考。前提や論理の妥当性を検証し、反例や矛盾を探る。
- ラテラルシンキング
- 圏論的な「構造間の写像と再構成」によって新たな視点を得る思考。枠組みそのものを変えて、異なる構造の間を横断する。
このように、圏論は「構造の中で考える」のではなく、「構造をまたいで考える」ための視点を提供する。本文で扱う抽象モデル(OOP、Attention、関数型など)を統一的に捉えるための補助線として、圏論的な理解は有効である。
参考文献・リンク
- 斎藤康毅 (2016). 『ゼロから作るDeep Learning―Pythonで学ぶディープラーニングの理論と実装』 , オライリー・ジャパン.
- Vaswani, A. et al. (2017). Attention is All You Need. [arXiv:1706.03762] https://arxiv.org/abs/1706.03762
- Jay Alammar(2018). The Illustrated Transformer. https://jalammar.github.io/illustrated-transformer/
- 斎藤康毅 (2018). 『ゼロから作るDeep Learning ②―自然言語処理編』, オライリー・ジャパン.
その他のエッセイはこちら
予備校のノリで学ぶ線形代数~単位も安心 速習テスト対策5講義付き! (ヨビノリ)
ゼロから学ぶ線形代数
ゼロから作るDeep Learning―Pythonで学ぶディープラーニングの理論と実装
ゼロから作るDeep Learning ②―自然言語処理編




コメント