データの性質や導線設計の話は断定ですか？

断定ではなく推測です。係数設定の足場として提示し、結論は用途（w）で期待値が逆転しうる構造の説明に限定しています。特に導線設計仮説は、事実（公式に言える範囲）→推測（飛躍点の明示）→検証可能な予測の順に分け、推測が独り歩きしないようにしています。

ChatGPTとGeminiの違いは「性能差」より“検索・根拠・提案”の初期設定：体感 → 仮説 → パラメータ分解 → おもちゃモデル

Q: この記事の「体感」は事実ですか？

事実ではありません。個人の感想・推測として明示し、その推測を係数に写像した玩具モデルの前提条件として扱っています。

Q: 事実として言えることは何ですか？

検索や引用（根拠提示）に関する機能が存在することは各社ドキュメントに記載があります（末尾の参考文献URL）。

その他の数理的なエッセイはこちら

はじめに（前提の明示）
体感（個人の推測）：ChatGPTはこう、Geminiはこう
1. Geminiに寄って見えやすい体感（推測）
2. ChatGPTに寄って見えやすい体感（推測）
“そう見える”かもしれない理由（これも個人の推測）
1. 持っているデータ／アクセスできる情報の性質が違う可能性（推測）
2. “次の一手”を価値に置く設計が提案を増やす可能性（推測）
体感をパラメータに分解する（係数の設計図）
期待値としての「体感性能」
1. 余談：離散と連続での見え方（イメージ用）
ミニシナリオ（用途を $w$ に落とす）
1. 会議前の市場調査（ざっくり調査寄り）
2. 仕様・規格・稟議の根拠確認（根拠必須寄り）
おもちゃモデル（数式：シンプルに）
係数表（仮置き：体感を写像しただけ）
1. システム側係数（ChatGPT-like / Gemini-like）
2. 共通係数（モデル形状・ペナルティの強さ）
Pythonコード（シミュレーション＆グラフ）
感度チェック（逆転点はどれくらい動く？）
読み取り方（“どっちが上”ではなく“どこで逆転するか”）
まとめ
FAQ
参考文献（URL明記）
体感と思考の罠を壊す（バイアス／ノイズ／選択設計）
期待値・不確実性・予測（「どっちが上」より“どこで逆転するか”の素地）
検索・根拠・評価（Grounding／引用／“g”を支える土台）
「ベンチマークを取らない」ではなく「評価の型を持つ」（指標・評価・測定の勘所）
“初期設定”は実装と運用で決まる（MLOps／LLMOps／プロダクト設計）

はじめに（前提の明示）

この記事に出てくる「ChatGPTはこう感じる」「Geminiはこう感じる」は、完全に個人の感想・推測です。ベンチマーク結果でも、検証済みの事実でもありません。

この“体感（推測）”は、後半のおもちゃモデルで係数を仮置きするための前提として使います。
一方で、「検索や引用（根拠提示）に関する機能が存在する」こと自体は各社ドキュメントに記載があります（参考文献としてURLを末尾に明記します）。

Gemini API：Google検索でグラウンディングして引用（citations）を付ける説明
URL：https://ai.google.dev/gemini-api/docs/google-search
ChatGPT：ChatGPT search の紹介（プロダクトとしての検索の位置づけ）
URL：https://openai.com/index/introducing-chatgpt-search/
ChatGPT（Enterprise/Edu）：利用上の整理（機能としての検索の扱い）
URL：https://help.openai.com/ja-jp/articles/10093903-chatgpt-search-for-enterprise-and-edu

本稿で言う「初期設定」は、モデル単体の能力差というより、検索・引用・提案など“回答の出し方”を規定するデフォルト挙動（UI/ツール/ワークフロー設計）が体感に与える影響、という意味で扱います。
プロダクト（Web/モバイル、Enterprise、API）や設定で挙動は変わりうるため、以下の係数は「一意に正しい」ものではなく、逆転しうる構造を説明するための足場です。

体感（個人の推測）：ChatGPTはこう、Geminiはこう

差が出やすいと感じる点を、あえて明確に書きます（繰り返し：推測です）。

Geminiに寄って見えやすい体感（推測）

ざっくり調査（全体像・比較軸・候補・次アクション）で「前に進む」回答になりやすい
厳密さより「暫定解をまず出す」方向に見えやすい
“提案”が厚いほど、体感として「気が利く」「優秀」に見えやすい

ChatGPTに寄って見えやすい体感（推測）

根拠が必要な調査（一次情報・引用・前提の切り分け）で安心に見えやすい
断定を抑え、不確実性や前提条件を分けて書く方向に見えやすい
引用（ソース）を踏んでレビューする導線があると、確認作業につなげやすい

“そう見える”かもしれない理由（これも個人の推測）

ここからは背景仮説です。狙いは「断定」ではなく、後半で係数を置くための足場を作ることです。

持っているデータ／アクセスできる情報の性質が違う可能性（推測）

Google側は検索を含む巨大な情報基盤を持つため、「概略（＝二次情報的なまとめ）を厚くして前に進める」設計が合理的になりやすい、という仮説です。少なくとも、Gemini APIにはGoogle検索でグラウンディングして引用を付ける使い方が記載されています。
URL：https://ai.google.dev/gemini-api/docs/google-search

この仮説をおもちゃモデルへ写像するなら、Gemini側は 概略寄りの係数や 提案の厚みの係数を高めに置く、という扱いになります。

“次の一手”を価値に置く設計が提案を増やす可能性（推測）

検索プロダクトは構造的に「探索→次アクション」の導線を価値として扱いやすい、という仮説です。AI Overviews周辺の広告についての説明は公開されています。
URL：https://support.google.com/google-ads/answer/16297775?hl=en

事実（言える範囲）：公式説明からは、AI Overviewsに広告が表示されうること、また“次の一手”を促す導線が価値として扱われていることが読み取れます。
URL：https://support.google.com/google-ads/answer/16297775?hl=en
推測（ここから先）：この導線設計（広告目的と断定しない）が、生成回答のスタイルにも（少なくとも一部で）影響し、結果として「候補」「比較軸」「次に調べる観点」などの 提案が厚めに見える可能性があります。
注意（断定しない）：提案の厚みは、UIテンプレ・ツールの既定ワークフロー・安全性設計など、別要因でも説明し得ます。
検証可能な予測：もしこの仮説が効いているなら、同一プロンプト集合で（a）次アクション提案の数、（b）「次に検索するなら…」型の頻度、（c）外部参照の導線の出方、などに差として現れやすいはずです（逆なら棄却しやすい）。

これをおもちゃモデルへ写像するなら、Gemini側は 提案の効用（gain）が体感に寄与しやすい、として表現できます。

体感をパラメータに分解する（係数の設計図）

体感（推測）を、次の変数に落とします。

根拠（一次情報・引用）寄りの強さ：$g$
概略（二次情報込み）寄りの強さ：$c$
提案の厚み（次アクションをどれだけ出すか）：$p$
ユーザー側の根拠重視度（用途の違い）：$w \in [0,1]$
- $w$ が小さい：ざっくり調査寄り
- $w$ が大きい：根拠必須寄り

さらに「平均の取り方」を表すために、質問分布 $\mathcal{D}$ を置きます（普段どんな質問が多いか、という偏り）。

期待値としての「体感性能」

体感性能を、次の1行に固定します。

$$
Q = \mathbb{E}_{q \sim \mathcal{D}}[U(R(q), q)]
$$

$q$：質問（クエリ）
$\mathcal{D}$：普段投げる質問の偏り（分布）
$R(q)$：AIの応答
$U$：満足度（根拠・概略・提案・リスクの合成）

この式が言っていることは、「どっちが優秀？」は 平均の取り方（$\mathcal{D}$ と $U$）次第で変わる、という点です。

余談：離散と連続での見え方（イメージ用）

離散（質問タイプが数えられる）
$$
Q = \sum_i P(q_i) \cdot U(R(q_i), q_i)
$$

連続（難易度など連続量で扱う）
$$
Q = \int U(R(q), q) \cdot p(q) dq
$$

ミニシナリオ（用途を $w$ に落とす）

会議前の市場調査（ざっくり調査寄り）

欲しい：全体像、比較軸、候補、次の一手
成功条件：60～80点でよいので前に進む
モデル上の解釈：$w$ が小さめ（概略と提案の寄与が効く）

仕様・規格・稟議の根拠確認（根拠必須寄り）

欲しい：一次情報、引用、断定の根拠、前提条件
成功条件：誤りが高コスト
モデル上の解釈：$w$ が大きめ（根拠と誤りペナルティが効く）

おもちゃモデル（数式：シンプルに）

現実の再現ではなく、「用途で逆転しうる構造」を描くための玩具です。

難易度（質問のしんどさ）を正規分布で振ります。

$$
d \sim \mathcal{N}(0,1)
$$

ロジスティック関数：

$$
\sigma_k(x)=\frac{1}{1+e^{-kx}}
$$

根拠側品質／概略側品質（傾斜違いロジスティック）：

$$
q_{\mathrm{pri}}=\sigma_{k_1}(g-d),\quad
q_{\mathrm{sec}}=\sigma_{k_2}(c-d)
$$

用途の違い $w$ による混合（線形）：

$$
q_{\mathrm{mix}} = w q_{\mathrm{pri}} + (1-w) q_{\mathrm{sec}}
$$

誤りリスクと指数ペナルティ（外すコストの表現）：

$$
r=\sigma_{k_3}(d-g),\quad
\mathrm{pen}=\lambda(e^{\alpha r}-1)
$$

提案の効用（探索寄りで効く：$w$ が小さいほど乗る）：

$$
\mathrm{gain}=\mu(1-w)\log(1+p)
$$

最終効用と期待値：

$$
U=q_{\mathrm{mix}}+\mathrm{gain}-\mathrm{pen},\quad
Q=\mathbb{E}[U]
$$

係数表（仮置き：体感を写像しただけ）

この表は「現実」ではなく、前半の体感（推測）を再現するための仮置きです。係数を少し動かすだけで結果は簡単に変わります。

システム側係数（ChatGPT-like / Gemini-like）

パラメータ	意味	ChatGPT-like（仮）	Gemini-like（仮）
$g$	根拠（一次情報・引用）寄りの強さ	1.1	0.7
$c$	概略（二次情報込み）寄りの強さ	0.4	1.0
$p$	提案の厚み	0.6	1.2

共通係数（モデル形状・ペナルティの強さ）

パラメータ	意味	値（仮）
$k_1$	根拠側ロジスティックの傾斜	2.0
$k_2$	概略側ロジスティックの傾斜	1.2
$k_3$	リスク側ロジスティックの傾斜	1.5
$\lambda$	ペナルティ係数	0.7
$\alpha$	指数ペナルティの鋭さ	1.6
$\mu$	提案効用の係数	0.25

Pythonコード（シミュレーション＆グラフ）

import numpy as np
import matplotlib.pyplot as plt

def sig(x, k=1.0):
    return 1 / (1 + np.exp(-k * x))

def expected_utility(params, w, N=20000, seed=0):
    rng = np.random.default_rng(seed)
    d = rng.normal(0, 1, N)  # difficulty ~ Normal(0, 1)

    g, c, p = params["g"], params["c"], params["p"]

    # qualities
    q_pri = sig(g - d, k=2.0)   # k1
    q_sec = sig(c - d, k=1.2)   # k2
    q_mix = w * q_pri + (1 - w) * q_sec

    # risk -> exponential penalty
    risk = sig(d - g, k=1.5)    # k3
    pen  = 0.7 * (np.exp(1.6 * risk) - 1)  # lambda, alpha

    # proposal gain: stronger for exploration-like usage (low w)
    gain = 0.25 * (1 - w) * np.log1p(p)    # mu

    U = q_mix + gain - pen
    return U.mean()

# toy coefficients (see table)
chatgpt_like = {"g": 1.1, "c": 0.4, "p": 0.6}
gemini_like  = {"g": 0.7, "c": 1.0, "p": 1.2}

ws = np.linspace(0, 1, 41)  # w: evidence importance
Qc = np.array([expected_utility(chatgpt_like, w, seed=1) for w in ws])
Qg = np.array([expected_utility(gemini_like,  w, seed=1) for w in ws])
diff = Qg - Qc

plt.figure()
plt.plot(ws, Qc, label="ChatGPT-like")
plt.plot(ws, Qg, label="Gemini-like")
plt.xlabel("w (evidence importance)")
plt.ylabel("Expected utility Q")
plt.title("Toy model: relative advantage can flip depending on w")
plt.legend()
plt.show()

plt.figure()
plt.plot(ws, diff)
plt.axhline(0)
plt.xlabel("w (evidence importance)")
plt.ylabel("Gemini-like - ChatGPT-like")
plt.title("Positive values favor Gemini-like")
plt.show()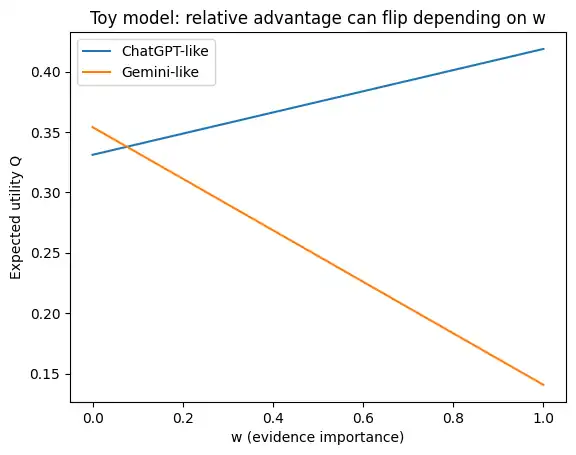

根拠重視度 w を横軸、期待効用 Q を縦軸に取り、ChatGPT-like と Gemini-like の2本の線を比較したグラフ。 — おもちゃモデル：根拠重視度 w によって期待効用 Q がどう変わるか（ChatGPT-like vs Gemini-like）

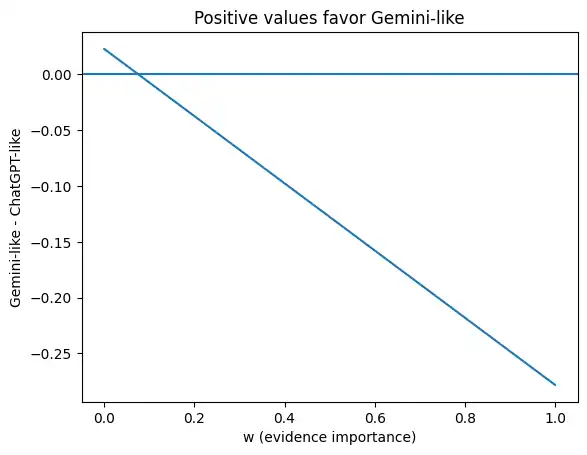
根拠重視度 w を横軸、期待効用 Q を縦軸に取り、ChatGPT-like と Gemini-like の2本の線を差のグラフ。 — おもちゃモデル：根拠重視度 w によって期待効用 Q の差がどう変わるか

感度チェック（逆転点はどれくらい動く？）

上の係数（表の値）で「どちらが有利か」が切り替わる点を $w^*$（= $Q_{\mathrm{Gemini}}-Q_{\mathrm{ChatGPT}}=0$ となる根拠重視度）とすると、基準設定では $w^*$ は小さめ（0.1未満）に出やすい、というのが直感に合う見え方になります。
ただし、係数を ±20% 動かすだけで $w^*$ は大きく動きます（そして場合によっては“逆転が消える”こともあります）。

たとえば同じコード設定（乱数シード固定）でも、以下のように変わります（“None”は「全域で逆転しない」＝一方が常に不利）。

ChatGPT-like の $g$ を -20%：逆転点が大きく右へ移動（根拠寄り優位が弱まる）
Gemini-like の $g$ を +20%：逆転点が右へ移動（根拠寄りが強くなる）
$p$ を動かす：逆転点は動くが $g$ ほど支配的ではないケースが多い
Gemini-like の $p$ を -20%：逆転なし（全域でChatGPT-like優位）になるケースが出る

この感度チェックが言いたいのは、「逆転点の数値そのもの」より、どの係数が逆転点を支配しやすいか（この例では $g$ の影響が特に大きい）を見せることです。

読み取り方（“どっちが上”ではなく“どこで逆転するか”）

$w$ が小さい（ざっくり調査寄り）ほど、$c$ と $p$ の寄与が効きやすい（gain も $(1-w)$ で乗りやすい）
$w$ が大きい（根拠必須寄り）ほど、$g$ とペナルティが効きやすい

この玩具の狙いは、「特定の係数を置けば必ずこうなる」ではなく、用途（$w$）で期待値が逆転しうるという構造を見せることです。

まとめ

本稿の主張は「ChatGPTが上／Geminiが上」ではなく、“体感差”を生む要因を（推測として）分解し、用途で優位が入れ替わり得る構造を示すことにあります。

体感（推測）を 根拠 $g$ / 概略 $c$ / 提案 $p$ と、用途側の重み $w$ に落とすと、「どっちが優秀か」は平均の取り方（$\mathcal{D}$ と $U$）で変わる、と表現できます。
“そう見える理由”として、検索・グラウンディングなどの情報アクセス特性に加え、検索プロダクトにおける“次の一手”設計が提案の厚みに寄与する可能性を置きました。ただしここは 事実→推測を分離し、推測が独り歩きしないようにしています（AI Overviews の広告表示に関する公式説明）。
URL：https://support.google.com/google-ads/answer/16297775?hl=en
おもちゃモデルは現実再現ではなく、$w$（用途）によって期待値が逆転しうることを可視化するためのものです（逆転点は係数に敏感で、±20%でも大きく動きます）。

まとめのまとめ

比較は「性能」ではなく 期待値（用途×効用）で決まる
体感差は 根拠/概略/提案のデフォルトで説明できるかもしれない
重要なのは「どっちが上」より どこで逆転するか

FAQ

この「体感」は事実ですか？

事実ではありません。個人の感想・推測として明示し、その推測を係数に写像した“玩具モデル”の前提条件として扱っています。

事実として言えることは何ですか？

検索や引用（根拠提示）に関する機能が存在すること自体は、各社ドキュメントに記載があります（末尾の参考文献URL）。
Gemini（Google検索でのグラウンディング）：https://ai.google.dev/gemini-api/docs/google-search
ChatGPT search（紹介ページ）：https://openai.com/index/introducing-chatgpt-search/
ChatGPT search（Enterprise/Edu）：https://help.openai.com/ja-jp/articles/10093903-chatgpt-search-for-enterprise-and-edu

「データの性質」や「導線設計」仮説は言い過ぎになりませんか？

断定しないために「推測」と明記しています。本文でも“背景仮説”として、係数設定の足場に留めています。特に導線設計については、本文中で 事実（公式に言える範囲）→推測（飛躍点の明示）→検証可能な予測 の順に分け、推測が独り歩きしないようにしています（AI Overviews と広告に関する公式説明）。
URL：https://support.google.com/google-ads/answer/16297775?hl=en