バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエの積分公式を求める話の続き。
前回は、角周波数ωの刻みであるΔωが0に近付くときの極限とし、離散から連続に考え方を変えるアプローチをとった。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】Δωが0に近付くときの極限とした式

まずは、前回の極限の式を再掲。
\(
\displaystyle f(x)=\lim_{\begin{eqnarray}\Delta\omega\to 0\\L\to\infty\end{eqnarray}}
\sum_{n=-\infty}^\infty \bigg\{ \frac{1}{2\pi}\int_{-L}^L f(t)e^{-i\omega_n t}\,dt \bigg\}e^{i\omega_n x}\Delta\omega
\)

何度見てもヤベェ式だな・・・。
区分求積法とリーマン積分

ここで区分求積法を用いる。

区分求積法?

積分を求める際の最もシンプルな近似法だな。
図にするとこんなイメージになる。
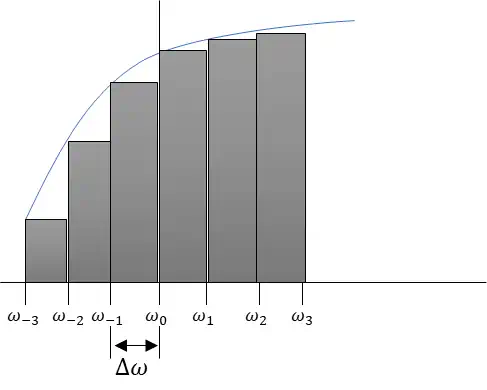

あー、高校数学の積分の話の時に見た気がする。
リーマン積分ってやつだっけ?

区分求積法とリーマン積分はとても似ているが、じつはちょっと違う。
区分求積法の\(\Delta x\)が0に近付くときの極限とした場合にリーマン積分になる。
って感じだな。

ここでポイントとなるのは、
区分求積法の段階では離散的だが、りーま積分にすると連続的になるってところ。
式で表現すると以下が成立するという話になる。
\(
\displaystyle\lim_{\Delta x\to0}\sum_{n=-\infty}^{\infty}G(x_n)\Delta x=\int_{-\infty}^{\infty}G(x)\,dx
\)
離散から連続へ

とすると、さっきの極限を用いた式の\(\displaystyle\sum\)が\(\displaystyle\int\)になるってことか。

正解。

式にすると以下になる。
\(
\displaystyle f(x)=\int_{-\infty}^{\infty}\bigg\{ \frac{1}{2\pi}\int_{-\infty}^{\infty}f(t)e^{-i\omega t}\,dt \bigg\}e^{i\omega t}\,d\omega
\)

これが「フーリエの積分公式」と呼ばれるものだ。
あとになるとわかることだが、逆フーリエ変換と同じ式ともいえる。
この式を示しているのは、以下の式が、
複素指数関数との積を2回行っても成立するというところだな。
\(
f(x)=f(t)
\)

演算したはずなのに変化しないってことか。
確かに不思議な現象だ。

まぁ、これが変換と逆変換ができることの証明とも言えるわけだ。
まとめ

まとめだよ。
- 区分求積法とリーマン積分について。
- 離散と連続の分け目。
- フーリエの積分公式を導出した。
- 演算したはずなのに変化しない。
- つまり変換、逆変換が成立することを示している。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント