探索と行動選択
本節では、エージェントが「どのように行動を選ぶか」を扱う。鍵となるのは 探索と活用(exploration-exploitation)のトレードオフ である。すなわち、既知の最善を用いて確実な報酬を得るか(活用)、未知の行動を試してより良い選択肢を発見するか(探索)を、状況に応じて両立させる設計である。
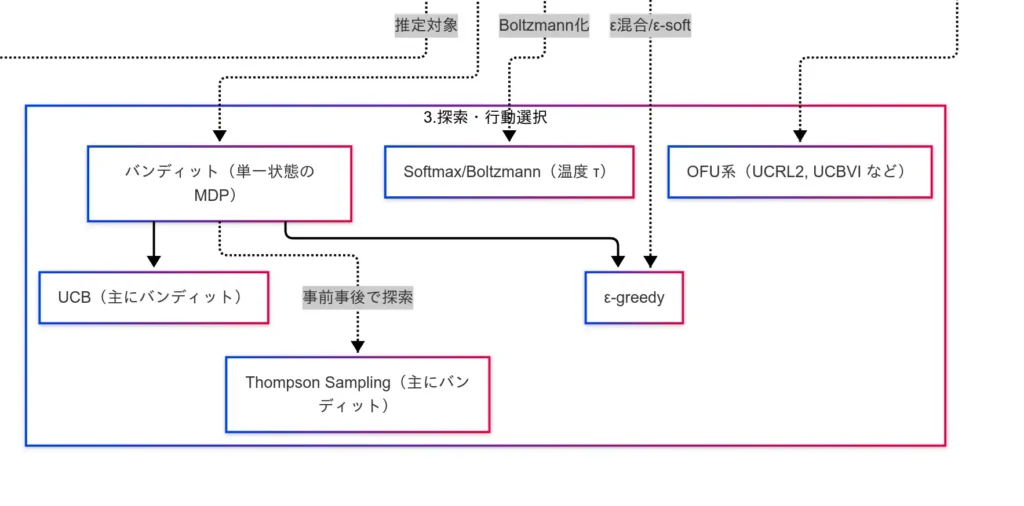
バンディット問題(単一状態の MDP)
状態が一つだけの MDP を想定し、複数の腕(行動)のうちどれを引くかを学ぶ簡約モデルである。探索戦略の多くはまずバンディットで導入され、MDP へ拡張される。
ε-greedy(ε‐貪欲)
既知の最善行動を確率 $1-\epsilon$ で選び、確率 $\epsilon$ で一様ランダムに探索する単純かつ強力な基準である。
$$
\pi(a|s) = \begin{cases}
\displaystyle 1-\epsilon+\frac{\epsilon}{|A|}\ \ &\ &\text{if}\ a=\arg\max_{a^\prime}Q(s,a^\prime)\\
\displaystyle\frac{\epsilon}{|A|}\ &\ &\text{otherwise}
\end{cases}
$$
$\epsilon$ の スケジューリング(例:線形減少、指数減衰) により、学習初期は探索を厚く、終盤は活用を重くする設計が一般的である。
Softmax / Boltzmann 方策
行動価値を確率に変換して抽選する方法である。温度 $\tau>0$ によりランダム度を調整する。
$$
\pi(a|s) =\frac{\exp(Q(s,a)/\tau)}{\sum_{a^\prime}\exp(Q(s,a^\prime)/\tau)}
$$
- $\tau\downarrow0$ で貪欲化、$\tau\uparrow0$ でほぼ一葉選択となる。
- 値の差に滑らかに反応するため、ε-greedy よりも微妙な差を反映しやすい。
UCB(Upper Confidence Bound)
推定値に 不確実性(信頼上限) を加点して選ぶ戦略である。典型例として UCB1 は腕 $a$ を
$$
\underbrace{\hat{\mu}_a}_{\text{経験平均}} + \underbrace{c \sqrt{\frac{\ln t}{n_a}} }_{\text{不確実性(探索ボーナス)}}
$$
でスコアリングし、最大の腕を選ぶ。ここで $t$ は総試行数、$n_a$ は腕 $a$ の試行回数である。
- 試行回数が少ない腕は不確実性が大きく、理にかなった探索 が自動で促進される。
Thompson Sampling
腕の報酬分布に事前分布を置き、観測により事後を更新しつつ、事後からサンプリングしたパラメータで最善腕を選ぶ ベイズ的戦略である。
- 不確実性の扱いが自然で、実装も簡潔であり、経験的性能が高いことが多い。
OFU 系(Optimism in the Face of Uncertainty)
不確実な部分を 楽観的に評価 して方策を選ぶ立場である。MDP 全体に拡張した代表例に UCRL2、UCBVI などがある。
- 遷移確率や報酬の推定区間の「上側」を用いて最適化することで、探索を理論的に保証する枠組みである。
受験上の要点
- バンディット=単一状態の MDP という位置づけを押さえること。
- ε-greedy は簡便で強力、Softmax は温度で滑らかに制御、UCB/Thompson は不確実性を明示的に扱う。
- OFU は MDP 全体での探索保証の文脈で登場(UCRL2/UCBVI の名称を把握しておく)。
以上で探索と行動選択の基礎が整った。次節では、これらの上に立つ 代表的アルゴリズム(Q 学習、SARSA、方策勾配、Actor-Critic)を確認する。
代表的アルゴリズム
本節では、強化学習の実装で頻出となる代表的手法を概観する。土台は TD 学習であり、その上に SARSA/Q 学習(価値ベース)、REINFORCE(方策ベース)、そして両者を統合する Actor-Critic が位置づく構図である。
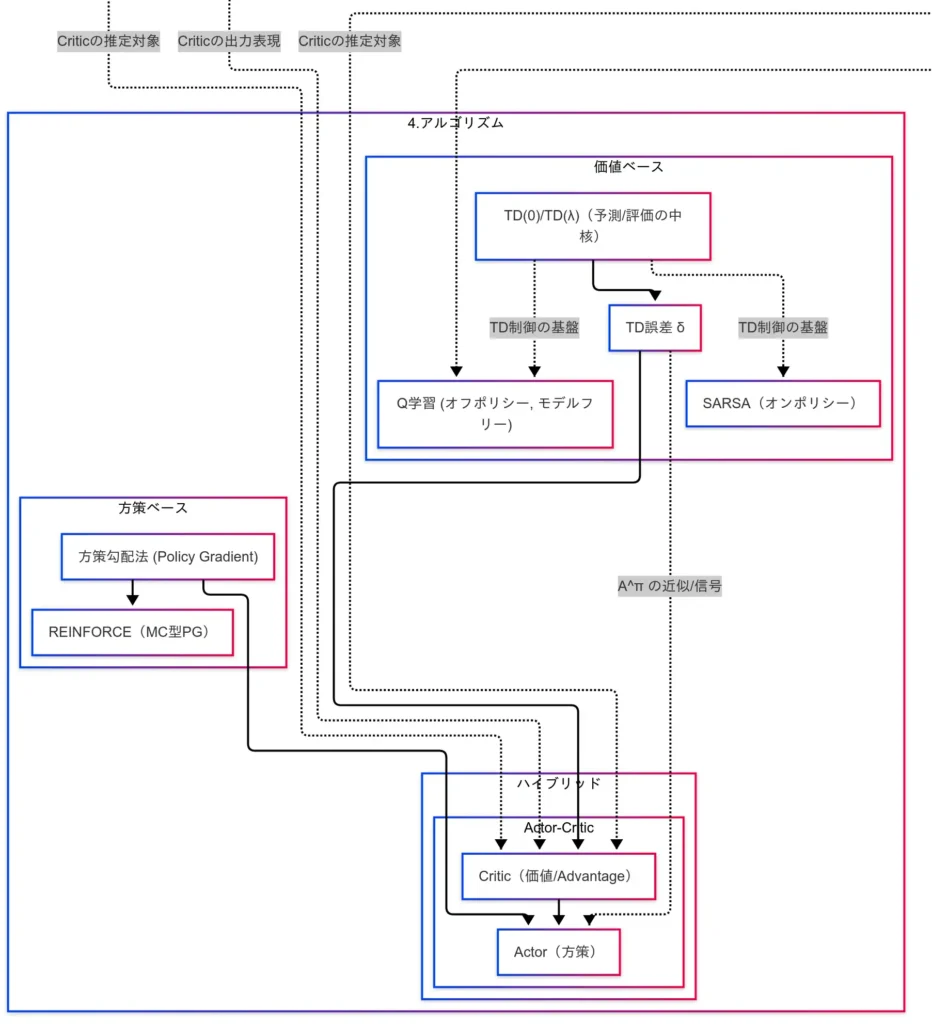
TD 学習(Temporal Difference)
将来の最終結果を待たず、途中推定で更新できる逐次学習である。更新式は次のとおりである。
$$
V(s)\leftarrow V(s)+\alpha[R_{t+1}+\gamma V(s^\prime)-V(s)]
$$
角括弧内は TD 誤差 $\delta$ であり、「予測と実測のズレ」を表す信号である。以降の多くの手法で、この $\delta$ が更新の芯として機能する。
SARSA(オンポリシー)
実際に選んだ次行動 $\alpha^\prime$ を用いて更新する、方策一貫性重視の制御である。
$$
Q(s,a)\leftarrow Q(s,a)+\alpha[R_{t+1}+\gamma Q(s^\prime,a^\prime)-Q(s,a)]
$$
オンポリシー であるため、学習中の方策に忠実で安全側に働きやすい一方、収束速度は遅くなる場合がある。
Q 学習(オフポリシー)
次状態での 最良行動価値 を仮定して更新する、オフポリシー制御である。
$$
Q(s,a)\leftarrow Q(s,a)+\alpha[R_{t+1}+\gamma \max_{\alpha^\prime}Q(s^\prime,a^\prime)-Q(s,a)]
$$
理論的には最適方策へ収束しやすいが、探索が不足すると推定が偏る危険がある。探索戦略(ε-greedy 等)との併用設計が実務上の肝である。
方策勾配法:REINFORCE(モンテカルロ型)
価値を介さず 方策そのもの のパラメータ $\theta$ を最適化する手法である。
$$
\theta\leftarrow\theta+\alpha G_t \nabla_\theta\log \pi_\theta(a|s)
$$
ここで $G_t$ は時刻 $t$ 以降の累積報酬である。エピソード完了後に更新する モンテカルロ型 であり、分散が大きくなりやすいため、実務ではベースライン(例:$V(s)$)減算による分散低減が併用されることが多い。
Actor-Critic(ハイブリッド)
Actor が方策を、Critic が価値(またはアドバンテージ)を担当する統合手法である。Critic が算出する TD 誤差 $\delta$ を学習信号として Actor を更新する。
$$
\begin{align}
\text{Critic}&: V(s)\leftarrow V(s)+\alpha\delta\\
\text{Actor}&: \theta\leftarrow\theta+\beta\delta\nabla_\theta\log\pi_\theta(a|s)
\end{align}
$$
オンライン更新が可能で、方策勾配の表現力と TD の効率性を兼ね備える点が利点である。直感的には Actor=プレイヤー/Critic=解説者 という役割分担で捉えると良い。
受験上の要点
- SARSA=オンポリシー、Q 学習=オフポリシー を取り違えないこと。
- TD 誤差 $\delta$ が多手法に共通する更新信号である点を把握すること。
- REINFORCE はモンテカルロ型で分散が大きくなりやすい(ベースラインで低減)こと。
- Actor-Critic は価値推定と方策更新のハイブリッドであり、実用性が高いこと。
以上で代表的アルゴリズムの骨格が揃う。次節では、これまでの要点を因果関係図に沿って総括する。
まとめ
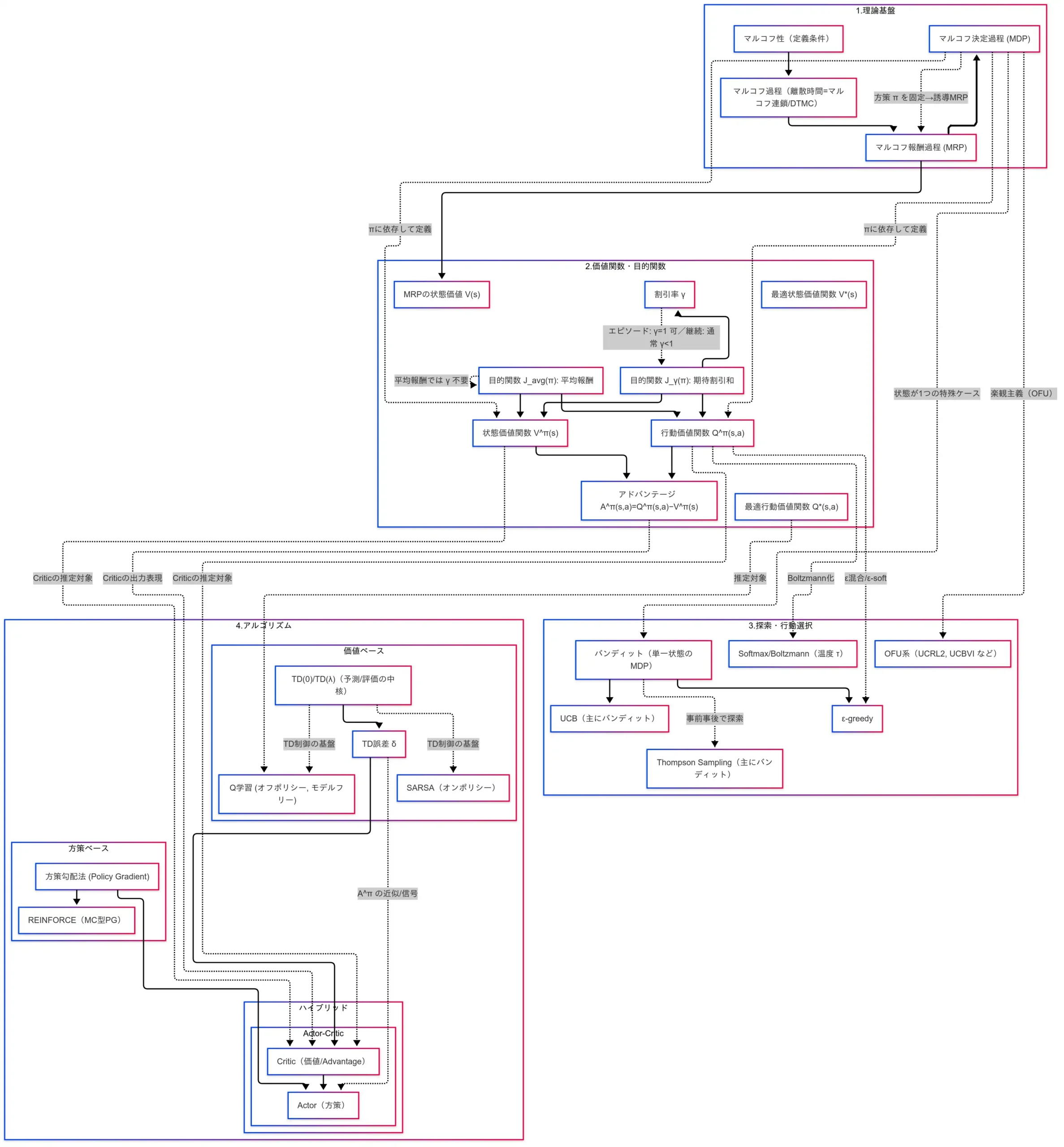
本稿では、因果関係図に沿って強化学習の土台を俯瞰した。まず 理論基盤 として、 マルコフ性 → マルコフ過程(DTMC) → MRP → MDP → 誘導MRP の階段を確認した。MDP が中心モデルであり、方策 $\pi$ を固定すれば MRP に還元されるという対応関係が要点である。すなわち「性質 → 過程 → 報酬 → 行動」という拡張の流れを押さえることが、後続の理解を支える。
次に 価値関数・目的関数 として、$V^\pi(s)$(状態のみ)、$Q^\pi(s,a)$(行動込み)、$A^\pi(s,a)=Q^\pi-V^\pi$(差分)の役割分担を整理し、最適版 $V^,Q^$ の位置づけを確認した。目的関数は 期待割引和 $J_\gamma$ と 平均報酬 $J_{\text{avg}}$ の二系統であり、割引率 $\gamma$ は「未来をどれだけ重視するか」のノブである。
探索と行動選択では、バンディット(単一状態の MDP)を土台に、ε-greedy(単純・堅実)、Softmax/Boltzmann(温度で滑らか制御)、UCB(信頼上限で理性的探索)、Thompson Sampling(ベイズ的探索)、OFU 系(UCRL2/UCBVI)を概観した。いずれも 探索‐活用トレードオフ をどう設計するかが核である。
最後に 代表的アルゴリズム として、TD 学習(逐次更新・TD 誤差 $\delta$)、SARSA(オンポリシー)、Q 学習(オフポリシー)、REINFORCE(方策勾配・MC 型)、Actor-Critic(価値推定×方策更新のハイブリッド)を整理した。直感的には Actor=プレイヤー/Critic=解説者 と捉えると運用イメージが掴みやすい。
以上の対応関係を図で往復できれば、用語の断片が線で結び直され、問題文の意図も読み取りやすくなるはずである。次の学習ステップとして、DQN、A2C/A3C、TRPO、PPO、分布型 DQN(Categorical/Rainbow)、NoisyNet、オフライン RL、RLHF といった発展系を、本稿の“土台”にマッピングして復習することを推奨する。
- 理論基盤は マルコフ性 → マルコフ過程 → MRP → MDP → 誘導MRP の階段であり、MDP が中心モデルである。
- 価値は $V,Q,A$ と最適値 $V^*,Q^*$、目的関数は $J_\gamma,J_{\text{avg}}$ で、$\gamma$ は未来重視度のノブである。
- 探索と行動選択は ε-greedy/Softmax/UCB/Thompson/OFU を使い分け、実装は TD→SARSA/Q 学習、REINFORCE、Actor-Critic を軸に据えるべきである。
バックナンバーはこちら
深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第3版
徹底攻略ディープラーニングG検定ジェネラリスト問題集 第3版 徹底攻略シリーズ
ディープラーニングG検定(ジェネラリスト) 法律・倫理テキスト



コメント