論理思考の限界と再構築──集合論・群論で読み解く技術開発の構造

その他のエッセイはこちら

※本稿では集合論や群論といった数学的概念を思考の補助線として扱っている。
集合論に馴染みのない読者のために、文末に「付録：集合論の基本と導入のための問い」を設けた。
「集合とは何か」「写像とは何か」といった基礎を簡潔に確認できる内容である。必要に応じて参照されたい。

筆者について
想定読者
ロジカルシンキングの結果は「集合の一要素」に過ぎない
数理的思考の補助線：集合論と群論の基本概念
補足：抽象思考を直感で捉えるための比喩
ロジカルシンキングの構造：集合論的定式化
1. 事例：高齢者向けステアリング制御
チーム思考の構造：集合の合成と交差
1. 事例：制御仕様の議論
思考操作の構造：群論的定式化
1. 事例：制御アルゴリズムの設計と修正
構造的思考テンプレートの定義
ロジカルシンキングの代表的フレームワークとの対応
ロジカルシンキングの“背後”にある構造的思考
結論：ロジカルシンキングは「結果」ではなく「思考の構造」を再構築するツールである
付録A：集合論の基本と導入のための問い
付録B：集合論を活用した“質問力”の高め方

筆者について

筆者は自動車業界において、主に計測技術および推定アルゴリズムの開発に従事するエンジニアである。センサーデータの解析やモデルベース開発を通じて、現象の理解と予測に取り組む中で、論理的思考の有効性と限界の両面を実感してきた。

例えば、ある運転支援システムで「論理的にはこう動くはず」と設計した機能が、実際のドライバーからは「違和感がある」「使いにくい」といった予期せぬフィードバックを受けることがあった。このように、論理的思考で導き出した結論が、現実の複雑さの中で壁にぶつかる経験は少なくない。本稿では、そんなロジカルシンキングの「限界」と、それを乗り越える「可能性」について、集合論と群論という数学の視点から深く掘り下げていく。

なお筆者は、日々の技術開発において、集合論・群論・圏論といった抽象数学の枠組みを、明示的にではなく思考の裏側の構造として自然に用いていると感じている。これらの理論は、論理的思考の「道具」ではなく、「構造」そのものを捉えるための視座を提供してくれる。しかし、それをそのまま言語化しても、必ずしも聞き手に伝わるとは限らない。ゆえに本稿では、それらを前面に出すことなく、思考の補助線として静かに活用するという立場をとる。

なお、抽象的な構造を深く掘り下げることは、技術的な精度や汎用性を高めるうえで有効である。しかし、掘れば掘るほど表現は難しくなり、他者との共有が困難になる。ときに、掘らない方がキャッチーで伝わりやすいこともある。ゆえに筆者は、抽象的な構造を裏側に置きつつ、表面ではロジカルシンキングという“翻訳”を用いることで、思考の深さと伝達の軽やかさを両立させることを試みている。

想定読者

本稿は、技術開発や企画に関わる若手ビジネスパーソン（エンジニア、データアナリスト、製品企画担当など）を対象としている。論理的思考を日常的に用いながらも、現実とのギャップに悩む読者に向けて書かれている。

ロジカルシンキングの結果は「集合の一要素」に過ぎない

ロジカルシンキングで何かを導き出すとき、私たちは特定の「前提」を置き、その上で「論理的な推論ルール」を適用する。しかし、このプロセスで得られる結果は、あくまで「与えられた前提」と「適用したルール」という限定された枠組みの中での「可能性の一つ」に過ぎない。現実世界は常に変化し、私たちが把握している前提は往々にして不完全である。そのため、ロジカルシンキングの結論は、無数の「あり得る可能性」の中から選ばれた「たった一つの要素」に過ぎず、絶対的な真理ではないのだ。

例えば、高齢者向け運転支援システムの開発で、「センター保持力を強めれば安心感が増す」という仮説が立てられた。これは論理的には正しく見えるが、実際にユーザーからは「制御が強すぎて違和感がある」「自分の運転感覚と合わない」といった予想外のフィードバックが多く寄せられた。これは、「安心感」という前提集合の中に、「違和感」や「自分の運転感覚」といった考慮されていなかった要素が存在していたためである。この結果、最初の仮説は再構成を迫られることになった。

このように、ロジカルシンキングは「正しさ」を導くための手法であると同時に、「伝わりやすさ」を担保するための表現技法でもある。つまり、ロジカルであることは、思考の完成形ではなく、むしろ他者と共有するための“翻訳”に過ぎない。その背後には、より抽象的で構造的な思考──集合の全体像を捉え、操作の意味を問い直すような思考──が存在している。

数理的思考の補助線：集合論と群論の基本概念

本稿では、ロジカルシンキングの構造を集合論および群論の枠組みで定式化する。これらの数学的概念は、技術者が日常的に扱う「前提」「操作」「結果」といった思考プロセスを、抽象的かつ汎用的に表現するための有力なツールである。

集合論：思考の「材料」を扱う枠組み

集合論は、対象の集まり（集合）を定義し、それらの関係性や操作を記述する数学の分野である。技術開発における「前提条件」「観測結果」「仮説」などは、すべて集合として表現できる。

集合：ある性質を持つ要素の集まり（例：高齢者の運転特性）
冪集合 $\mathcal{P}(A)$：集合 $A$ のすべての部分集合（＝可能な組み合わせ）
合成 $\cup$：複数の集合を統合する操作（＝知識の統合）
交差 $\cap$：複数の集合に共通する要素を抽出する操作（＝共通認識）

集合論を用いることで、思考の前提や結果を構造的に整理し、チーム内での認識のズレや仮説の再構成を明示的に扱うことが可能となる。

群論：思考の「操作」を扱う枠組み

群論は、ある集合上で定義された操作（写像）が、特定のルールに従って構成される代数的構造を扱う数学の分野である。技術開発における「仮説構築」「反証」「修正」などの思考操作は、群論的にモデル化できる。

群の基本的な性質：

閉性：操作の結果も同じ集合に属する（＝思考が一貫性を保つ）
結合性：操作の括り方が結果に影響しない（＝思考の再構成が可能）
単位元（恒等操作）：何もしない操作が存在する（＝仮説を維持する）
逆元：ある操作を打ち消す操作が存在する（＝誤った仮説の撤回）

（※操作の順序が結果に影響しない性質は「可換性」と呼ばれ、アーベル群でのみ成立）

この枠組みにより、思考の流れを操作として捉え、仮説の構築から修正・撤回までを数学的に追跡可能なものとして扱える。

例：思考操作の流れ

仮説構築：$f$
修正：$h$
反証：$g = h \circ f$
撤回：$f^{-1} \circ f = \text{id}$

ただし、現実の思考では逆操作が常に存在するとは限らないことに注意が必要になる。情報の不可逆性や感情的要素が関与するため、群論はあくまで理想化されたモデルである。

群論の限界：理想化されたモデルとしての注意点

群論は、思考操作を構造的に捉えるための強力な枠組みである。しかし、現実の技術開発や意思決定の場面では、群論が前提とする理想的な条件が必ずしも成立するとは限らない。以下に、群論を思考モデルとして用いる際に意識すべき限界について述べる。

逆操作の不在：一度下した判断や設計を完全に巻き戻すことは困難であり、ユーザー体験や市場への影響は多くの場合、不可逆である。
単位元の曖昧性：「何もしない」ことが中立とは限らず、放置がリスクになる場合もある。
非可換性（順序依存）：思考操作の順序が結果に大きく影響する。群論では結合性は保証されるが、可換性は一般には成立しないため、順序依存の現象はモデル化しきれない。
閉性の破れ：外部から新たな情報が流入することで、前提集合そのものが拡張される。

このような限界を踏まえると、群論はあくまで「理想化された思考モデル」であり、現実の複雑な意思決定や設計プロセスを完全に記述するものではない。必要に応じて、より緩やかな代数的構造──たとえば、逆操作を持たない半群、単位元のみを持つモノイド、あるいは状態遷移を射として扱う圏論など──への拡張を検討することが、より現実的な思考支援につながる。

半群：操作の順序は守られるが、元に戻す操作（逆元）が存在しない構造。思考の流れが一方向である場面（例：仮説→テスト→修正）に適している。
モノイド：半群に「何もしない操作（単位元）」を加えた構造。初期状態の保持や、操作の中立性を扱う場面に有効。
圏論：対象（状態や概念）とそれらを結ぶ射（変換）を扱う枠組み。状態遷移やプロセスの流れを抽象的に捉えるのに適しており、システム設計やデータフローのモデル化に応用される。

こうした限界を意識することで、私たちは「ロジカルシンキングの限界」を単なる批判ではなく、「より深い構造への入り口」として捉えることができる。群論が破綻する場面こそが、圏論的な視点──対象と射の関係性を通じて、構造そのものを再定義する思考──の出番である。このように、抽象数学の理論は、ロジカルシンキングの“次の地平”を照らす灯台となり得る。

補足：抽象思考を直感で捉えるための比喩

集合論および群論は、技術的思考を構造的に捉えるための強力な抽象ツールである。しかしながら、読者の直感に訴えるためには、日常的な比喩を用いることが有効である。本節では、技術的思考を「レゴブロック」および「料理の工程」に例えることで、抽象的な構造をより身近に感じられるようにする。

レゴブロックで捉える仮説思考

仮説構築：前提条件（ブロック）を選び、論理的なルール（組み立て方）に従って構造物（仮説）を作る。
反証：完成した構造物に外力（ユーザーテスト）を加えると、脆弱な部分が崩れる。
修正：崩れた部分を補強し、新しいブロックを追加してより安定した構造にする。

この比喩は、集合 $A$ に推論規則 $R$ を適用して結論集合 $C$ を導く操作を、ブロックの組み立てと再構成として捉えるものである。

群論的操作の直感的理解：料理の工程による比喩

群論における操作は抽象的であるが、料理の工程に例えることで、技術者にとってより直感的に理解可能となる。ここでは、思考操作を「レシピに従って料理を作り、味見し、調整するプロセス」として捉える。

操作	料理工程	機能
$f$（仮説構築）	材料を選び、調理する	仮説を立案し、形にする
$h$（修正）	味見して調味料を加える	仮説を調整し、改善する
$g$（反証）	食べてみて「まずい」と判断する	仮説が現実に適合しないことを示す
$\text{id}$（恒等操作）	何も加えない	状況を維持する
$f^{-1}$（逆操作）	作った料理を捨てて材料に戻す	仮説を撤回し、初期状態に戻す

たとえば、「仮説を立てて、それを修正する」という一連の流れは、以下のように表現される。

$$
g=h\circ f
$$

これは、操作 $f$（仮説構築）に続けて操作 $h$（修正）を施すことで、結果的に操作 $g$（反証）と同様の状態に至る可能性があることを示している。すなわち、良かれと思って加えた修正が、かえって仮説の本質を損ない、否定されたかのような状況を生み出すことがあるということである。

この比喩は、思考の操作においても順序や組み合わせが結果に影響を与えることを示唆しており、群論の「合成」「逆元」「単位元」といった概念を日常的な感覚で捉えるための有効な手段となる。

集合論・群論・圏論の比喩による構造的理解

抽象数学の枠組みは、技術的思考を構造的に捉えるための強力な道具であるが、その抽象度ゆえに直感的な理解が難しい。そこで、集合論・群論・圏論をそれぞれエンジニアの実務に即した比喩で捉えることで、思考の補助線として活用しやすくなる。

集合論：技術要素の分類と関係性の可視化

集合論は、技術要素や仕様を「フォルダ分け」や「タグ付け」のように整理する枠組みである。センサーデータの種類、ユーザー属性、機能群などを集合として捉えることで、共通点（交差）や違い（差集合）を明示し、議論や設計の整理がしやすくなる。

例：
「この機能はAという集合に属するが、Bには含まれない」
「AとBの交差が、ユーザーにとっての共通価値である」

群論：処理や作業の操作構造と再構成可能性

群論は、処理や作業の「操作」とその組み合わせに関する構造を捉える枠組みである。アルゴリズムのステップや開発工程の順序が入れ替え可能か（可換性）、元に戻せるか（逆元）を考えることで、柔軟な設計や並行処理の可能性を見出すことができる。

例：
「この処理は順序を変えても結果が同じだから並列化できる」
「この修正は元に戻せるから、試験的に導入してもリスクが低い」

圏論：技術領域間の構造抽象と標準化

圏論は、異なる技術領域を圏として捉え、それらの間にある変換ルール（関手）を通じて、共通構造や標準化の可能性を探る枠組みである。これは、異なる言語間で意味を翻訳するような思考に近く、設計の抽象化と再利用性を高める。

例：
「この処理は画像でも音声でも同じ構造を持っている」
「この設計パターンは、異なる技術領域に関手として適用できる」

このように、集合論・群論・圏論は、技術者が日々直面する「分類」「操作」「関係性」の問題を抽象的に整理するための思考ツールであり、ロジカルシンキングの背後にある構造的思考を支える役割を果たしている。

ロジカルシンキングの構造：集合論的定式化

ロジカルシンキングとは、前提となる情報の集まりを「前提集合 $A$ 」とし、それに「推論ルール（思考の操作）の集まりを「推論規則集合 $R$ 」を適用することで、「結論の集まりを「結論集合 $C$ 」を導く操作であると定式化できる。

$$
C=R(A)\dots （前提集合 A に推論規則 R を適用した結果が結論集合 C になる）
$$

このとき、導かれる結論 $C$ は、常に前提 $A$ のあらゆる可能性（冪集合 $\mathcal{P}(A)$）の中から、特定の方法で選ばれた一部に過ぎない。つまり、ロジカルシンキングの結果は、私たちが考えうるすべての選択肢や組み合わせのほんの一部なのだ。

$$
C\subseteq \mathcal{P}(A)
$$

事例：高齢者向けステアリング制御

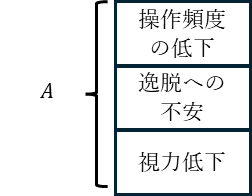
初期の前提集合（私たちが最初に持っていた情報）：

$$
A = { \text{視力低下(見えにくい)}, \text{逸脱への不安(車線からはみ出しそうという心配}, \text{操作頻度の低下(ハンドルを細かく動かせない)} }
$$

推論規則（これらの前提から導かれる論理）：

$$
R={視力低下\Rightarrow センター保持強化(中央に留まる力を強くする),操作頻度低下\Rightarrow自動補正強化(自動で修正する力を強くする)}
$$

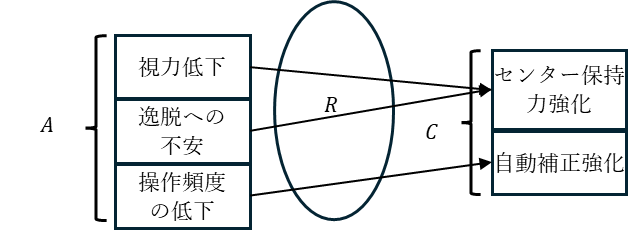
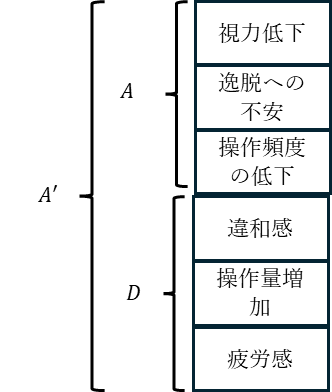
これにより、当初の結論集合 $C$ は「センター保持力強化」「自動補正強化」となった。しかし、ユーザーテストによって新たな観測集合 $D$ が得られた。これは、私たちの当初の前提にはなかった「現実からのフィードバック」である。

$$
D={違和感(しっくりこない),操作量増加(かえってハンドルを動かす量が増えた),疲労感(運転が疲れる)}
$$

この新しい情報 $D$ が加わることで、当初の前提集合は更新される。

$$
A\prime=A\cup D\dots(これまでの前提に新たな観測結果を追加)
$$

そして、更新された前提 $A\prime$ をもとに再度推論を行うことで、結論集合も更新される。

$$
C\prime=R(A\prime)={保持力緩和(センター保持力を弱める),応答の滑らかさ(ハンドルの反応をより自然にする)}
$$

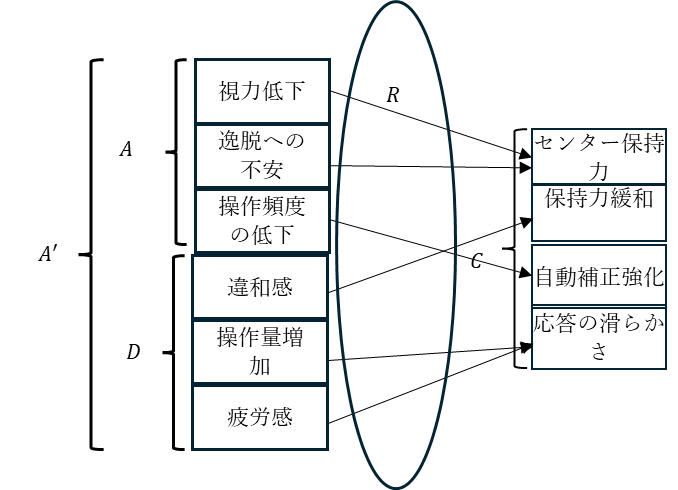
この事例は、ロジカルシンキングの結論が、新たな情報（現実）によっていかに変化し、再構築されるかを示している。

チーム思考の構造：集合の合成と交差

複数のメンバーがそれぞれ異なる前提集合 $A_1,A_2,\dots,A_n$ を持つ場合、チームとしての思考は以下のように構成される。

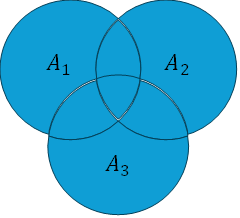
合成集合（知識の統合）:

$$
A_{\text{team}} = \bigcup_{i=1}^{n} A_i
$$

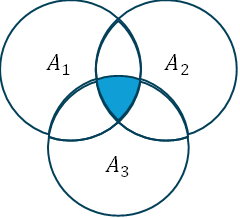
交差集合（共通認識の抽出）:

$$
A_{\text{consensus}} = \bigcap_{i=1}^{n} A_i
$$

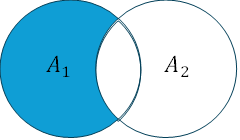
差集合（認識のズレ）：

$$
A_{\text{diff}}=A_1\setminus A_2
$$

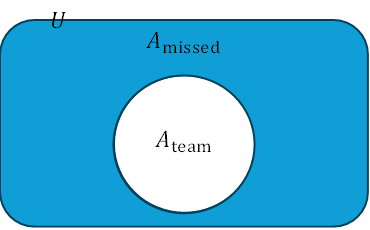
補集合（見落とし）：

$$
A_{\text{missed}}=U\setminus A_{\text{team}}
$$

これらを意識することで、議論の質が向上し、認識のズレや見落としを構造的に把握できる。

事例：制御仕様の議論

あるエンジニアは「制御は強めた方が安心感がある」と主張し、別のメンバーは「強すぎると操作が増えて疲れる」と反論した。両者の前提集合は異なるが、交差集合に「安心感と自然さの両立」が含まれていれば、議論は建設的に進む。

思考操作の構造：群論的定式化

思考操作を写像と捉えると、以下のような群構造が定義できる。

操作集合:

$$
G={f,g,h,\text{id}}
$$

ここで：

$f$：仮説構築（演繹）
$g$：反証（テスト結果による否定）
$h$：修正（仮説の調整）
$\text{id}$：恒等操作（何もしない変更）

合成規則の例：

$$
h\circ f=g
$$

単位元（恒等操作）:

$$
\text{id}\circ f=f
$$

逆元（誤りの是正）:

$$
f^{-1}\circ f=\text{id}
$$

事例：制御アルゴリズムの設計と修正

ある高齢者向け運転支援システムの開発において、以下のような前提集合 $A$ をもとに仮説を構築した：

$$
A={視力低下,逸脱への不安,操作頻度の低下}
$$

この前提に対して、仮説構築操作 $h$ を適用し、中間的な仮説集合 $B$ を得る：

$$
h:A\rightarrow B={センター保持力強化,自動補正強化}
$$

さらに、仮説集合 $B$ に対して結論導出操作 $f$ を適用し、制御仕様としての結論集合 $C$ を導出した：

$$
f:B\rightarrow C={制御パラメータの強化}
$$

この一連の操作は、合成写像として以下のように表される：

$$
g=h\circ f:A\rightarrow C
$$

しかし、ユーザーテストによって新たな観測集合 $D$ が得られた：

$$
D={違和感,操作量の増加,疲労感}
$$

これは、結論集合 $C$ に対する反証として機能し、写像 $g$ の妥当性に疑問を投げかけるものであった。すなわち、$g$ の結果が現実に適合しないことが示されたのである。

このとき、思考の流れは以下のような構造を持つ：

$$
A\overset{f}\longrightarrow B \overset{h}\longrightarrow C
$$
$$
A\overset{g=h\circ f}\longrightarrow C
$$

この式は、前提から仮説、結論、そして反証へと至る思考操作の流れを示している。重要なのは、反証によって得られた観測集合 $D$ をもとに、前提集合 $A$ を更新し、新たな仮説構築操作 $h’$ を定義することである。

$$
A^\prime=A\cup D
$$
$$
h^\prime:A^\prime\rightarrow B^\prime
$$
$$
f:B^\prime\rightarrow C^\prime
$$
$$
g^\prime=h\circ f^\prime:A^\prime\rightarrow C^\prime
$$

このように、思考操作は単なる一方向の流れではなく、反証によって再構成される動的な構造である。群論的な視点では、操作の合成や逆操作を通じて、仮説の撤回や再構築が可能であることが示されるが、現実の技術開発では、情報の不可逆性や感情的要素が関与するため、完全な逆操作は存在しないことも多い。

したがって、思考操作は理想的な群構造ではなく、半群やモノイド、あるいは圏論的な射の構造として捉える方が、現実に即したモデルとなる。

この事例は、ロジカルシンキングの限界と、それを乗り越える構造的思考の可能性を示している。仮説構築・反証・再構成という流れを、写像として明示的に捉えることで、技術開発における思考の透明性と柔軟性が高まるのである。

構造的思考テンプレートの定義

ロジカルシンキングの限界を乗り越えるためには、思考の構造そのものを明示的に捉える必要がある。本稿では、集合論・群論の枠組みを活用し、技術者の思考プロセスを以下の6つのステップに整理することで、「構造的思考テンプレート」として定式化する。

前提集合 $A$：思考の出発点となる情報群。仮説や判断の根拠。
推論規則 $R$：前提に対して適用される論理的操作。演繹・帰納など。
結論集合 $C$：推論の結果として導かれる仮説や仕様。
観測集合 $D$：現実から得られるフィードバック。反証や新情報。
更新された前提 $A’$：観測集合を加味して再構成された前提。
再推論による結論 $C’$：更新された前提に基づく新たな結論。

このテンプレートは、技術開発における仮説構築・検証・修正の流れを構造的に捉えるための思考支援ツールであり、ロジカルシンキングの背後にある構造的思考を可視化する役割を果たす。

さらに、このテンプレートは群論的な「操作」の視点でも捉えることができる。すなわち、各ステップは写像（操作）として表現可能であり、思考の流れは以下のような合成構造を持つ：

$f$：仮説構築（$A \rightarrow B$）
$h$：修正（$B \rightarrow B’$）
$g = h\circ f$：結論導出（$A \rightarrow C$）
$f^{-1}$：仮説撤回（$B \rightarrow A$）
$id$：恒等操作（状態維持）

このように、思考プロセスは単なる情報の整理ではなく、操作の連鎖としてモデル化できる。特に、仮説の構築・反証・修正・撤回といった流れは、群論的な合成・逆元・単位元の概念と対応しており、技術開発における思考の柔軟性と再構成力を高める。

ロジカルシンキングの代表的フレームワークとの対応

構造的思考テンプレートは、従来のロジカルシンキングのフレームワークとも親和性が高い。以下に、代表的な3つの思考フレーム──MECE、ピラミッド構造、So What / Why So──との対応関係を示す。

構造的思考項目	MECE（漏れなくダブりなく）	ピラミッド構造 / So What / Why So
① 前提集合 $A$	情報の網羅性と分類（MECEの基盤）	根拠・背景情報 / Why So（なぜそう考えるのか）
② 推論規則 $R$	分類に基づく論理展開	論理の流れ（演繹・帰納） / Why So（その結論に至る理由）
③ 結論集合 $C$	結論の明確化（MECEなアウトプット）	トップメッセージ（結論） / So What（だから何なのか）
④ 観測集合 $D$	MECEの再検証（漏れやズレの発見）	根拠の再評価 / Why So（現実とのギャップ）
⑤ 更新された前提 $A’$	情報の再分類・再構成	根拠の再整理 / Why So（新たな理由）
⑥ 再推論による結論 $C’$	再構成されたMECEな結論	新たなトップメッセージ / So What（新たな意味づけ）

この対応表は、構造的思考が単なる抽象的な理論ではなく、既存のロジカルシンキングの実践的枠組みと接続可能であることを示している。特に、MECEによる情報整理、ピラミッド構造による論理展開、So What / Why Soによる意味づけの明確化は、集合論・群論による構造的定式化と自然に接続する。

ロジカルシンキングの“背後”にある構造的思考

ロジカルシンキングは、思考の「結果」を他者に伝えるための形式である。しかし、その形式を自在に操る人々は、しばしばその背後にある構造──集合の全体像、操作の意味、関係性の抽象──を無意識に捉えている。それは、集合論的な分類、群論的な操作、圏論的な射の構造といった、抽象数学の枠組みに近い。

このような構造的思考は、必ずしも「集合論を使っています」「群論で考えています」と明言されることはない。むしろ、それを言語化せずとも自然に使いこなしている人ほど、ロジカルシンキングを超えた柔軟な思考ができている。本稿で紹介した集合論・群論の枠組みも、あくまでその一端に過ぎない。

重要なのは、ロジカルシンキングを「超える」ことではなく、「支える構造」として捉えることである。そうすることで、私たちは論理の限界にぶつかったとき、より深い構造に立ち戻り、思考を再構築することができる。

このような二層構造の思考は、技術者にとって実践的な態度である。抽象的な構造を掘り下げながらも、それを前面に出さず、ロジカルな形式で表現することで、思考の本質を損なうことなく他者との共有を可能にする。これは、単に「伝える」ための工夫ではなく、掘ったうえで掘っていないように見せるという、高度な思考と表現の融合である。

結論：ロジカルシンキングは「結果」ではなく「思考の構造」を再構築するツールである

集合論や群論の視点から見ると、ロジカルシンキングが導き出す「結論」は、与えられた前提の中での「可能性のひとかけら」に過ぎない。現実が常に変化し、新たな情報（集合の要素）が加わることで、私たちの前提は更新され、それに伴い結論も柔軟に変化していく必要がある。

したがって、ロジカルシンキングの真の価値は、特定の「結果」を導き出すことだけにあるのではない。むしろ、私たちの思考の「前提」や「操作」を集合として明確にし、チームで共有し、そして変化に応じて「再構成」できることにこそ、その本質的な価値がある。

この数学的な思考構造を理解することで、私たちは以下のような行動に繋げることができる。

前提の「不完全さ」を認識する: 自分の思考の前提が常に完全ではないことを自覚し、新しい情報（新たな集合の要素）を取り入れる柔軟性を持つ。
- 仮説を立てる前に、前提集合を書き出し、見落としがないか確認する。
「共通認識」を可視化する: チームメンバーとの議論において、何が共有されている前提（集合の交差）で、何が認識のズレ（集合の差分）なのかを意識的に把握し、議論の質を高める。
- チームで議論する際、交差集合と差集合を意識して認識のギャップを埋める。
思考プロセスを「操作」として捉える: 仮説の構築、反証、修正といった思考の流れを意識的な「操作」として捉え、過去の意思決定を客観的に見つめ直し、改善に繋げる。
- 仮説構築・反証・修正の流れを操作として記録し、逆操作の可能性も検討する。

技術開発の現場において、ロジカルシンキングは強力な武器である。しかし、それが現実という複雑な集合の一部に過ぎないことを理解し、その思考構造を柔軟に「再構成」できる能力こそが、不確実な未来を切り拓くための重要な鍵となるだろう。

付録A：集合論の基本と導入のための問い

本稿では集合論を思考の補助線として活用しているが、集合論に馴染みのない読者も多いと想定される。そこで、集合論の全体像を認識するための「問い」と簡単な説明を以下に示す。

集合とは何か？

問い：「集合とリストの違いは？」
説明：集合は「順序を持たず、重複を許さない」要素の集まりである。
例：

$$
A=\{1,2,3\},\ B=\{3,2,1\}\dots(AとBは同じ集合)
$$

集合をどう組み合わせるか？

問い：「AとBを合わせると？共通部分は？」
説明：

和集合：$A \cup B$（AまたはBに属する要素）
積集合：$A \cap B$（AとBの両方に属する要素）
差集合：$A \setminus B$（AにあってBにない要素）

写像（関数）とは何か？

問い：「写像を一言でいうと？」
説明：集合Aの要素を集合Bの要素に対応付けるルール。

$$
f:A\rightarrow B
$$

これは「入力→変換→出力」という関数のイメージに近い。
ここで、$A$ を定義域、$B$ をコドメイン（値域を含む集合）と呼ぶ。コドメインは重要である。なぜなら、同じ $A$ の要素に対しても、コドメインを変えると写像の意味が変わるからである。

写像の性質

単射（injective）：異なる要素が同じ像を持たない写像
- $a_1\neq a_2\Longrightarrow f(a_1)\neq f(a_2)$
全射（surjective）：$B$ のすべての要素に対応する $A$ の要素が存在する
- $\forall b\in B,\exists a \in A:f(a)=b$
全単射（bijective）：単射かつ全射である写像
- $A$ と $B$ の要素が一対一対応する。この場合、逆写像 $f^{-1} : B \to A$ が存在する。

例

集合
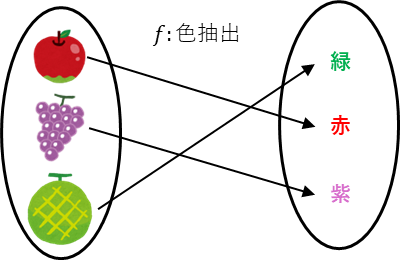
- $A = \{\text{リンゴ}, \text{ブドウ}, \text{メロン}\}, \quad B = \{\text{赤}, \text{紫}, \text{緑}\}$
全単射の例
- $f(\text{リンゴ}) = \text{赤}, \;f(\text{ブドウ}) = \text{紫}, \;f(\text{メロン}) = \text{緑}$
  - $A$ と $B$ が一対一対応しているので全単射である。
全射の例（イチゴを追加）
- $A = \{\text{リンゴ}, \text{ブドウ}, \text{メロン}, \text{イチゴ}\}$
- 「イチゴ」も「赤」に分類した場合、
  - $f(\text{リンゴ}) = \text{赤}, \;f(\text{イチゴ}) = \text{赤}$
    - $B$ の要素（赤・紫・緑）はすべて対応しているので全射であるが、単射ではない。
非全射の例（さらにミカンを追加）
- $A = \{\text{リンゴ}, \text{ブドウ}, \text{メロン}, \text{イチゴ}, \text{ミカン}\}$
- 「ミカン」は「橙」に分類するが、$B$ に「橙」が存在しない場合、$f(\text{ミカン}) \text{ は未定義}$
  - この場合、写像は全射でも単射でもなくなる（定義域の要素に対応する像が欠けるため）。

冪集合とは？

問い：「A={1,2}の冪集合は？」
説明：

$$
\mathcal{P}(A)=\{\emptyset,\{1\},\{2\},\{1,2\}\}
$$

すべての部分集合の集まりを冪集合という。

集合論を知ると何が嬉しい？

問い：「なぜ集合論を知ると役立つのか？」
説明：

前提条件や選択肢を「集合」として整理できる。
和集合＝知識統合、積集合＝共通認識、差集合＝認識のズレ。
技術開発や仕様検討で、議論の構造を明示できる。

付録B：集合論を活用した“質問力”の高め方

ステップ：質問を構造化する

全体像を把握する
- セミナーや議論のテーマを「全体集合 $U$」として意識する。
集合を認識する
- どんな要素群（集合）があるかを抽出する。
集合を識別する
- 各集合に名前を付け、役割を明確化する。
集合関係を分解する
- 集合同士の関係を写像として表現する。
欠損を見つける
- 写像が片方向のみ、逆写像が存在しないなどの構造的な抜けを探す。
言語化して質問する
- 「逆写像は存在しないのか？」など、構造の欠損を突く質問を提示する。

具体例：人事評価セミナー「成果と評価」

集合
- 成果集合 $P$
- 評価集合 $E$
写像
- $f: P \to E$（成果 → 評価）
気づき
- 逆写像 $f^{-1}$ は定義されていない。
質問
- 「期待する評価を先に置き、そこから成果を設計する方式はあり得ないか？」
- 例えば：「評点4を取得するには、XXXな成果をあげる必要がある」ことを先に伝える。
  - これは「逆写像の存在可能性」を問う質問。

なぜ有効か？

単なる「質問」ではなく、構造の欠損を突く質問になる。
さらに、集合論を使うことで、質問の焦点が明確になる。

応用のヒント

逆写像が存在しない場合でも、「評価から成果への対応を部分的に定義できないか」を考えると、新しい発想につながる。
例えば、「期待する評価を先に設定し、それに対応する成果を提示する」という逆方向の視点は、集合論的な問いから生まれる。
離散化された評価集合の背後に連続的なスコア空間を仮定し、$P$ とそのスコア空間との間で全単射を定義することで、思考の柔軟性を高める。

評価の離散化と全単射の議論

実務における評価は、しばしば5段階やA/B/Cといった離散的なカテゴリーで表現される。この場合、成果集合 $P$ から評価集合 $E$ への写像 $f : P \to E$ は、同じ評価に複数の成果が対応するため、全単射にはなり得ない。しかし、評価の背後には連続的なスコア（例：満足度や達成度の実数値）が存在すると仮定すれば、$P$ とスコア空間との間に全単射を定義することが可能である。この視点は、離散化の前段階にある連続関数を意識することで、設計や分析の柔軟性を高めるものである。