https://www.simulationroom999.com/blog/jdla-deep-learning-for-general-2020-1/
はじめに
ディープラーニングは様々なテクニックの集合体と言える。
ここでは以下の代表的なテクニックを記載する。
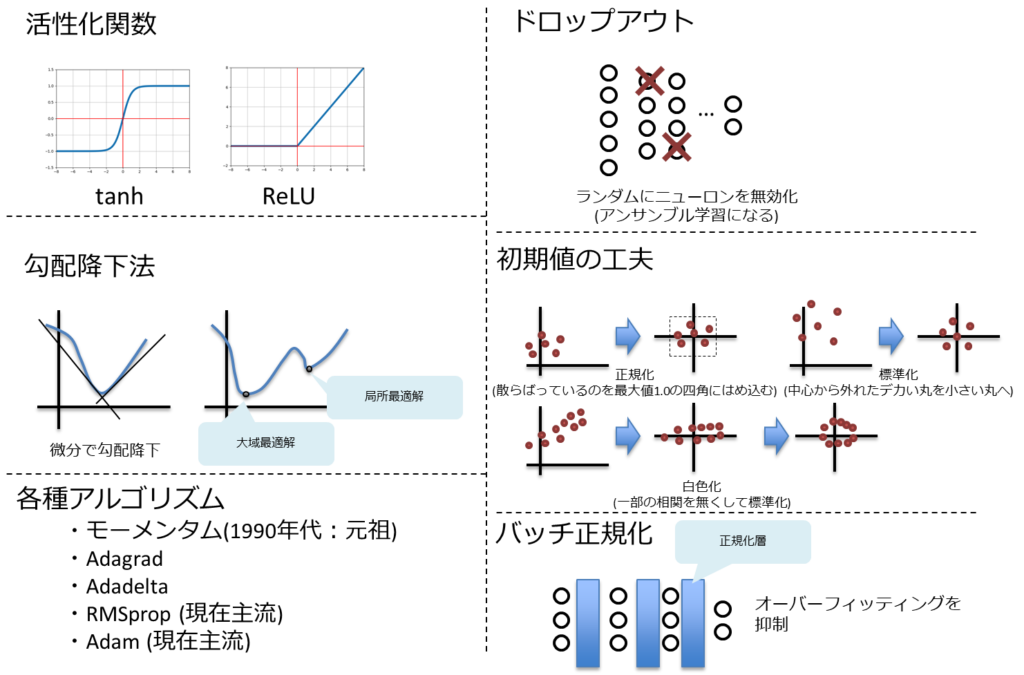
活性化関数
勾配消失の問題の最大の原因はシグモイド関数の導関数の最大値が0.25と小さいことであった。
よって、このシグモイド関数を別の物に置き換えることでこの問題が回避できるのでないか?
というアプローチの元、シグモイド関数を設置していた部分を差し替える発想が出てくる。
この差し替え可能な関数を活性化関数と呼ぶ。
最終的な出力はシグモイド関数が望ましいが、隠れ層はそうでもない。
tanh関数
正式名称はハイパボリックタンジェント関数。
関数の特性はシグモイド関数に似ている。
違いは、値の範囲が0,1ではなく、-1,1の範囲になる。
これにより導関数も、最大値が1となり、勾配消失の抑制効果が期待できる。
ReLU(Rectified Linear Unit)関数
x<0の時は0、0<xの時はリニアになる関数。
これの導関数はx<0の時は0、0<xの時は1となる。
0<xの時の学習効率は高いが、x<0の時は勾配消失し易くなる。
これを改良したものにLeakyReLUのようにx<0の時も緩やかな傾きを持った活性化関数も存在する。
また、その傾きを学習によって最適化するParametric ReLUや複数の傾きをランダムに試行するRandomized ReLUなども登場している。
学習率の最適化
勾配降下法
機械学習の目的は「モデルの予測値と、実際の値との誤差をなくすこと」にある。
誤差関数を最小化する「関数の最小化問題」がある。
関数の最小化を求めるには微分が最適であり、それぞれの層の重みで誤差関数を偏微分した値が0になるように求める。
ニューラルネットワークでは、各パラメータ(重み)に対して勾配降下法を適用して最適解を求める。
勾配降下法とは、勾配に沿って降りていくことで解を探索する手法であり、微分値こと接線の傾きで勾配の向きを判断する。
また、ディープラーニングのようにパラメータ数が多いと訓練データを何回も繰り返して学習させないとパラメータをうまく学習できない。繰り返し学数を実施していくが、この繰り返しの単位をエポックと呼ぶ。
勾配を0にするにあたって、以下のパラメータが必要となる。
「勾配に沿って一度にどれだけ降りていくか」
これを学習率と呼び、最初は大きく、最後は小さく微調整する値となる。
問題と改善方法
勾配降下法を使用して、誤差関数が最も小さく部分を解とした場合、以下の問題が発生する。
傾きが0になる部分が2か所以上あるケースでは「見せかけの最適解」であるかどうかを見抜くことができない。
これは「局所最適解」と「大域最適解」という言葉で表される。
局所最適解とは、「見せかけの最適解」であり、大域最適解とは、複数ある局所最適解の中に於いての本当の最適解となる。
対策としては以下がある。
- 学習率の値を大きく設定
- 適切なタイミングで学習率の値を小さくしていく
さらに別の問題点としては以下がある。
3次元空間で、とある次元では最適解であるが、他の次元では極大になる鞍点に入り込む可能性がある。
また、この鞍点近辺は勾配が小さいことが多く、抜け出すことが困難。
(これをプラトーと呼ぶ)
対策としては、「どの方向に沿って勾配を進んでいるときに学習率を大きく(あるいは小さく)すべきかを考える」アルゴリズムを使用することになる。
以下の学習アルゴリズムが代表的
- モーメンタム(1990年代に提唱)
- Adagrad
- Adadelta
- RMSprop (現在主流のアルゴリズム)
- Adam (現在主流のアルゴリズム)
更なるテクニック
ドロップアウト
ディープニューラルネットワークは複雑な関数を表現できるため訓練データに対し、過敏な反応をしてオーバーフィッティングし易くなっている。
これの対策としてドロップアウトという手法が使われる。
ドロップアウトはエポック毎にランダムにニューロンを除外させる手法になる。 これはアンサンブル学習と同義になる。
early stopping
early stoppingとは、学習を進めて行く中でテストデータに対する誤差関数が右上がりになり始めた時点で学習を止めることを指す。ジェフリー・ヒルトンはノーフリーランチ定理を意識し、このテクニックのことをBeautiful FREE LUNCHと言った。
あらゆる問題で性能の良い汎用最適化戦略は理論上不可能。
ノーフリーランチ定理
初期値の工夫
以下のバリエーションがある。
- 正規化
- データ全体を調整する処理で、各特徴量を0~1の範囲に変換する処理。
- 標準化
- 特徴量を標準正規分布に従うように変換する。
- 白色化
- 各特徴量を無相関化した上で標準化する。
- 重みの初期値を工夫
- 乱数にネットワークの大きさに合わせた適当な係数をかける。
- シグモイド関数に対してはXavierの初期値。
- ReLU関数に対してはHeの初期値。
バッチ正規化(batch normalization)
各層に伝わってきたデータを、その層でまた正規化する手法をバッチ正規化と呼ぶ。
各層において活性化関数をかける前に伝播してきたデータを正規化することでオーバーフィッティングしにくくなる。
まとめ
- 勾配降下法で楽に誤差関数を0に近づける手法が主流になった。
- 活性化関数のバリエーションを増やすことで勾配を作りやすくした。
- 局所最適解や鞍点に陥らないような学習アルゴリズムが登場。
- さらに精度を高めたり、精度が上がることによるオーバーフィッティング抑制など手法自体も微調整される状況となった。




コメント