ディープラーニング、機械学習の基礎数学

https://www.simulationroom999.com/blog/jdla-deep-learning-for-general-2020-1/

微分
1. 微分係数の定義
2. 導関数の公式
偏微分
ベクトル、行列の演算
統計学
相関

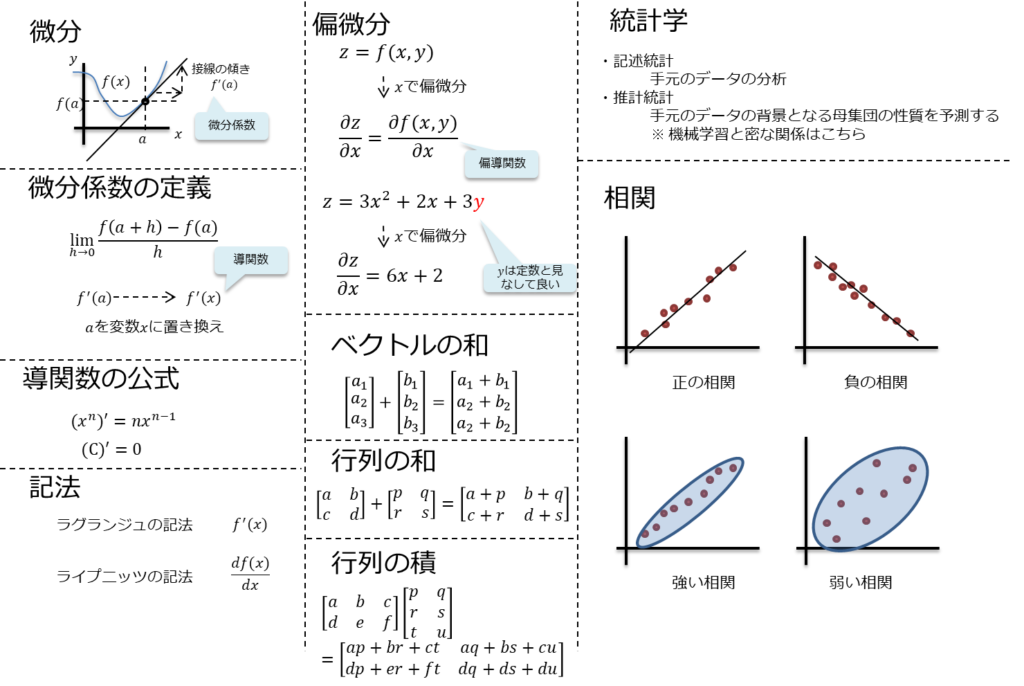
微分

関数$y=f(x)$の接線を$x=a$に於いて引き、
その傾きを$y=f(x)$の$x=a$に於ける微分係数と呼び、$f´(a)$と表す。

微分係数の定義

$$\lim_{h \to 0} \frac{ f(a+h) – f(x) }{h}$$

$f´(a)$の$a$を変数$x$に置き換えた関数$f´(x)$を導関数と呼ぶ。

導関数の公式

$$(x^n)´=nx^{n-1}$$
$$C´=0$$

尚、以下2つは記法が異なるが$f(x)$の微分を表現している。

ラグランジュの記法
- $f(x)´$
ライプニッツの記法
- $\frac{df(x)}{dx}$

偏微分

$f(x,y)$のような多変数関数に対しては通常の微分(常微分)では演算が困難。
そこで、微分する次元を指定する偏微分が用いられる。
3次元空間として、$x,y$の値から$z$を求めたい場合は以下の式になる。
$$z=f(x,y)$$
そして、$x$の変化が$z$の変化を特定したい場合は以下で表現する。
$$\frac{\partial{z}}{\partial{x}}=\frac{\partial{f(x,y)} }{\partial{x}}$$
これを偏導関数と呼ぶ。

ベクトル、行列の演算

ベクトルの和

$${\begin{bmatrix} a_1 \\ a_2 \end{bmatrix}}+ {\begin{bmatrix} b_1 \\ b_2 \end{bmatrix}}= {\begin{bmatrix} a_1 + b_1 \\ a_2 + b_2 \end{bmatrix}} $$

行列の和

$${\begin{bmatrix} a & b \\ c & d \end{bmatrix}}+ {\begin{bmatrix} p & q \\ r & s \end{bmatrix}}= {\begin{bmatrix} a+p & b+q \\ c+r & d+s \end{bmatrix}} $$

行列の積

$${\begin{bmatrix} a & b & c \\ d & e & f \end{bmatrix}}+ {\begin{bmatrix} p & q \\ r & s \\ t & u \end{bmatrix}}= {\begin{bmatrix} ap+br+ct & aq+bs+cu \\ dp+er+ft & dq+es+fu \end{bmatrix}} $$