MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その103【フーリエの積分公式④】
MATLAB,Python,Scilab,Julia比較 第5章 その104【フーリエの積分公式⑤】
を書き直したもの。
フーリエの積分公式を求める話の続き。
以下の話について。
- 離散的な係数導出が、連続的な角周波数導出に近付く。
- フーリエの積分公式を導出。
【再掲】角周波数ωとその刻みであるΔωで表現しなおした式
前回の角周波数ωとその刻みであるΔωで表現しなおした式を再掲
\(
\displaystyle f(x)=\sum_{n=-\infty}^\infty \Big\{\frac{1}{2\pi}\int_{-L}^Lf(t)^{-i\omega_n t} \,dt\Big\}e^{i\omega_n x}\Delta\omega
\)
これにより、離散的な係数導出を、連続的な角周波数導出に近づけていく。
完全に連続にする
前回は\(\Delta\omega\)という刻みだったが、
これでもまだ離散的な状態。
\(\Delta\omega\to 0\)とすれば連続と言える。
ついでに、\(L\to\infty\)とすると、変換元波形全域になる。
いわゆる極限。
以下の式になる。
\(
\displaystyle f(x)=\lim_{\begin{eqnarray}\Delta\omega\to 0\\L\to\infty\end{eqnarray}}
\sum_{n=-\infty}^\infty \bigg\{ \frac{1}{2\pi}\int_{-L}^L f(t)e^{-i\omega_n t}\,dt \bigg\}e^{i\omega_n x}\Delta\omega
\)
\(\lim\)のところとか、どう書くか悩んだ・・・。。
MathJaxでの数式の書き方をむっちゃ試行錯誤した。
これで連続になったかと言えば、なった。
少なくとも式の意味としては連続になった。
しかし、あまり一般的な書き方ではない。
これを一般的な書き方へ変更する必要がある。
区分求積法とリーマン積分
ここで区分求積法を用いる。
積分を求める際の最もシンプルな近似法。
図にするとこんなイメージになる。
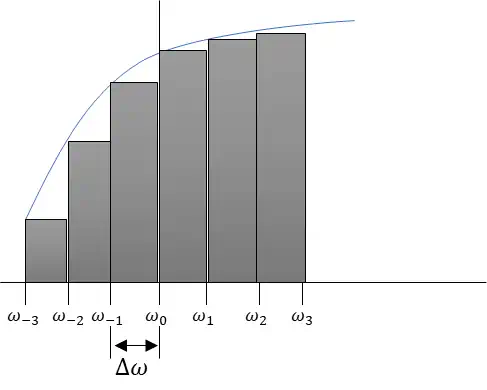
高校数学の積分の話の時に見たと思う。
リーマン積分の説明の時にも出てくる図でもある。
区分求積法とリーマン積分はとても似ているが、じつはちょっと違う。
区分求積法の\(\Delta x\)が0に近付くときの極限とした場合にリーマン積分になる。
ここでポイントとなるのは、
区分求積法の段階では離散的だが、リーマン積分にすると連続的になるってところ。
式で表現すると以下が成立するという話になる。
\(
\displaystyle\lim_{\Delta x\to0}\sum_{n=-\infty}^{\infty}G(x_n)\Delta x=\int_{-\infty}^{\infty}G(x)\,dx
\)
離散から連続へ
とすると、さっきの極限を用いた式の\(\displaystyle\sum\)が\(\displaystyle\int\)になるってことがわかる。
式にすると以下になる。
\(
\displaystyle f(x)=\int_{-\infty}^{\infty}\bigg\{ \frac{1}{2\pi}\int_{-\infty}^{\infty}f(t)e^{-i\omega t}\,dt \bigg\}e^{i\omega t}\,d\omega
\)
これが「フーリエの積分公式」と呼ばれるもの。
あとになるとわかることだが、逆フーリエ変換と同じ式ともいえる。
この式を示しているのは、以下の式が、
複素指数関数との積を2回行っても成立するというところ。
\(
f(x)=f(t)
\)
演算したはずなのに変化しない。
不思議な現象。
まぁ、これが変換と逆変換ができることの証明とも言えるわけになる。
まとめ
- Δωで刻みにしたので、極限を利用して連続系へ。
- 数式上は連続ではあるが、一般的な表現ではない。
- 区分求積法とリーマン積分について。
- フーリエの積分公式を導出した。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント