継承・ポリモーフィズム = 行列の差し替え・切り替え
オブジェクト指向の中核にある継承やポリモーフィズムも、線形代数的に解釈できる。
継承:変換行列の拡張
継承は、ソフトウェア設計において「子クラスが親クラスの構造や振る舞いを引き継ぎつつ、必要に応じて変更や拡張を行う」という概念として理解されている。これを線形代数的に表現するならば、以下の関係式が直観的に用いられることが多い。
$$
A_{child} = A_{parent} + \Delta A
$$
ここで $\Delta A$ は、親クラスからの差分としての追加的な変換成分を表す。
だしこのときの「+」は、 $A_{parent}$ を完全に上書きする操作ではなく、構造的に保持したまま $\Delta A$ を加えるような意味合いを持つ。すなわち、継承とは「ベースとなる変換行列 $A_{parent}$ を残しつつ、そこに差分変換 $\Delta A$ を付加する」ような構造の拡張操作として捉えるべきであり、単純な線形加算や置換操作とは区別される必要がある。
この視点に立つと、子クラスは親クラスの変換を部分的に再利用しながら、独自の変換(振る舞いや状態)を追加していることになる。変換行列としてのオブジェクトの再解釈は、こうした拡張可能な構造体としての側面を明示的に捉えることに寄与する。
例:継承 = 行列の差分
import numpy as np
# 「オブジェクト」としての変換行列
class LinearObject:
def __init__(self, matrix):
self.matrix = matrix
def apply(self, vector):
return self.matrix @ vector # Apply linear transformation
# 親クラスの変換行列(単位行列)
parent_matrix = np.eye(2)
# 子クラスの差分行列(スケーリング)
delta_matrix = np.array([
[2, 0],
[0, 1]
])
# 入力ベクトル
x = np.array([[1], [0]])
# 子クラスの行列 = 親 + 差分
child_matrix = parent_matrix + delta_matrix
# 子オブジェクト
scaler = LinearObject(child_matrix)
# 同じ入力に対して異なる出力
print("親オブジェクト:\n", LinearObject(parent_matrix).apply(x))
print("子オブジェクト:\n", scaler.apply(x))親オブジェクト:
[[1.]
[0.]]
子オブジェクト:
[[3.]
[0.]]ポリモーフィズム:行列の切り替え
ポリモーフィズムは、同一の入力に対して異なる変換行列を適用することで、異なる出力を得る構造である:
$$
y_1 = A_1 \cdot x,\quad y_2 = A_2 \cdot x
$$
これは、動的ディスパッチの数理的表現と捉えることができ、実行時に適切な変換行列を選択することで柔軟性と抽象性を両立した設計が可能となる。
例:ポリモーフィズム = 行列の切り替え
# 「オブジェクト」としての変換行列
class LinearObject:
def __init__(self, matrix):
self.matrix = matrix # 変換行列
def apply(self, vector):
return self.matrix @ vector # 線形変換を適用
# 2つの異なる変換行列
A1 = np.array([[1, 2], [0, 1]])
A2 = np.array([[0, 1], [-1, 0]])
# 入力ベクトル
x = np.array([[1], [0]])
# 同じ入力に対して異なるオブジェクトを適用
obj1 = LinearObject(A1)
obj2 = LinearObject(A2)
print("A1による変換:\n", obj1.apply(x))
print("A2による変換:\n", obj2.apply(x))A1による変換:
[[1]
[0]]
A2による変換:
[[ 0]
[-1]]非線形関数 = 条件分岐の抽象化
線形変換のみでは表現できない処理も、非線形関数を挿入することで対応可能となる:
$$
Y = f(A \cdot X)
$$
この構造は、ソフトウェアにおける if や switch のような条件分岐を、連続的な関数として抽象化することを可能にする。
たとえば、ReLU(Rectified Linear Unit)関数:
$$
f(x) = \max(0, x)
$$
※ReLU(Rectified Linear Unit)は、入力が0以下なら0、それ以外はそのまま返す関数。ニューラルネットワークでよく使われ、条件分岐のような役割を果たす。
これは、条件分岐を滑らかに連続化したものと見なすことができる。sigmoidやtanhなども同様に、非線形な振る舞いを連続的に表現するための関数である。
このような非線形関数の導入により、複雑な状態遷移や条件分岐を数式として一貫して扱うことが可能となり、設計の明快さと解析可能性が向上する。
例:if文による条件分岐 vs ReLU関数
import numpy as np
import matplotlib.pyplot as plt
# 明示的な条件分岐(if文)
def step_function(x):
return np.array([1 if xi > 0 else 0 for xi in x])
# 非線形関数:ReLU(連続的な条件分岐の抽象化)
def relu(x):
return np.maximum(0, x)
# 非線形関数:sigmoid(より滑らかな分岐)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 入力ベクトル
x = np.linspace(-5, 5, 200)
# 出力
y_step = step_function(x)
y_relu = relu(x)
y_sigmoid = sigmoid(x)
# 可視化
plt.figure(figsize=(10, 6))
plt.plot(x, y_step, label='Conditional branching by if statement(step)', linestyle='--')
plt.plot(x, y_relu, label='ReLU (nonlinear function)')
plt.plot(x, y_sigmoid, label='Sigmoid (smooth bifurcation)')
plt.title("Comparison of conditional branches and nonlinear functions")
plt.xlabel("x")
plt.ylabel("Outpu")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()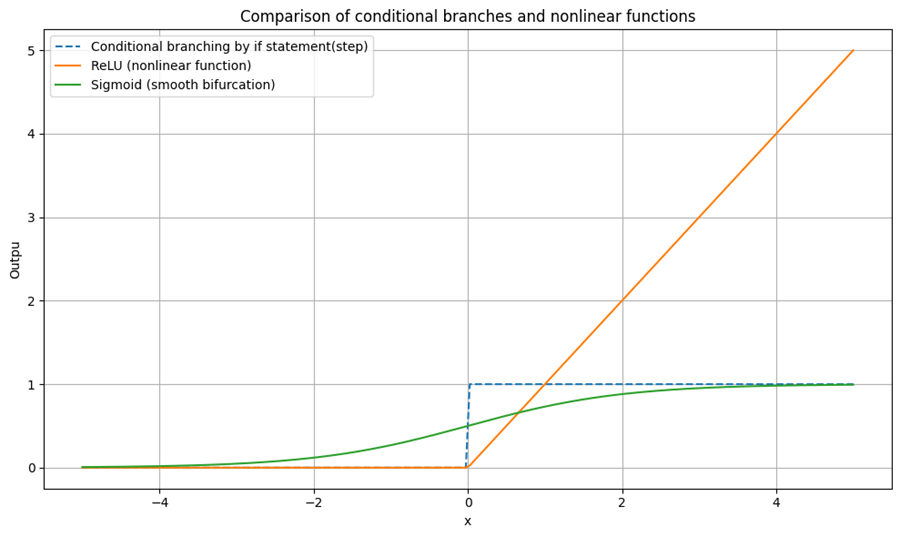


コメント