Attention機構の線形代数的解釈とオブジェクト指向的再構成
Attentionは、入力された情報の中から「どこに注目すべきか」を学習する仕組み。特に自然言語処理においては、文章中の単語同士の関係性を動的に捉えるために使われる。Transformerというモデルの中核をなす技術。
TransformerにおけるSelf-Attentionは、線形代数と非線形関数の組み合わせによって、情報の動的な関係性を計算する仕組みである。
Attentionの基本構造:
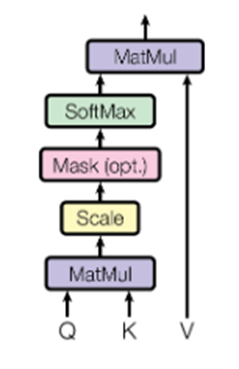
$$
\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\cdot V
$$
※この式は、Query(注目したい情報)とKey(識別子)の類似度を計算し、Value(実際の情報)を重み付きで合成する操作となる。自然言語処理で重要な役割を果たす。
これは入力間の関係性を重み付きで再構成する操作である。ここで、Query(Q)、Key(K)、Value(V)はそれぞれベクトルであり、入力トークンごとに生成される。
オブジェクトとしてのQuery/Key/Value
この構造は、オブジェクト指向的に以下のように解釈できる:
- Query:注目したい情報の特徴(目的)
- Key:各入力の識別子(属性)
- Value:実際に取り出す情報(状態)
QueryオブジェクトがKeyオブジェクト群に対して「どれに注目すべきか」を計算し、Valueから情報を抽出する。この構造は、オブジェクト間のメッセージパッシングや依存関係の動的構築と類似している。
import numpy as np
import matplotlib.pyplot as plt
# Keyオブジェクトの定義(識別子ベクトル)
class Key:
def __init__(self, vector):
self.vector = vector
# Valueオブジェクトの定義(取り出す情報ベクトル)
class Value:
def __init__(self, vector):
self.vector = vector
# Queryオブジェクトの定義(注目したい特徴ベクトル)
class Query:
def __init__(self, vector):
self.vector = vector
# Attention重みの計算(QueryとKeyの類似度)
def compute_attention_weights(self, keys):
scores = np.array([np.dot(self.vector, key.vector) for key in keys]) # 内積によるスコア
exp_scores = np.exp(scores - np.max(scores)) # softmaxのための安定化
attention_weights = exp_scores / np.sum(exp_scores) # softmax正規化
return attention_weights
# Attention重みを使ってValueを合成
def retrieve_values(self, keys, values):
attention_weights = self.compute_attention_weights(keys)
output = sum(w * v.vector for w, v in zip(attention_weights, values)) # 重み付き合成
return output, attention_weights
# サンプルのKeyとValueを作成
keys = [Key(np.array([1, 0, 0])), Key(np.array([0, 1, 0])), Key(np.array([0, 0, 1]))]
values = [Value(np.array([0.5, 0.2, 0.1])), Value(np.array([0.1, 0.7, 0.3])), Value(np.array([0.3, 0.4, 0.6]))]
# Queryを定義
query = Query(np.array([0.2, 0.8, 0.1]))
# 出力ベクトルとAttention重みを計算
output_vector, attention_weights = query.retrieve_values(keys, values)
# Attention重みの可視化
plt.figure(figsize=(6, 4))
plt.bar(range(len(attention_weights)), attention_weights, tick_label=[f"Key {i+1}" for i in range(len(keys))])
plt.title("Attention Weights (Query vs Keys)")
plt.xlabel("Keys")
plt.ylabel("Attention Weight")
plt.tight_layout()
plt.show()
# 出力ベクトルの表示
print("Output vector:", output_vector)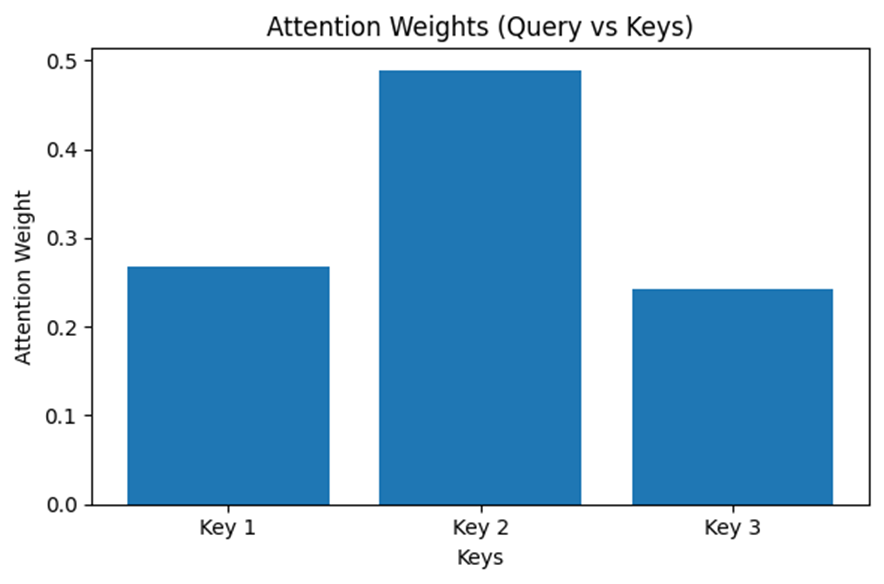
Output vector: [0.25588256 0.4930077 0.31917147]Self-Attentionと自己参照
オブジェクト指向における self と、Transformer系モデルにおける Self-Attention。これらは一見異なる領域に属する構造であるが、共に「自己を文脈の中で再評価・再構成する」という点で共通している。本節では、この「自己参照の構造」を線形代数的視点から接続し、両者に共通する抽象操作を明らかにする。
OOPにおける self:型文脈に依存する自己再評価
オブジェクト指向において self は、クラス内から自分自身のメソッドや属性にアクセスするための参照である。しかしそれは単なる静的な参照ではない。継承階層において self.do() と記述した場合、self の実体(=実行時型)に応じて適切な do() 実装が動的に選択される。
これは、self が「現在の型文脈において意味を持つ振る舞いの射影」として機能していることを意味する。self は、自身が属するクラスという文脈に応じて、定義済みの振る舞い(基底)から有効な成分を選択・再構成しているとも言える。これはまさに「基底空間の変換と射影」として理解可能である。
Self-Attentionにおける自己参照:意味文脈に依存する自己再構成
一方、Self-Attentionでは、系列中の各要素が自身を含む入力全体に対して注意(Attention)を行う。数式としては以下のように表される:
$$
\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})\cdot V
$$
ここで $Q=XW^Q,K=XW^K,V=XW^V$ として、入力 $X$ を線形変換したベクトル間の類似度を計算し、重み付き和として自己ベクトルを“再構成”している。つまり、Self-Attentionは、全体文脈を通して「自己の重要性・意味」を再評価する構造であり、「注意重み」を通じて情報をフィルタリングし直す操作とみなせる。
この構造は、入力系列を張るベクトル空間における動的な射影演算としても解釈できる。Attentionは「どの軸が意味的に重要か」を学習的に選び取るため、自己ベクトルは常に「文脈によって定義され直された基底」によって表現される。
なお、Self-Attentionにおける Query(Q)、Key(K)、Value(V)は、単に同一の入力系列から取り出されるわけではなく、それぞれ異なる線形変換を通じて生成される。すなわち、以下のような構造が前提となる:
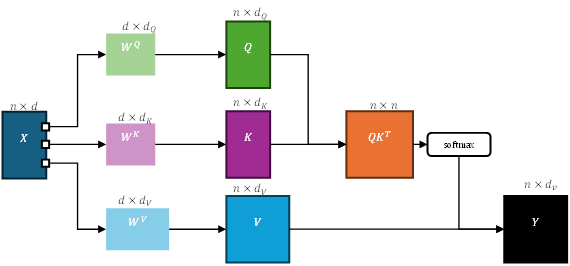
ここで $X$は入力系列、$W^Q,W^K,W^V$ はそれぞれの重み行列であり、Transformerにおける学習可能なパラメータである。この変換により、同一の入力ベクトルが「注目すべき特徴(Q)」「識別子(K)」「抽出対象(V)」という意味的に異なる空間へとマッピングされる。
この構造は、Attentionが単なる自己相似性の計算に留まらず、意味文脈に基づいた情報抽出機構として機能するための必須条件である。Q/K/Vの分離は、オブジェクト指向における「役割分担されたメソッド群の動的選択」にも通じるものであり、Self-Attentionの抽象性とOOPの構造的柔軟性との接点をより精緻に捉えるための重要な視点となる。
抽象構造としての共通点:文脈依存的自己評価
| 項目 | OOPの self | Self-Attention |
| 自己の定義 | クラス文脈に応じた振る舞い参照 | 入力系列文脈に応じた意味の再構成 |
| 動的性 | 実行時型に応じてメソッドが変わる | 各入力に応じて自己表現が変化 |
| 操作の構造 | 振る舞いの基底選択・再射影 | 意味的基底への重み付き射影 |
| 数学的解釈 | 基底変換 + 射影(型 ≒座標系の切り替え) | ソフトな基底再構成(軸のフィルタリング) |
| フィルタ的性質 | 実装継承を通じた有効な振る舞いの制限 | 重み付き注意により重要な軸を強調・抽出 |
統一的再解釈
両者の構造を線形代数の枠組みにおいて抽象化すれば、どちらも次のように捉えられる:
「自己成分を、ある文脈に基づいて再射影し、選択的に意味づけし直す操作」OOPにおける self は型空間における「射影的自己参照」、Self-Attention における self は意味空間における「動的フィルタ的自己参照」とも言える。
この対応は、オブジェクト指向とニューラルネットワークの形式構造が、いずれも「動的な基底選択と射影の枠組み」の中で記述可能であることを示唆している。両者は異なる次元で「自己を構成する空間的前提」を持っているが、その操作の核は共通している:自己は常に“他”との関係によって定義される。
例:シンプルなSelf-Attentionの実装
import numpy as np
import matplotlib.pyplot as plt
# トークン数と埋め込み次元の設定
num_tokens = 5
embedding_dim = 4
attention_dim = 4 # Attention空間の次元(通常はembedding_dimと同じか異なる)
# ランダムな埋め込みベクトルを生成(各トークンの特徴)
np.random.seed(42)
tokens = np.random.rand(num_tokens, embedding_dim)
# 重み行列の定義(線形変換:1×1 convに相当)
W_Q = np.random.rand(embedding_dim, attention_dim)
W_K = np.random.rand(embedding_dim, attention_dim)
W_V = np.random.rand(embedding_dim, attention_dim)
# Query, Key, Value の生成(線形変換)
Q = tokens @ W_Q
K = tokens @ W_K
V = tokens @ W_V
# Attentionスコアの計算(QとKの内積)
scores = Q @ K.T
# スケーリング(埋め込み次元の平方根で割る)
scaled_scores = scores / np.sqrt(attention_dim)
# softmaxによる正規化(各トークンが他トークンにどれだけ注目するか)
def softmax(x):
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True)) # 安定化
return exp_x / np.sum(exp_x, axis=-1, keepdims=True)
attention_weights = softmax(scaled_scores)
# 出力ベクトルの計算(ValueにAttention重みをかけて合成)
output_vectors = attention_weights @ V
# Attention重み行列の可視化
plt.figure(figsize=(6, 5))
plt.imshow(attention_weights, cmap='viridis')
plt.colorbar()
plt.title("Self-Attention Weight Matrix")
plt.xlabel("Attended Token Index")
plt.ylabel("Query Token Index")
plt.xticks(range(num_tokens))
plt.yticks(range(num_tokens))
plt.tight_layout()
plt.show()
# 出力ベクトルの表示(各トークンが自己参照を含めて合成した結果)
print("Output vectors (after self-attention):")
print(output_vectors)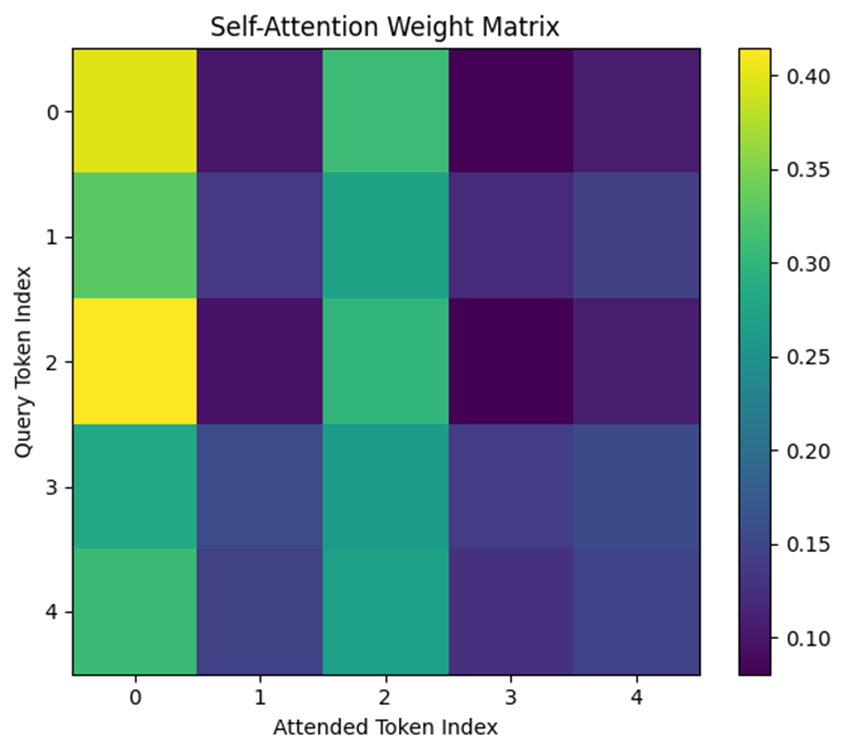
Output vectors (after self-attention):
[[0.8171592 1.00426184 0.69930635 1.31138005]
[0.7915625 0.96723906 0.66875262 1.25601252]
[0.81875423 1.00416968 0.70712603 1.31194758]
[0.77771824 0.94955796 0.64721517 1.2291082 ]
[0.7857578 0.9602772 0.65909118 1.24542999]]

コメント