Skip ConnectionとODE：変化と恒常の構造分離

その他のエッセイはこちら

はじめに

Skip Connection（スキップ結合）は、深層学習において重要な構造の一つであるとされている。ResNetをはじめとする多くのモデルで採用されており、勾配消失問題の緩和や学習の安定化に寄与すると言われている。

一般的には、Skip Connectionは「層を飛び越えて情報を伝えるショートカット」として説明されることが多い。通常、情報は層を一段ずつ順番に通って処理されていくが、Skip Connectionでは、深い層に直接情報を届けることができる。この構造により、情報の伝達がスムーズになり、より深いネットワークでも学習が安定するとされている。特に、入力に近い情報が深い層でも保持されることで、勾配消失問題の緩和に役立つとされている。

なお、本稿では構造名として「Skip Connection」という用語を用いる。これは、ResNetなどで「Residual Connection」と呼ばれることもあるが、構造的には同一であり、用語の一致性を重視して統一する。

筆者自身はこの構造の直感的な意味を十分に掴みきれていなかった。筆者は、制御理論や物理演算を主たる専門としており、AIや深層学習に関する知識はまだ不完全である。だが、だからこそ、Skip Connectionを自分の馴染みのある枠組み――たとえば常微分方程式（ODE）や数値積分――の視点から捉え直すことで、何か新しい理解が得られるのではないかと考えた。

本稿は、そのような試みの一環として書かれたものである。Skip ConnectionとODEのEuler法との構造的な類似性に着目し、両者の対応関係を数理的に整理する。特に、Skip Connectionを「変化項」と「恒常項」に分離して捉えることで、勾配の流れの安定性や勾配消失問題の緩和メカニズムを明らかにすることを目的とする。

本稿の読者としては、機械学習や深層学習の基礎を学んだ大学生・大学院生を想定しており、ニューラルネットワークの構造を数理的に再解釈することに関心を持つ層を対象とする。

本稿を読むための前提知識

本稿では、Skip ConnectionとODEの構造的対応を数理的に考察する。読者が以下のような基礎知識を持っていると、内容の理解がよりスムーズになると考えられる：

本稿における議論の範囲と限界

本稿は、Skip Connectionの構造をODEとの形式的な類似性から再解釈する試みであり、理論的な厳密性よりも構造的な直感と数理的対応関係の整理を重視している。以下の点において、議論には限界がある：

これらの点を踏まえ、本稿はあくまで「構造的な見立てによる理解の補助」として位置づけられるものである。

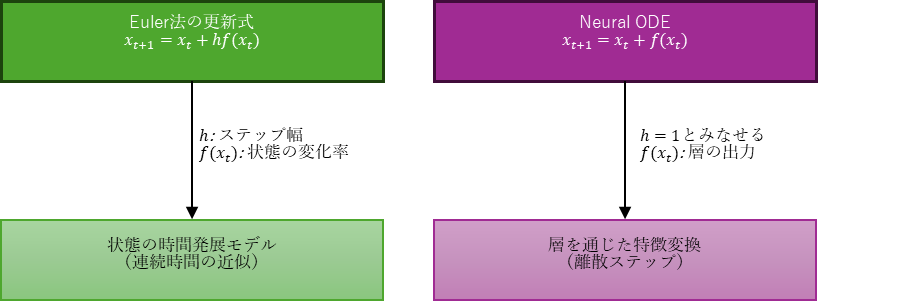
Euler法との比較：変化項と恒常項

常微分方程式（ODE）のEuler法による離散化は、以下のように表される：

ここで、$x_t$ は現在の状態、$f(x_t)$ はその変化率、$h$ はステップ幅である。深層学習におけるSkip Connectionは、これと非常に似た構造を持つ：

この式は、「現在の状態」＋「変化」という構造を持ち、ODEの時間発展と一致する。Skip Connectionは、変化を加える前の状態を保持することで、ネットワークが「何を変えるか」に集中して学習できるようにする設計思想と捉えることができる。

誤差逆伝播と連鎖律の数理的説明

本節では、ニューラルネットワークにおける誤差逆伝播法（Backpropagation）のうち各層の出力ベクトル $x^{(l)}$ に対する損失関数 $L$ の勾配がどのように伝播するかを、連鎖律（Chain Rule）に基づいて数理的に説明する。

これは、実際の重みパラメータ $W^{(l)}$ の更新に必要な勾配 $\frac{\partial L}{\partial W^{(l)}}$ を求める前段階として、誤差（勾配）がネットワーク内をどのように流れるかを理解するためのものである。

基本形（1層分）

ある層 $l$ における出力 $x^{(l)}$ に対する損失の勾配は、次のように表される：

多層構造の場合

出力層 $x^{(L)}$ から入力層 $x^{(l)}$ までの勾配伝播は、以下のように連鎖律の積として表される：

ここでの $k$ は層のインデックスであり、層 $l$ から最終層 $L$ に至るまでの各層を順にたどる。

この式から明らかなように、各層の微分（ヤコビアン）が小さいと、勾配が層を遡るにつれて指数的に減衰するため、初期層の学習が困難になる。これがいわゆる勾配消失問題の本質である。

※補足：重みパラメータ $W^{(l)}$ に対する勾配 $\frac{\partial L}{\partial W^{(l)}}$ は、ここで求めた $\frac{\partial L}{\partial x^{(l)}}$ を用いて、さらに連鎖律を適用することで計算される。

このように、逆伝播では「誤差の伝播」と「重みの勾配計算」が連携して行われる。

勾配消失のシミュレーション

以下は、sigmoid活性化関数を用いた場合に、勾配が層を通じてどのように減衰するかをシミュレーションした結果である。:

import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数とその導関数を定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    s = sigmoid(x)
    return s * (1 - s)

# 層ごとの勾配減衰をシミュレーション
num_layers = 20
x = np.ones(num_layers)  # 各層への入力を1と仮定
gradients = []

# 初期勾配（損失関数からの勾配）
grad = 1.0

for i in range(num_layers):
    # 現在の層におけるシグモイドの導関数を計算
    d = sigmoid_derivative(x[i])
    grad *= d  # 勾配を更新
    gradients.append(grad)

# 各層における勾配の大きさをプロット
plt.figure(figsize=(8, 5))
plt.plot(range(1, num_layers + 1), gradients, marker='o')
plt.title("Gradient decay across layers using sigmoid activation")
plt.xlabel("Layer")
plt.ylabel("Gradient magnitude")
plt.grid(True)
plt.tight_layout()
plt.show()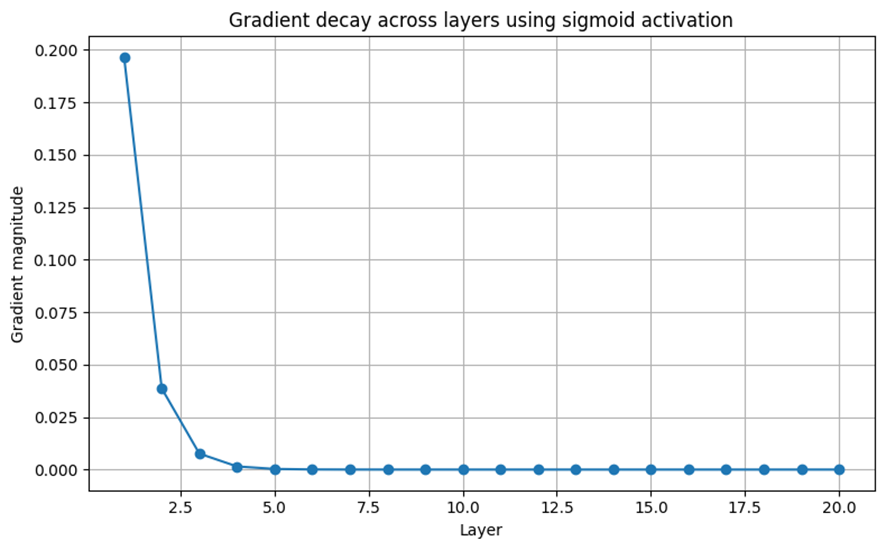

この図は、各層において勾配がどの程度減衰するかを示している。初期層では勾配が1であっても、層を重ねるごとに急速に小さくなっていくことがわかる。これは、sigmoidの導関数が最大でも0.25程度であることに起因しており、深いネットワークでは勾配がほとんど伝わらなくなる。

Skip Connectionによる緩和：構造的分離の効果

Skip Connectionを含む層では、出力が次のように表される：

このときの勾配は：

ここで $I$ は、関数としての恒等写像 $f(x) = x$ の微分であり、ヤコビ行列として単位行列となる。一方、線形代数の文脈では、単位行列は入力ベクトルを変化させずにそのまま出力する作用を持ち、恒常項として機能する。

この構造的特徴により、Skip Connectionは勾配の流れにおいて「変化項」と「恒常項」を分離する役割を果たす。特に、恒常項である単位行列 $I$ を通じて、勾配が常に1倍で伝播される経路が保証されるため、勾配が完全に消失することがなくなる。これは、深層ネットワークにおける勾配消失問題の緩和において、Skip Connectionが果たす中心的な役割である。

このように、Skip Connectionは単なるショートカット構造ではなく、数理的には「恒常項による勾配の保証」と「変化項による学習の柔軟性」を両立させる設計思想に基づいている。構造的分離によって、ネットワークは「何を変えるか」に集中して学習できると同時に、「何を保つか」によって安定性を確保しているのである。

勾配伝播の比較実験

以下は、Skip Connectionの有無によって勾配の流れがどのように変化するかを比較した実験結果である。：

活性化関数：Sigmoid
層数：12層
Skip Connection：3層ごとに残差を加算

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
import random

# 固定シードの設定（再現性の確保）
torch.manual_seed(10)
np.random.seed(10)
random.seed(10)

# Sigmoid活性化関数を使用
activation = nn.Sigmoid()

# 12層の全結合ネットワーク（Skip Connectionなし）
class DeepNet(nn.Module):
    def __init__(self):
        super(DeepNet, self).__init__()
        self.layers = nn.ModuleList([nn.Linear(10, 10) for _ in range(12)])
        self.output = nn.Linear(10, 1)

    def forward(self, x):
        for layer in self.layers:
            x = activation(layer(x))
        x = self.output(x)
        return x

# 12層の全結合ネットワーク（複数のSkip Connectionあり）
class DeepSkipNet(nn.Module):
    def __init__(self):
        super(DeepSkipNet, self).__init__()
        self.layers = nn.ModuleList([nn.Linear(10, 10) for _ in range(12)])
        self.output = nn.Linear(10, 1)

    def forward(self, x):
        residual = x
        for i, layer in enumerate(self.layers):
            x = activation(layer(x))
            if i % 3 == 2:  # 3層ごとにSkip Connectionを追加
                x = x + residual
                residual = x
        x = self.output(x)
        return x

# 勾配の比較関数
def compare_gradients():
    input_tensor = torch.ones((1, 10), requires_grad=True)
    target = torch.tensor([[1.0]])
    models = {'Without Skip Connection': DeepNet(), 'With Skip Connection': DeepSkipNet()}
    grad_results = {}

    for name, model in models.items():
        grad_dict = {}
        input_clone = input_tensor.clone().detach().requires_grad_(True)
        output = model(input_clone)
        loss = nn.MSELoss()(output, target)
        loss.backward()

        # 各層の重みの勾配ノルムを記録
        for i, layer in enumerate(model.layers):
            grad_norm = layer.weight.grad.norm().item()
            grad_dict[f'Layer {i+1}'] = grad_norm

        grad_results[name] = grad_dict

    # プロット
    plt.figure(figsize=(10, 6))
    for name, grads in grad_results.items():
        layers = list(grads.keys())
        values = list(grads.values())
        plt.plot(layers, values, marker='o', label=name)

    plt.title("Comparison of Gradient Magnitude (Sigmoid Activation, Fixed Seed)")
    plt.xlabel("Layer")
    plt.ylabel("Gradient Norm")
    plt.xticks(rotation=45)
    plt.legend()
    plt.grid(True)
    plt.tight_layout()
    plt.show()

compare_gradients()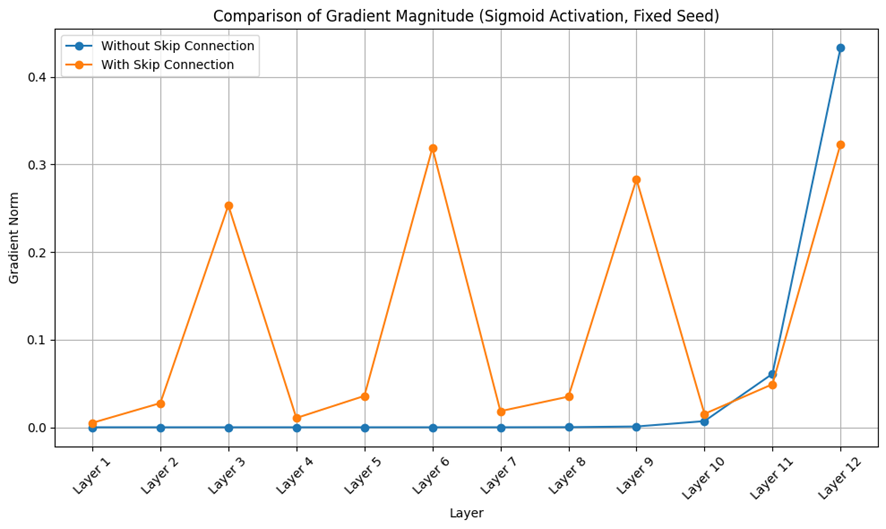

図から明らかなように、Skip Connectionを導入した場合、勾配がより均等に各層に分布している。一方、Skip Connectionなしでは、後半の層に勾配が集中し、初期層の勾配が小さくなっている。これは、Skip Connectionが恒等項を通じて勾配の流れを保証する構造であることを裏付けている。

補足：活性化関数による勾配伝播の違いとSkip Connectionの補助効果

Skip Connectionは、深層ネットワークにおける勾配消失問題の緩和に寄与する構造として知られているが、その効果は活性化関数の選択にも依存する。活性化関数は、各層における非線形性を導入する役割を果たす一方で、勾配の流れに大きな影響を与える。

活性化関数の性質と勾配の流れ

• Sigmoid関数は滑らかで連続的な関数であるが、導関数の最大値が0.25程度と小さく、深いネットワークでは勾配が急速に減衰する傾向がある。このような状況下では、Skip Connectionが恒等項を通じて勾配の流れを補完する役割を果たす。
• ReLU関数は、正の入力に対して勾配が1となるため、勾配消失が起きにくいという利点がある。ただし、負の入力では勾配が0となるため、「死んだニューロン」問題が発生する可能性がある。Skip Connectionは、このような遮断された勾配の流れを補完する構造として機能する。
• Swishは、$\text{Swish}(x)=x⋅\text{sigmoid}(x)$ と定義され、導関数が常に非ゼロで滑らかに変化するため、勾配の流れがより安定する。Skip Connectionとの併用により、勾配の均等な伝播がさらに促進されると考えられる。

実験：活性化関数とSkip Connectionの相互作用

以下のコードおよび図は、Sigmoid・ReLU・Swishの各活性化関数において、Skip Connectionの有無による勾配の流れの違いを比較したものである。各モデルは12層の全結合ネットワークで構成され、3層ごとにSkip Connectionを挿入した構造と、挿入しない構造を比較している。

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np

# 固定シードの設定（再現性の確保）
torch.manual_seed(10)
np.random.seed(10)
random.seed(10)

# 活性化関数を定義
activation_functions = {
    'Sigmoid': nn.Sigmoid(),
    'ReLU': nn.ReLU(),
    'Swish': lambda x: x * torch.sigmoid(x)
}

# 12層の全結合ネットワーク（Skip Connectionなし）
class DeepNet(nn.Module):
    def __init__(self, activation_name):
        super(DeepNet, self).__init__()
        self.activation_name = activation_name
        self.activation = activation_functions[activation_name]
        self.layers = nn.ModuleList([nn.Linear(10, 10) for _ in range(12)])
        self.output = nn.Linear(10, 1)

    def forward(self, x):
        for layer in self.layers:
            x = self.activation(layer(x)) if self.activation_name != 'Swish' else activation_functions['Swish'](layer(x))
        x = self.output(x)
        return x

# 12層の全結合ネットワーク（複数のSkip Connectionあり）
class DeepSkipNet(nn.Module):
    def __init__(self, activation_name):
        super(DeepSkipNet, self).__init__()
        self.activation_name = activation_name
        self.activation = activation_functions[activation_name]
        self.layers = nn.ModuleList([nn.Linear(10, 10) for _ in range(12)])
        self.output = nn.Linear(10, 1)

    def forward(self, x):
        residual = x
        for i, layer in enumerate(self.layers):
            x = self.activation(layer(x)) if self.activation_name != 'Swish' else activation_functions['Swish'](layer(x))
            if i % 3 == 2:  # 3層ごとにSkip Connectionを追加
                x = x + residual
                residual = x
        x = self.output(x)
        return x

# 活性化関数間の勾配を比較
def compare_gradients_all():
    input_tensor = torch.ones((1, 10), requires_grad=True)
    target = torch.tensor([[1.0]])
    results = {}

    for act_name in activation_functions.keys():
        for model_type in ['Without Skip Connection', 'With Skip Connection']:
            model = DeepNet(act_name) if model_type == 'Without Skip Connection' else DeepSkipNet(act_name)
            input_clone = input_tensor.clone().detach().requires_grad_(True)
            output = model(input_clone)
            loss = nn.MSELoss()(output, target)
            loss.backward()

            grad_norms = [layer.weight.grad.norm().item() for layer in model.layers]
            results[f'{act_name} - {model_type}'] = grad_norms

    # プロット
    plt.figure(figsize=(12, 6))
    for label, grads in results.items():
        plt.plot(range(1, len(grads)+1), grads, marker='o', label=label)

    plt.title("Gradient Magnitude Across Layers for Different Activation Functions")
    plt.xlabel("Layer")
    plt.ylabel("Gradient Norm")
    plt.legend()
    plt.grid(True)
    plt.tight_layout()
    plt.show()

compare_gradients_all()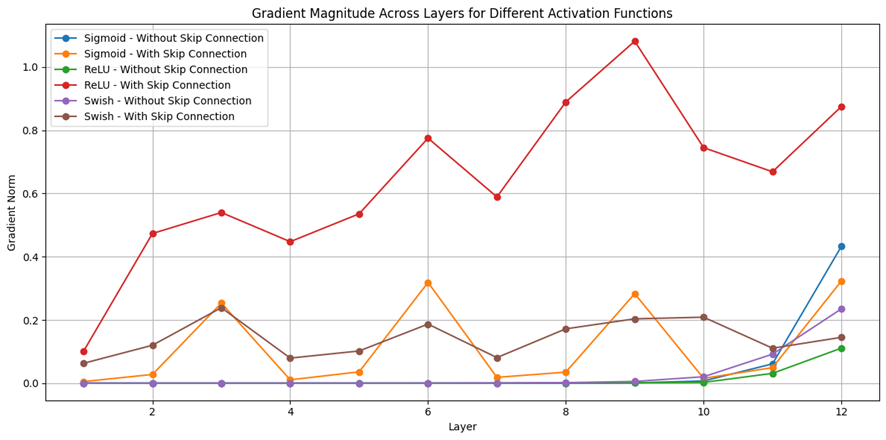

図から明らかなように、SigmoidではSkip Connectionの有無によって勾配の分布に大きな差が生じており、Skip Connectionが勾配の流れを補完する役割を果たしていることが視覚的に確認できる。ReLUやSwishにおいても、Skip Connectionを導入することで勾配の分布がより均等になり、深層ネットワークの学習が安定する傾向が見られる。

補足的まとめ：活性化関数と構造の協調

活性化関数の選択は、Skip Connectionの効果を左右する重要な要因である。Sigmoidのように勾配が減衰しやすい関数では、Skip Connectionの効果が顕著に現れる。一方、ReLUやSwishのように勾配が比較的安定している関数では、Skip Connectionは補助的な役割を果たす。したがって、Skip Connectionの構造的意義を理解するには、活性化関数との相互作用を考慮することが不可欠である。

まとめと今後の展望

本稿では、Skip Connectionの構造を常微分方程式（ODE）のEuler法との形式的な類似性から再解釈し、勾配消失問題の数理的背景とその緩和メカニズムについて考察した。Skip Connectionは、変化項と恒常項を分離することで、ネットワークが「何を変えるか」に集中して学習できる構造を提供している。また、恒等項を通じて勾配の流れを保証することで、深いネットワークにおける学習の安定性を高めている。

数式による説明に加え、Pythonによる簡易なシミュレーションを通じて、勾配の減衰とSkip Connectionの効果を視覚的に確認した。これにより、構造的な理解がより直感的に得られることを示した。

今後の展望としては、以下のような方向性が考えられる：

• Neural ODEとの比較：Skip Connectionを連続時間のモデルとして捉えた場合、Neural ODEとの関係をより厳密に整理することで、深層学習と力学系の接続がさらに明確になる可能性がある。
• 他の構造への応用：TransformerにおけるSkip ConnectionやAttention機構など、他の構造に対してもODE的な視点を適用することで、さらなる数理的理解が得られるかもしれない。
• 構造設計へのフィードバック：数理的な視点から得られた知見を、ネットワーク設計やハイパーパラメータの選定に活かすことで、より効率的なモデル構築が可能になる。

筆者自身の理解の試みとして書かれたものであるが、同様にSkip Connectionの直感が掴みきれていない読者にとって、何らかの手がかりとなれば幸いである。

補足：Neural ODEとの違いと他アーキテクチャへの接続可能性

本稿では、Skip Connectionの構造をEuler法と類比させ、ODE的な視点で再解釈した。この構造的視点は、Neural ODEやTransformerなど他の深層学習アーキテクチャとも関連しており、以下ではその接続可能性を整理する。

Neural ODEとの構造的違い

Neural ODE は、深層ネットワークを連続時間の力学系として捉えるアーキテクチャである。状態ベクトル $x(t)$ の時間発展は、次のような微分方程式で定義される：

ここで $f$ はニューラルネットワークによって定義され、$\theta$ はその学習パラメータ、$t$ は連続時間を意味する。
この式をEuler法で離散化すると、次のようなステップ更新が得られる：

この形式は、ResNetに代表されるSkip Connectionと類似している：

ただし、両者には以下の違いがある：

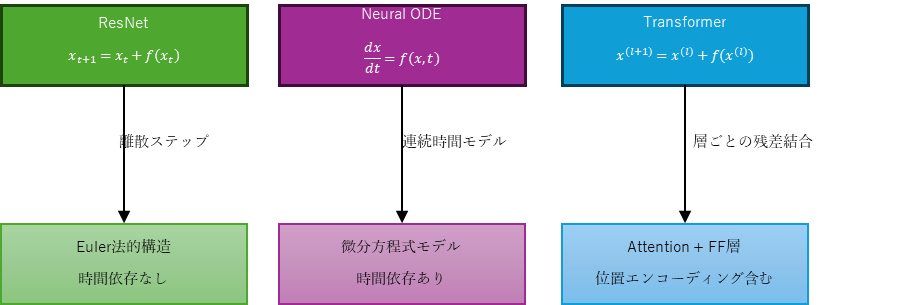
したがって、ResNet型のSkip Connectionは、Neural ODEの特殊な離散形であり、時間 $t$ を省略した静的なEuler近似とみなすことができる。

Transformerにおける残差構造とODE的理解

Transformerアーキテクチャでは、Self-Attention層やFeedforward層の出力が、入力との残差結合を通じて次層へ渡される：

この構造も、Euler法的な更新則

と同型であり、各Transformer層を「時間 $t$ における状態 $x$ の離散時間的な変化」とみなすことができる。

さらに、Transformerでは入力に位置エンコーディングが加えられるため、Attention内部の計算に時間情報 $t$ を暗黙的に供給している。これは、Neural ODEの右辺 $f(x(t), t; \theta)$ における $t$ に対応するものと解釈できる。

Attention機構と変化項の構成

Attention機構の出力は、系列全体の状態 $x$ に基づいて、各要素 $x_i$ を更新する写像である：

このとき、Attentionの出力は、ODEにおける変化項 $f(x_t)$ と解釈できる。特にSelf-Attentionは、各要素が他の要素との関係（相互作用）に基づいて変化する構造を持っており、これは非局所的なベクトル場による変化則と見なせる。

この意味で、Attentionは系列全体に依存した変化の生成器であり、単なる層内部の操作ではなく、ODEにおける「空間的に相関のある動的な変化項」としても理解可能である。

他アーキテクチャとの接続可能性

Skip ConnectionのODE的な視点は、以下のような他の構造にも拡張可能である：

統一的視座としてのODE的構造

Skip Connectionから始まり、Neural ODEやAttention、Transformerに至るまで、深層学習における多くの構造が「状態 $x$ の変化項 $f(x)$ を繰り返し適用する構造」として統一的に理解できる。この視座に立つことで、以下のような応用可能性が開ける：

このようなODE的視点は、深層学習モデルの理解を単なるブラックボックス処理から一歩進め、構造としての意味づけを可能にするものである。

参考文献

• Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. (2015). Deep Residual Learning for Image Recognition arXiv:1512.03385 [cs.CV]. https://arxiv.org/abs/1512.03385
• Srivastava, R. K., Greff, K., & Schmidhuber, J. (2015). Highway Networks. arXiv:1505.00387 [cs.LG]. https://arxiv.org/abs/1505.00387
• Dongxian Wu, Yisen Wang, Shu-Tao Xia, James Bailey, Xingjun Ma. (2020). Skip Connections Matter: On the Transferability of Adversarial Examples Generated with ResNets. arXiv:2002.05990 [cs.LG]. https://arxiv.org/abs/2002.05990

付録A：深層学習の基礎知識

ニューラルネットワークの構造

ニューラルネットワークは、複数の層を通じてデータを処理する構造を持つ。各層は、入力情報を変換し、次の層へと伝達する役割を果たす。

中間層が1つのみのネットワークは「浅いネットワーク（shallow）」と呼ばれ、複数の中間層を持つものは「深いネットワーク（deep）」と呼ばれる。

活性化関数の役割

活性化関数は、各層の出力に非線形性を導入することで、ネットワークの表現力を高める役割を担う。以下に代表的な活性化関数を示す。

関数名	数式	特徴
ReLU	$f(x)=max(0,x)$	勾配消失が起きにくく、計算効率が高い。ただし、負の入力に対して勾配が0となる「死んだニューロン」問題が発生する可能性がある。
Sigmoid	$f(x)=1/(1+e^{-x})$	出力が0〜1に収まるため、確率的解釈が可能である。一方、深いネットワークでは勾配が小さくなりやすく、勾配消失の原因となる。
Swish	$f(x)=x⋅sigmoid(x)$	滑らかで勾配が安定しやすく、近年注目されている活性化関数である。ReLUよりも性能が向上する場合がある。

活性化関数の選択は、勾配の流れや学習の安定性に大きく影響するため、モデル設計において重要な要素である。

import numpy as np
import matplotlib.pyplot as plt

# Define the activation functions
def relu(x):
    return np.maximum(0, x)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def swish(x):
    return x * sigmoid(x)

# Generate input values
x = np.linspace(-10, 10, 400)

# Compute activation values
y_relu = relu(x)
y_sigmoid = sigmoid(x)
y_swish = swish(x)

# Plot the activation functions
plt.figure(figsize=(10, 6))
plt.plot(x, y_relu, label='ReLU', color='blue')
plt.plot(x, y_sigmoid, label='Sigmoid', color='green')
plt.plot(x, y_swish, label='Swish', color='red')

# Add labels and legend
plt.title('Activation Functions: ReLU, Sigmoid, Swish')
plt.xlabel('Input')
plt.ylabel('Output')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()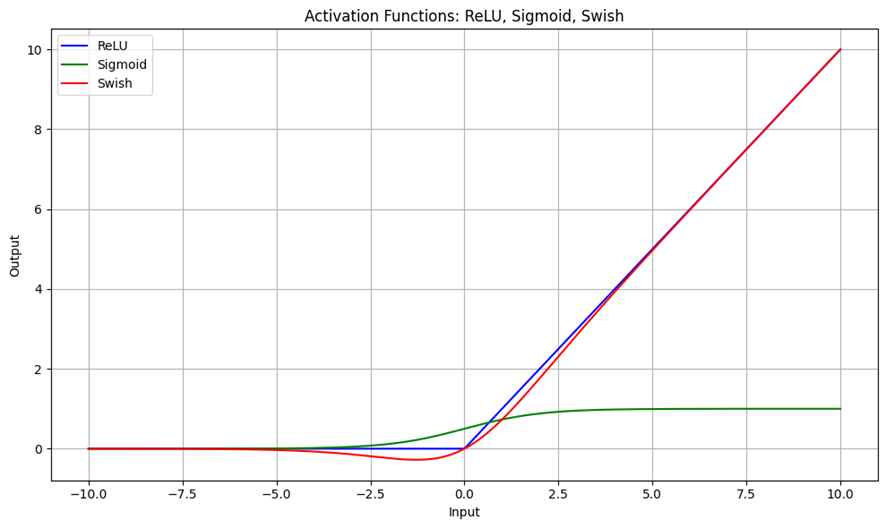

誤差逆伝播法（Backpropagation）

誤差逆伝播法は、ニューラルネットワークの学習において、損失関数 $L$ の勾配をネットワーク全体に伝播させ、各層の重みパラメータを更新するための基本的な手法である。

この手法では、連鎖律（Chain Rule）を用いて、出力層から入力層へと誤差（損失の勾配）を順に伝播させる。各層では、まず出力ベクトル $x^{(l)}$ に対する損失の勾配を計算し、それを活性化関数の導関数と掛け合わせて、線形変換前の勾配 $\frac{\partial L}{\partial z^{(l)}}$ を求める。その後、重みパラメータ $W^{(l)}$ に対する勾配を導出する。

層の構造と勾配の流れ

各層の出力は、以下のように定義される：

このとき、逆伝播では次のようなステップで勾配が計算される：

出力に対する損失の勾配（誤差の伝播）：

活性化関数の導関数を掛けて線形変換前の勾配へ：

重みパラメータに対する勾配：

多層構造における誤差の伝播（一般化）

出力層 $x^{(L)}$ から任意の層 $x^{(l)}$ までの誤差の伝播は、以下のように一般化される：

この式は、活性化関数の導関数を含めた誤差の伝播構造を表しており、勾配消失や活性化関数の選択が学習に与える影響を数理的に説明する基盤となる。

順伝播（Forward Pass）

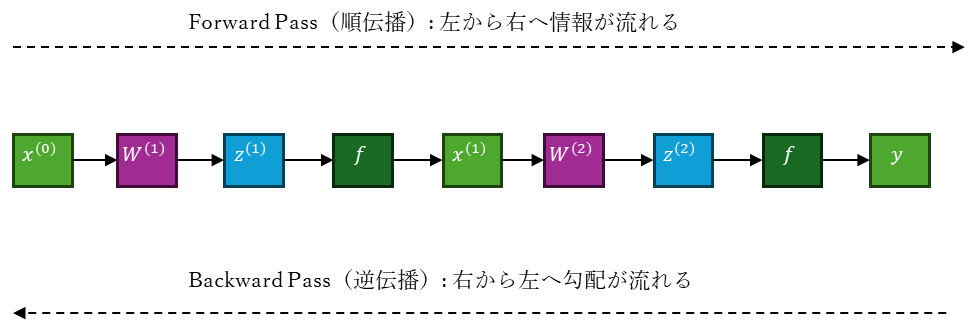
逆伝播をたどると、各層における構成要素（線形変換・活性化関数）ごとに、損失関数の勾配は以下のように計算される。：

統合的な一般式（重み更新まで含む）

層 $l$ における重み勾配は、誤差の伝播と重み依存性の両方を含めて次のように表される：

この式は、誤差逆伝播法の本質を数理的に統合したものであり、誤差の流れ・活性化関数の影響・重みの更新がどのように連携しているかを明示している。

付録B：数理的背景（ODE・線形代数）

本付録では、Skip Connectionの構造的理解に必要となる数理的背景として、常微分方程式（ODE）および線形代数の基礎事項を概説する。

常微分方程式（ODE）の基本

常微分方程式（Ordinary Differential Equation）は、ある変数の時間的変化を記述する数理モデルである。一般的な形式は以下の通りである：

ここで、$x$ は状態変数、$t$ は時間、$f$ は状態の変化率を定める関数である。ODEは、物理現象や制御系、人口動態など、時間に依存する系の記述に広く用いられる。

Euler法による数値解法

ODEの解析解が得られない場合、数値的に近似する手法が用いられる。その中でも最も基本的な手法がEuler法である。

Euler法では、時間を離散化し、次のような更新則により状態を近似する：

ここで、$h$ はステップ幅（時間の刻み）であり、$f(x_t)$ は現在の状態における変化率である。ステップ幅 $h$ を小さくすることで、連続時間の挙動をより精密に近似することが可能となる。

この更新則は、Skip Connectionの構造と形式的に類似しており、深層学習における層の更新をODE的に解釈する基盤となる。

線形代数の基礎

Skip Connectionの数理的理解には、線形代数の基本的な概念も不可欠である。以下に主要な要素を整理する。

ベクトルと行列

• ベクトル：複数の数値を並べた一次元の構造であり、状態や特徴量の表現に用いられる。
• 行列：ベクトルの変換を表す二次元構造であり、層の重みや線形写像として機能する。

単位行列と恒等写像

• 単位行列 $I$：対角成分がすべて1で、その他が0である正方行列。任意のベクトル $x$ に対して $Ix = x$ を満たす。
• 恒等写像：入力をそのまま出力する写像であり、Skip Connectionにおける「恒常項」として機能する。

単位行列と恒等写像の関係

線形代数において、恒等写像とは、任意のベクトルに対してそのままの値を返す写像である。すなわち、写像 $I$ が恒等写像であるとは、任意のベクトル $x$ に対して以下を満たすことで定義される：

この恒等写像は、行列としては単位行列（identity matrix）によって表現される。$n$ 次元空間における単位行列 $I_n$ は、対角成分がすべて1で、それ以外が0である正方行列である。例えば、3次元の場合は以下のようになる：

この行列をベクトル $x = [x_1, x_2, x_3]^T$ に作用させると、以下のようになる：

このように、単位行列は恒等写像として機能し、入力ベクトルを変化させることなくそのまま出力する。

Skip Connectionにおいては、この恒等写像が「恒常項」として機能し、勾配の流れを保証する役割を果たしている。すなわち、勾配が完全に消失することなく、少なくとも恒等項を通じて伝播される構造が確保されている。

付録C：Pythonによる数値実験の準備

本付録では、Skip Connectionの効果や勾配消失の挙動を数値的に検証するために必要となる、Python環境および基本的なライブラリの使用方法について概説する。

使用ライブラリ

数値実験には、以下の主要なライブラリを用いる。

これらのライブラリは、Python環境において標準的に使用されるものであり、深層学習の研究や実験において不可欠である。

基本的なコード構成

数値実験を行う際のコードは、以下のような構成を持つ。

再現性の確保

数値実験においては、結果の再現性を確保することが重要である。乱数の初期化により、毎回同じ結果が得られるように設定する。

import torch
import numpy as np
import random

torch.manual_seed(10)
np.random.seed(10)
random.seed(10)

このように、各ライブラリに対して乱数シードを固定することで、実験結果の一貫性が保たれる。

実験の目的と位置づけ

本稿における数値実験は、理論的な構造理解を補助するためのものであり、実運用モデルの性能評価を目的とするものではない。簡易なネットワーク構成と固定された入力に基づき、Skip Connectionの有無による勾配の流れの違いや、活性化関数の選択による影響を視覚的に確認することを主眼としている。

その他のエッセイはこちら