MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その65【単純パーセプトロンで分類①】
MATLAB,Python,Scilab,Julia比較 第4章 その66【単純パーセプトロンで分類②】
MATLAB,Python,Scilab,Julia比較 第4章 その67【単純パーセプトロンで分類③】
を書き直したもの。
単純パーセプトロンで分類を行う。
逆伝播の復習を行いつつ、分類の方法を考える。
逆伝播の復習と最適化とプログラム化についての話がメイン。
単純パーセプトロンの構造
前回までで、逆伝播の話が終わった。
のだが、
重みに着目しただけだから、
実際の逆伝播はもう少し複雑になる。
以前も説明したと思うが、
単純パーセプトロンの本来の活性化関数はヘヴィサイド関数。
構造としては以下のようになる。
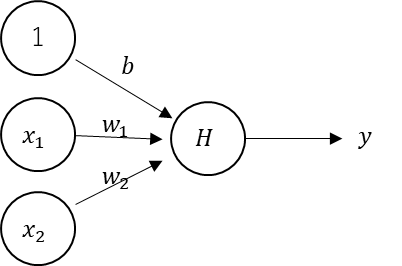
しかし、活性化関数がヘヴィサイド関数だと、勾配が無いから逆伝播が効かない。
そこで、活性化関数をシグモイド関数に差し替えたものを
今回の単純パーセプトロンとしている。
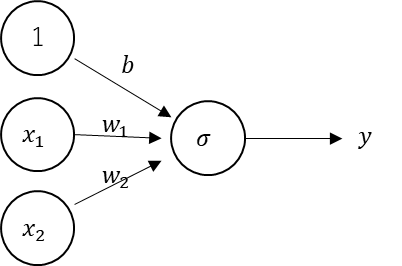
これで逆伝播が効くようになる。
本来の単純パーセプトロンは逆伝播による学習はしないが、
逆伝播の最もシンプルな挙動をみるには単純パーセプトロンくらいシンプルな構造な方が見やすいので、
無理やり採用してる感じ。
逆伝播は本来だと誤差逆伝播法が正式名称だけど、
単純パーセプトロンに使用される用語ではないところから、
意図的に「逆伝播」って言い方にしている。
逆伝播の復習
逆伝播の復習をしておこう。
重みの逆伝播
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial W}&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial W}\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X
\end{eqnarray}
\)
バイアスの逆伝播
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial b}&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial b}\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot 1\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}
\end{eqnarray}
\)
こうしてみると、重みとバイアスの逆伝播って途中まで一緒なことがわかると思う。
つまり、プログラム化する際に表現の最適化が可能。
最適化
というわけで最適化する。
実際のところは、数式上で共通部分があるから、その演算を共通化するだけ。
重みとバイアスの連鎖律に於いて、
以下の赤字の部分が共通となっている。
重みの逆伝播
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial W}&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial W}\\
&=&{\color{red}(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}}\cdot X
\end{eqnarray}
\)
バイアスの逆伝播
\(
\begin{eqnarray}
\displaystyle\frac{\partial E}{\partial b}&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial b}\\
&=&(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot 1\\
&=&{\color{red}(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}}
\end{eqnarray}
\)
というわけで、まずは赤字の部分を算出してしまう。
この部分を\(dZ\)とする。
\(
\begin{eqnarray}
\displaystyle dZ&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}=(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X\\
&=&
\Bigg(
\begin{bmatrix}
a_1\\a_2\\a_3\\a_4
\end{bmatrix}-
\begin{bmatrix}
0\\0\\0\\1
\end{bmatrix}
\Bigg)\circ
\sigma\Bigg(
\begin{bmatrix}
z_1\\z_2\\z_3\\z_4
\end{bmatrix}
\Bigg\{
1-\sigma\Bigg(
\begin{bmatrix}
z_1\\z_2\\z_3\\z_4
\end{bmatrix}
\Bigg)
\Bigg\}
\end{eqnarray}
\)
そして、重みへの連鎖律は以下に最適化される。
\(
\displaystyle\frac{\partial E}{\partial W}=dZ^TX=
\begin{bmatrix}
dz_1\\dz_2\\dz_3\\dz_4
\end{bmatrix}^T
\begin{bmatrix}
0&0\\
0&1\\
1&0\\
1&1\\
\end{bmatrix}
\)
バイアスの連鎖律は以下
\(
\displaystyle\frac{\partial E}{\partial b}=\sum dZ=
\begin{bmatrix}
dz_1\\dz_2\\dz_3\\dz_4
\end{bmatrix}^T
\begin{bmatrix}
1\\1\\1\\1
\end{bmatrix}
\)
プログラムで実現する場合は、途中の変数に結果を格納できるから、
その部分で処理の最適化ができるってことになる。
次のページへ
次のページから実際にプログラムに向けてのフローとか、学習過程に於ける決定境界線の動き方を確認する。





コメント