関数をハックせよ：多項式回帰・フーリエ級数・ニューラルネットによる関数近似戦略

その他のエッセイはこちら

筆者の立ち位置と本稿の目的

筆者は自動車業界でエンジニアとして働いており、日々の業務ではセンサーデータや物理モデルの解析に携わっている。特に、多項式回帰やフーリエ変換を用いた関数近似や信号処理は、実務で頻繁に活用している技術である。

一方で、関数近似よりも数値微分・数値積分といった数値近似の方が実装も簡単で、現場では扱いやすいと感じることも多い。しかし、導関数や原始関数が明確な既知の関数で近似できることの応用性の高さも強く意識しており、関数近似の価値を再認識する機会が増えている。

本稿では、そうした実務的な視点から、関数近似の代表的な手法である多項式回帰・フーリエ級数・ニューラルネットワークを比較し、それぞれの「ハックの仕方」と応用可能性について考察する。理論と実装の間にあるギャップを埋め、現場で使える知識としての関数近似を再評価することを目的としている。

想定読者

このエッセイは、以下のような読者を想定している：

データ分析やモデリングに関心のあるITエンジニア・技術者
実務で多項式回帰やフーリエ変換を使ったことがあるが、ニューラルネットワークとの違いを整理したい人
数値近似は得意だが、関数近似の理論的な意味や応用性を深掘りしたい人
数式に抵抗はないが、実装や応用に直結する視点を求めている人

データの裏に潜む「関数」を見抜け

現代のITエンジニアが扱うデータは、単なる数字の羅列ではない。センサーからの時系列データ、ユーザーの行動ログ、音声波形、画像のピクセル値——それらはすべて、何らかの関数的な構造を持っている。だが、その関数が明示的に与えられることはほとんどない。むしろ、関数は「隠れている」ものだ。

この隠れた関数を見抜き、モデル化する技術が「関数近似」である。関数近似とは、既知のデータや関数項をもとに、未知の関数の形を推定するアプローチであり、統計解析、信号処理、機械学習など、あらゆる分野で活用されている。

多項式回帰——古典的だが侮れない

数学的背景

多項式回帰は、線形回帰の拡張として登場した手法で、データの非線形性を捉えるために高次の項を追加する。基本的な形は以下の通り：

$$
y=a_0 + a_1 x + a_2 x^2 + \dots +a_n x^n
$$

この式の係数 $a_i$ を最小二乗法などで求めることで、データにフィットする曲線を得る。次数を上げることで複雑な形状にも対応できるが、過学習のリスクが高まる。

プロトタイピング：簡単に実装できるため、初期のモデル構築に向いている。
解釈性の高さ：係数の意味が明確で、モデルの挙動を説明しやすい。
制約条件のある場面：物理モデルや経済モデルなど、理論的に多項式が妥当な場合。

注意点

高次の多項式は振動しやすく、外挿に弱い。
データのスケーリングが重要。特に高次項では数値的に不安定になることがある。

フーリエ級数——周期性をハックする

数学的背景

フーリエ級数は、周期関数を三角関数の線形結合で表現する手法。基本形は以下の通り：

$$
f(x)\simeq a_0+\sum_{n=1}^\infty[a_n\cos(n\omega x)+b_n\sin(n\omega x)]
$$

この式の係数（フーリエ係数）を求めることで、元の関数の形を再構成できる。周波数領域での解析が可能になるため、信号処理や音声認識、画像圧縮などで広く使われている。

実務での使いどころ

周期的なデータ：センサーの振動データ、季節性のある売上データなど。
ノイズ除去：高周波成分をフィルタリングすることで、スムーズな信号を得られる。
スペクトル解析：音声や画像の特徴抽出に活用。

注意点

非周期的なデータには不向き。
ギブズ現象（急激な変化点での振動）に注意。
離散フーリエ変換（DFT）や高速フーリエ変換（FFT）との違いを理解する必要あり。

ニューラルネットワーク——汎用近似器の登場

数学的背景

ニューラルネットワークは、活性化関数と重みの組み合わせによって、任意の関数を近似する。特に多層パーセプトロン（MLP）は、ユニバーサル近似定理により、任意の連続関数を近似可能とされている。

$$
y=\sigma(W_3\cdot(W_2\cdot\sigma(W_1\cdot x+b_1)+b_2)+b_3)
$$

ここで $\sigma$ は活性化関数（ReLU, Sigmoid, Tanhなど）、$W_i$ は重み行列、$b_i$ はバイアス項。

ユニバーサル近似定理とは？

ユニバーサル近似定理とは、「1つの隠れ層を持つ前向きニューラルネットワークは、十分なユニット数があれば、任意の連続関数を任意の精度で近似できる」という理論である（Cybenko, 1989／Hornik, 1991 などによる）。これは、ニューラルネットが「汎用近似器」と呼ばれる所以でもある。

ただし、これは存在を保証する定理であり、実際にその関数を学習できるかどうかは、ネットワークの構造や学習アルゴリズム、データの質に大きく依存する。つまり、「理論的にはできるが、実務では工夫が必要」というのが現実である。

実務での使いどころ

複雑な非線形関係：画像認識、自然言語処理、異常検知など。
大量のデータ：データ量が多いほど性能が向上しやすい。
自動特徴抽出：手動で特徴量を設計する必要がない。

注意点

解釈性が低い：ブラックボックス的で、なぜその出力になるかが分かりにくい。
学習コストが高い：計算資源と時間が必要。
過学習・過適合：正則化やドロップアウトなどの工夫が必要。

実践編：3手法の関数近似をコードで比較してみよう

理論だけではピンとこない方のために、ここでは実際に Python を使って、3つの関数近似手法を比較してみる。対象はノイズ付きの正弦波。これを多項式回帰、フーリエ級数、ニューラルネットワークで近似し、それぞれの挙動を可視化する。

データ生成：

正弦波にランダムノイズを加えた合成データを生成。
近似対象となる「真の関数」として扱う。

多項式回帰:

5次の多項式でデータを近似。
scikit-learn を使って、特徴量変換と回帰モデルの学習を行う。
出力は滑らかな曲線だが、端部で振動しやすい傾向がある。

フーリエ級数近似（FFT + 共役対称性保持）:

scipy.fft を使って周波数成分を抽出。
先頭5成分（DC成分 + 4周波数）を保持し、対応する複素共役を末尾に再構成。
ifft によって逆変換し、実数信号として近似波形を得る。
周期性のある滑らかな近似が得られる。

ニューラルネットワークによる近似:

PyTorch を使って、2層の全結合ニューラルネットワークを構築。
活性化関数には Tanh を使用し、非線形性を表現。
1000エポック学習し、ノイズを含む関数形状を柔軟に近似。

可視化:

各手法の近似結果を並べて表示。
元のノイズ付きデータと比較することで、近似の精度や特徴を視覚的に把握できる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, ifft
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import torch
import torch.nn as nn

# 合成データの生成
np.random.seed(0)
x = np.linspace(0, 2 * np.pi, 100)
y_true = np.sin(x) + 0.2 * np.random.randn(100)  # noisy sine wave

# --- 多項回帰 ---
poly = PolynomialFeatures(degree=5)
X_poly = poly.fit_transform(x.reshape(-1, 1))
model_poly = LinearRegression()
model_poly.fit(X_poly, y_true)
y_poly_pred = model_poly.predict(X_poly)

# --- フーリエ級数近似法 ---
# Use FFT to approximate the signal
y_fft = fft(y_true)
y_fft_filtered = np.zeros_like(y_fft)
y_fft_filtered[:5] = y_fft[:5]
y_fft_filtered[-4:] = np.conj(y_fft[1:5][::-1])  # 実数信号を得るために共役対称性を再構成
y_fourier_pred = np.real(ifft(y_fft_filtered))

# --- ニューラルネットワーク近似法 ---
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(1, 64),
            nn.Tanh(),
            nn.Linear(64, 64),
            nn.Tanh(),
            nn.Linear(64, 1)
        )

    def forward(self, x):
        return self.net(x)

# Prepare data for PyTorch
x_tensor = torch.tensor(x, dtype=torch.float32).view(-1, 1)
y_tensor = torch.tensor(y_true, dtype=torch.float32).view(-1, 1)

# モデルの初期化とトレーニング
model_nn = SimpleNN()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model_nn.parameters(), lr=0.01)

for epoch in range(1000):
    optimizer.zero_grad()
    output = model_nn(x_tensor)
    loss = criterion(output, y_tensor)
    loss.backward()
    optimizer.step()

y_nn_pred = model_nn(x_tensor).detach().numpy().flatten()

# --- 可視化 ---
plt.figure(figsize=(15, 10))

plt.subplot(2, 2, 1)
plt.plot(x, y_true, label='True Data', color='gray')
plt.title('Original Noisy Sine Wave')
plt.legend()

plt.subplot(2, 2, 2)
plt.plot(x, y_true, label='True Data', color='gray')
plt.plot(x, y_poly_pred, label='Polynomial Regression', color='blue')
plt.title('Polynomial Regression Approximation')
plt.legend()

plt.subplot(2, 2, 3)
plt.plot(x, y_true, label='True Data', color='gray')
plt.plot(x, y_fourier_pred, label='Fourier Approximation (5 Components)', color='green')
plt.title('Fourier Series Approximation')
plt.legend()

plt.subplot(2, 2, 4)
plt.plot(x, y_true, label='True Data', color='gray')
plt.plot(x, y_nn_pred, label='Neural Network Approximation', color='red')
plt.title('Neural Network Approximation')
plt.legend()

plt.tight_layout()
plt.show()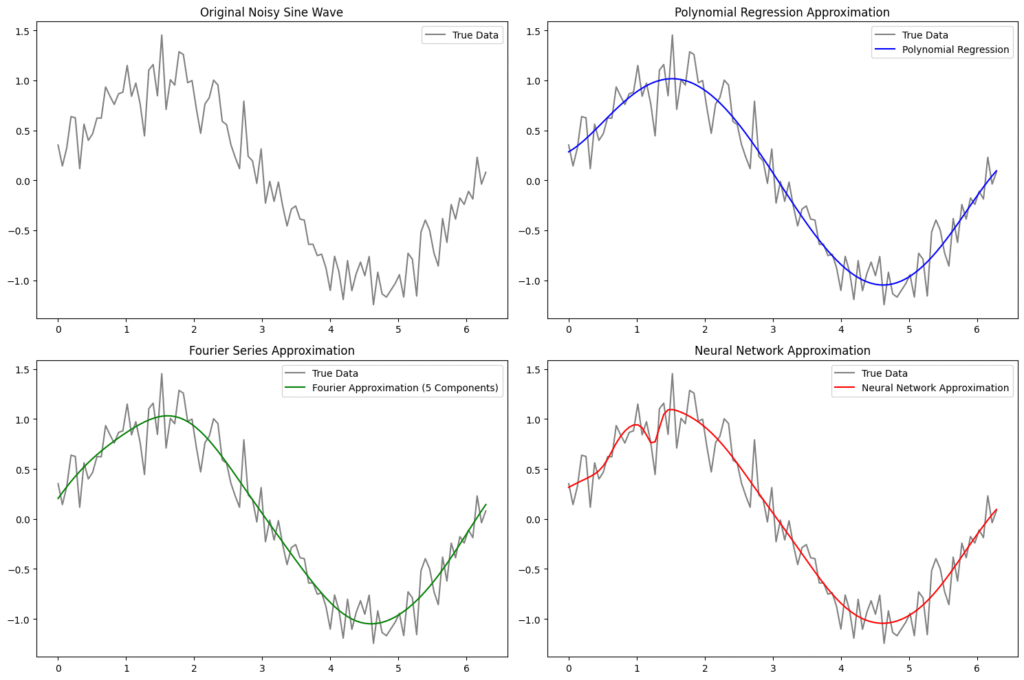

この図からも分かるように、各手法には得意・不得意がある。次章では、それらの違いと共通点を整理し、どのように使い分けるべきかを考察する

ニューラルネットワークの構造とハイパーパラメータ選定の背景

今回のネットワーク構成は、2層の全結合ネットワークで、各層に64ユニットを持ち、活性化関数には Tanh を使用している。Tanh は滑らかな S 字カーブを描くため、正弦波のような連続的な非線形関数の近似に適している。ReLU では角ばった近似になりやすく、今回のような滑らかな波形には不向きな場合がある。

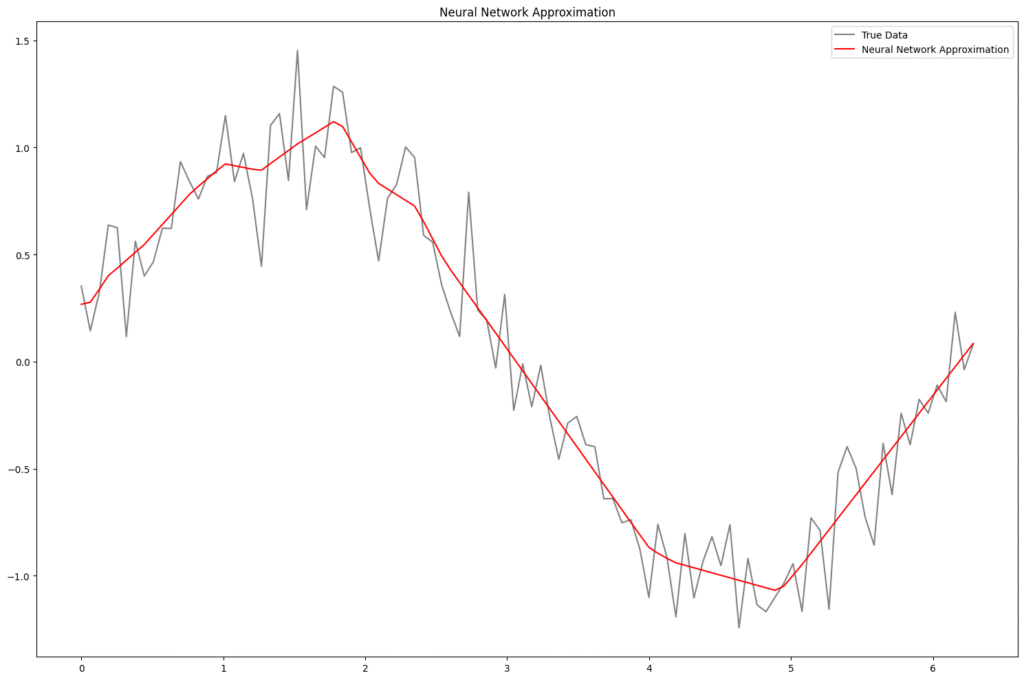
構造の意図

層の深さ：ユニバーサル近似定理により、1層でも任意の連続関数を近似可能とされるが、2層にすることで学習の安定性と収束速度が向上する傾向がある。
ユニット数（64）：過学習を避けつつ、十分な表現力を確保するためのバランス設計。より複雑な関数や高次元データに対しては、ユニット数の増加や層の追加が必要になる。
活性化関数（Tanh）：正弦波のような滑らかな関数を近似する際に、Tanh の連続性と対称性が有利に働く。ReLU では近似が角ばる傾向があり、今回のような連続関数には不向きな場合がある。

ハイパーパラメータの選定

パラメータ設定値選定理由

パラメータ	設定値	選定理由
学習率（lr）	0.01	Adam 最適化において安定した初期値。収束速度と精度のバランスを考慮。
エポック数	1000	ノイズを含む関数を十分に近似するための学習回数。過学習の兆候が見られた場合は早期終了も検討可能。
最適化手法	Adam	勾配のスケーリングとモーメンタムを自動調整するため、収束が速く、実務でも広く使われている。
損失関数	MSE（平均二乗誤差）	回帰問題において最も一般的で、誤差の大きさを定量的に評価できる。

このような構成とパラメータ設定は、関数近似のベースラインとしては十分に機能する。実務では、データの性質や目的に応じて、層の深さやユニット数、活性化関数、正則化手法（Dropout, L2など）を柔軟に調整する必要がある。

共通点と違い——ハックの哲学

これら3つの手法は、いずれも「既知の関数項を組み合わせて未知の関数を近似する」という共通の哲学を持っている。違いは、使う関数項の種類（多項式、三角関数、活性化関数）と、近似の方法（解析的、周波数的、学習的）にある。

しかし、単に理論を知っているだけでは十分ではない。それぞれの手法には「使いこなしの勘所」があり、そこを押さえることで、より効果的な近似が可能になる。

多項式回帰のハック:

次数を上げすぎないことが肝心。高次の多項式は過学習や振動の原因になるため、交差検証や情報量規準（AIC, BICなど）を使って適切な次数を選ぶのがポイント。
- AIC（赤池情報量規準）は、モデルの複雑さとデータへの適合度のバランスを評価する指標で、値が小さいほど望ましい。
- BIC（ベイズ情報量規準）は、AICに比べてモデルの複雑さに対してより厳しいペナルティを課すため、データ数が多い場合により保守的なモデル選択ができる。
スケーリングの工夫も重要。高次項が数値的に不安定になるのを防ぐため、入力データの標準化や正規化を行うとよい。

フーリエ級数のハック: