数理的なエッセイ集｜数理OSで世界認識をアップデートする「破壊系シリーズ」

その他数理関連(MATLAB、Python、Scilab、Julia比較ページ)はこちら

【入門】MATLAB,Python,Scilab,Julia使い方比較【数値計算プログラム】

MATLAB,Python,Scilab,Juliaを比較。基本的な計算、ベクトル行列演算、グラフ(波形)表示、伝達関数、画像取り込み、最小二乗法を元に比較しています。それぞれツールの特性が理解できれば使い分けも移行も難しくは無いでしょう。似ている部分も多いので私の場合はそれを利用するして実験の幅を広げています。

はじめに
エッセイ集

はじめに

なんとなく思いつきで書いたエッセイ集。
「普通はこうだよね？」「みんなこうだよね？」を別の視点でぶん殴ってみる実験エッセイ

適当なタイミングで更新

エッセイ集

ソフトウェア設計における因果関係の明確化
条件分岐や状態遷移の数理的な記述
並列処理やバッチ処理の自然な導入
AIモデルとの構造的な共通性の理解

オブジェクト指向を線形代数で読み解く:エンジニアのための思考実験

ソフトウェア設計における因果関係の明確化。条件分岐や状態遷移の数理的な記述。並列処理やバッチ処理の自然な導入。 AIモデルとの構造的な共通性の理解。

多項式回帰のハック
フーリエ級数のハック
ニューラルネットのハック

関数をハックせよ：多項式回帰・フーリエ級数・ニューラルネットによる関数近似戦略

その他のエッセイはこちら筆者の立ち位置と本稿の目的筆者は自動車業界でエンジニアとして働いており、日々の業務ではセンサーデータや物理モデルの解析に携わっている。特に、多項式回帰やフーリエ変換を用いた関数近似や信号処理は、実務で頻繁に活用してい...

「箱」は、プログラミング教育において非常に強力なメタファーである。だが、箱に閉じ込められたままでは、複雑な構造や動的な関係性を見失ってしまう。クラス、オブジェクト、関数、変数——それぞれの概念は、箱として捉えることもできるが、それ以上の意味と構造を持っている。

「全部箱かい！！！」——プログラミング概念に潜む“箱”のメタファーの功罪とその深層

ロジカルシンキングによって導かれる結果は、現実においては一つの仮説に過ぎない。しかし、その過程と表現には大きな価値がある。誤りを構造的に認識し、他者と共有し、柔軟に修正していくための基盤として、ロジカルシンキングは不可欠な思考技術である。

ロジックは現実に負けるのか？──エンジニアが語る論理的思考の再評価

ロジカルシンキングによって導かれる結果は、現実においては一つの仮説に過ぎない。しかし、その過程と表現には大きな価値がある。誤りを構造的に認識し、他者と共有し、柔軟に修正していくための基盤として、ロジカルシンキングは不可欠な思考技術である。現実の複雑さを前提にしながらも、論理という道具を使って前に進むこと。それこそが、現代における思考の成熟であると私は考える。

技術開発の現場において、ロジカルシンキングは強力な武器である。しかし、それが現実という複雑な集合の一部に過ぎないことを理解し、その思考構造を柔軟に「再構成」できる能力こそが、不確実な未来を切り拓くための重要な鍵となるだろう。

論理思考の限界と再構築──集合論・群論で読み解く技術開発の構造

その他のエッセイはこちら※本稿では集合論や群論といった数学的概念を思考の補助線として扱っている。集合論に馴染みのない読者のために、文末に「付録：集合論の基本と導入のための問い」を設けた。「集合とは何か」「写像とは何か」といった基礎を簡潔に確...

Attentionは、技術と知能の本質をつなぐ架け橋であり、AIが人間の認知に近づくための重要なステップである。そして、自動車技術においても、より安全で賢い車両知能の実現に向けた鍵となる。

CNNとFCの融合体：Attention機構が切り開く知能の地形図

その他のエッセイはこちら序論：抽象化のジレンマとAttentionの登場本稿は、自動車業界に従事するエンジニアの視点から、AI技術の中でも特に注目されているAttention機構について、その構造的・機能的意義を探るものである。筆者自身はA...

Neural ODEとの比較：Skip Connectionを連続時間のモデルとして捉えた場合、Neural ODEとの関係をより厳密に整理することで、深層学習と力学系の接続がさらに明確になる可能性がある。
他の構造への応用：TransformerにおけるSkip ConnectionやAttention機構など、他の構造に対してもODE的な視点を適用することで、さらなる数理的理解が得られるかもしれない。
構造設計へのフィードバック：数理的な視点から得られた知見を、ネットワーク設計やハイパーパラメータの選定に活かすことで、より効率的なモデル構築が可能になる。

Skip ConnectionとODE：変化と恒常の構造分離

Neural ODEとの比較：Skip Connectionを連続時間のモデルとして捉えた場合、Neural ODEとの関係をより厳密に整理することで、深層学習と力学系の接続がさらに明確になる可能性がある。他の構造への応用：TransformerにおけるSkip ConnectionやAttention機構など、他の構造に対してもODE的な視点を適用することで、さらなる数理的理解が得られるかもしれない。構造設計へのフィードバック：数理的な視点から得られた知見を、ネットワーク設計やハイパーパラメータの選定に活かすことで、より効率的なモデル構築が可能になる。

損切りは本能的には不快で、「続けていれば良い結果が出たかもしれない」という未練も残りがちだが、
「損切り＝負け」ではなく「損切り＝未来のための資源再配分」と捉え直すと、投資・研究開発・プロジェクト・キャリアなどで共通の判断軸として使える。
ここで書いたのは筆者の一例にすぎないので、共感できる部分だけ拾って自分の文脈に合わせてカスタマイズし、最終判断は自分自身の責任で行ってほしい。

損切りは“損”じゃない？投資から研究開発まで使える意思決定の型

損切りは本能的には不快で、「続けていれば良い結果が出たかもしれない」という未練も残りがちだが、「損切り＝負け」ではなく「損切り＝未来のための資源再配分」と捉え直すと、投資・研究開発・プロジェクト・キャリアなどで共通の判断軸として使える。ここで書いたのは筆者の一例にすぎないので、共感できる部分だけ拾って自分の文脈に合わせてカスタマイズし、最終判断は自分自身の責任で行ってほしい。

メディアを「フィルター」として見る
“静かな良コンテンツ”を自分で集めておく
数字は人気指標としてだけ使う

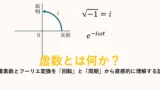
【考察】テレビ・SEO・インフルエンサーはなぜ“似た構造”に見えるのか【情報のゲーム】

テレビ・SEO・インフルエンサーなどのオールド／ニューメディアがなぜ“似た構造”に見えるのかを、広告モデルやアルゴリズム、視聴率・クリック率といった数字のゲームから整理し、受け手としての距離の取り方を考える考察記事。

虚数・複素数は「√-1という謎の数」ではなく、回転と周期・位相を扱うために数直線を2次元に拡張した座標。
sin, cos とオイラーの公式で三角関数を複素平面に閉じ込めることで、微分積分が「iω を掛ける」という代数的な操作に変わる。
フーリエ変換とラプラス変換はどちらも、信号や微分方程式を「回転（＋減衰）」の足し合わせとして見直し、面倒な微分を単なる掛け算にしてくれる道具。

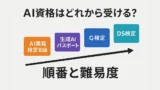
虚数とは何か？複素数とフーリエ変換を「回転」と「周期」から直感的に理解する話

虚数・複素数とフーリエ変換とは何かを「回転」と「周期」から直感的に解説。sin, cosやオイラーの公式、フーリエ変換とラプラス変換の関係まで、微分積分とのつながりをやさしく紐づけます。

「B級 → 生成AI → G検定」は難易度順として妥当
しかし難易度 = 最適ルートではない
学習は
- 基礎の広さ
- 特化の深さ
- コスト
- 目的
  に応じて設計すべき
生成AIパスポートは
「生成AI×リスク×法務×情報管理」の領域を深掘りできるため、シラバス内でもG検定より難しい問題を構築可能

AI資格はどれから受ける？生成AIパスポート・G検定・AI実装検定B級・DS検定の順番と難易度を徹底比較

生成AIパスポート・G検定・AI実装検定B級・DS検定はどの順番で受けるべきかを整理。難易度だけでなく学習の筋やサンプル問題を通して、生成AIパスポートの位置づけとG検定との違いを解説します。

AI要約とゼロクリック検索の広がりで、「基礎情報をメインにした資格記事」の役割は、入口から補足・文脈提供へとシフトしつつある。
ロジスティック関数を使った簡易モデルからは、Geminiのカバー率がある閾値を超えたあたりで、クリック率が一気に落ちる“ゲームチェンジポイント”が示唆される。
これからは、公式・一次情報と一次経験、そして資格をどう位置づけるかという視点・モデルを提示できるコンテンツの比重を高めることが重要になる。

AI時代に「資格ブログ」とSEOはどう変わるのか――ゼロクリック検索とGeminiで変わるゲームの話

AIやGeminiによるゼロクリック検索が広がる中で、「試験概要を整理した資格記事」はどんな役割に変わっていくのか。ゼロクリック率のシンプルな数式とPythonシミュレーションを使って、SEOの価値を否定せずに、これから求められるコンテンツと実務での一歩目を考えます。

暗記偏重は「生徒の怠惰」ではなく、報酬設計の結果として合理的に起きている現象だと、強化学習の視点から説明する。
強化学習では「暗記＋類題演習＝greedyな行動」「本質理解や探究＝探索的な行動」とみなせる。
個人としては、毎日10〜20分の“探索時間”（ε-greedy） を混ぜることで、テストの点数と長期的な本質理解を両立できる。

日本の「詰め込み教育」は本当に悪か？──高校教育をAIの強化学習メタファーと報酬設計の視点から読み解く

日本の高校教育はなぜ「詰め込み」「暗記偏重」と言われるのか。本記事では、AIの強化学習（greedy方策・ε-greedy・UCB）と報酬設計の視点から、日本の教育構造と暗記教育のメリット・課題、そして高校生・教師・AI好きの読者が今日から実践できる現実的な改善のヒントを整理する。

九九のような基礎暗記は、計算のためだけでなく「思考レイテンシを下げるOS」として残しておく価値がある
セレンディピティの確率を少しでも上げるには、「まず自分で考える」「雑な知識を頭に撒いておく」といった非効率が効いてくる
AIは計算や情報整理の強力なツールだからこそ、「どこまで任せてどこから自分で考えるか」を自分でデザインすることが大事

AI時代に暗記は不要？九九・フェルミ推定・セレンディピティから考える、本当に残すべき「頭の中の知識」

AI時代だから暗記は不要？──そうした“合理的な結論”の裏で失われかねないのが、セレンディピティ（思いがけない幸運な発見）と直感的な思考力です。九九やフェルミ推定を例に、人間にとっての「わざと残す非効率」の意味を、少し数理的に考えます。

「みんながなんとなく共有しているミーム」を
一度連続関数にして眺めると、
「レバー」や「形の変化」として語り直せる部分も見えてくる

「完全に理解した」を数式にして遊ぶ ── ダニング＝クルーガー効果・ハイプサイクル・生成AIの話

ネットの「完全に理解した／何もわからない／チョットデキル」ミームを、ダニング＝クルーガー効果とハイプサイクルになぞらえて、ロジスティック関数＋山と谷の「おもちゃモデル」で数式化してみるエッセイです。生成AI時代の自己評価バイアスとのつながりも軽く眺めます。

「G検定はどこから勉強を始めると挫折しにくいか」
「2024のシラバス改訂で“今寄り”になったところはどこか」
「生成AI時代に合わせた、現実的な G検定勉強法（2026年版） はどんな形か」

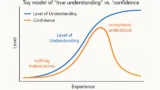
【2026年版】生成AI時代のG検定勉強法・2024シラバス攻略── 時間軸と自分事軸、それから小さな「崖」の話

ChatGPTは触っているけれどG検定テキスト第1章で挫折した人へ。G検定シラバス改訂 2024 に対応した2025年、2026年向けのG検定勉強法として、「G検定どこから勉強するか？」に答えるシラバス攻略エッセイです。生成AI時代のG検定勉強法のコツと、おすすめの読み順サンプル・30日ミニプランを解説します。

難化に見える正体は“ズレ”
ズレは5軸で測れる
対策は較正→観察→耐性

G検定が毎回「難化した！」と言われる理由：作問スタイルのズレを5軸で分解し、コサイン類似度のおもちゃモデルで理解する

G検定で毎回「難化した！」と言われる理由を、作問スタイルのズレとして5軸で分解。シラバス→公式例題→ズレ耐性の最短対策も解説。

MCPはLLM向けツール群を標準プロトコルで公開する「配線」、RESTは人間／固定ロジック向けWeb API、LangChainはアプリ内ロジック。
MCPのツール定義はそのままLLMに読ませるプロンプトなので、ツール名・引数名・descriptionの設計がクリティカル。
LangChainでのツール／エージェント設計の感覚を起点にMCPを考えると、「MCP＝ただのREST API」的なハマりどころを避けやすい。

MCPとREST API・LangChainの違いは？「ただのREST」と見るとハマる理由をLLM視点で解説

MCPとREST API・LangChainの違いと共通点をLLM視点で整理し、「ツール定義＝プロンプト」という設計の勘所を解説します。

比較は「性能」ではなく 期待値（用途×効用）で決まる
体感差は 根拠/概略/提案のデフォルトで説明できるかもしれない
重要なのは「どっちが上」より どこで逆転するか

ChatGPTとGeminiの違いは「性能差」より“検索・根拠・提案”の初期設定：体感 → 仮説 → パラメータ分解 → おもちゃモデル

ChatGPTとGeminiの体感差（個人の推測）を先に具体化し、その体感を「根拠・概略・提案・リスク」に分解。期待値の式で整理したうえで、Pythonのおもちゃモデルで用途により優位が逆転する構造を可視化します。

VLMは画像もテキストも最終的には「トークン列」として扱い、Self-Attentionでトークン同士の関係（どこをどれだけ見るか）を学習している。
Attentionマップは「この概念は画像のどの領域に対応していそうか」という暗黙の“領域分け”情報を持つが、ピクセル精度のセグメンテーションの完全な代替ではない。
マルチスケール特徴は、CNN＋FPNでもViT系でも「解像度の異なる特徴から何個のトークンを作るか」という設計の違いであり、実務ではVLMのAttentionと専用セグメンテーション（SAMなど）を組み合わせて使うのが現実的。