バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は、余弦定理の証明。
任意の三角形を2つの直角三角形にすることで各辺を三角関数して表現可能。
これに加えて、三角比の基本公式を加えると、余弦定理が求まる。
今回は、この余弦定理を使って、内積をベクトル成分に用いて算出できることを証明する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
内積の定義【再掲】

次は内積の定義と余弦定理の組み合わせで。
ベクトルの成分表記の内積がどのように成立するか求める。

日本語でしゃべって欲しいんだけど・・・。

(純度100%の日本語だよ・・・。)

まずは、内積の定義を再掲する。
内積の定義
\(|\vec{a}||b|\cos(\theta)\)
内積の定義と余弦定理から成分表記の内積を求める

なす角\(\theta\)となる\(\vec{a}\)と\(\vec{b}\)を元に以下の図を考える
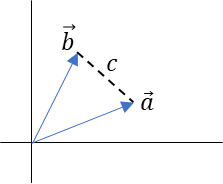

この場合、3辺の長さは以下となる。
\(a=|\vec{a}|\)
\(b=|\vec{b}|\)
\(c=|\vec{b}-\vec{a}|\)

ここに余弦定理を適用すると以下になる。
\(|\vec{a}|^2+|\vec{b}|^2+2|\vec{a}||\vec{b}|\cos(\theta)=|\vec{b}-\vec{a}|\)

上記を変形して、内積の定義と合わせると、
\(|\vec{a}||\vec{b}|\cos(\theta)=\displaystyle\frac{1}{2}(|\vec{a}|^2+|\vec{b}|^2-|\vec{b}-\vec{a}|)\)

そして、右辺を計算していくが、
\(\vec{a}\)の成分は\((a_1,a_2)\)
\(\vec{b}\)の成分は\((b_1,b_2)\)
とする。
\(\displaystyle\frac{1}{2}(|\vec{a}|^2+|\vec{b}|^2-|\vec{b}-\vec{a}|)\)
\(=\displaystyle\frac{1}{2}\{a_1^2+a_2^2+b_1^2+b_2^2-(a_1-b_1)^2-(a_2-b_2)^2\}\)
\(=\displaystyle\frac{1}{2}(2a_1 b_1+2a_2 b_2)\)
\(=a_1 b_1+a_2 b_2\)

つまり、以下が成立する。
\(|\vec{a}||\vec{b}|\cos(\theta)=a_1 b_1+a_2 b_2\)

おー!
それぞれの内積の形は見たことあったけど、
余弦定理を経て同一だと証明されていたのか!

そして、この式の右辺側の成分表記の内積が方程式と強い関係性があるってことだな。

(またよくわからんこと言い出した。)
まとめ

まとめだよ。
- 内積の定義と余弦定理から成分表記の内積を求めた。
- ベクトルとしての内積と、成分表記としての内積が等しいことを証明。
- 上記を利用して、内積が方程式と強い関係性があることを示すの次回。
バックナンバーはこちら。




コメント