G検定が毎回「難化した！」と言われる理由：作問スタイルのズレを5軸で分解し、コサイン類似度のおもちゃモデルで理解する

Q: G検定は公式の過去問が公開されていますか？

JDLA公式に「例題・過去問」ページがあり、一部の過去出題が掲載されています。https://www.jdla.org/certificate/general/issues/

Q: シラバス改訂はどこで確認できますか？

JDLAの告知ページと、シラバス配布ページで確認できます。https://www.jdla.org/news/20240514001/ https://www.jdla.org/download-category/syllabus/

Q: コサイン類似度を使う意味は何ですか？

コサイン類似度は、大きさ（知識量）より向き（スタイル配分）の違いに敏感だからです。作問スタイルの回転を直感的に扱えます。https://itlab.uta.edu/courses/CSE5334-data-mining/current-offering/module-clustering/cosine-similarity-tutorial.pdf

その他のエッセイはこちら

※G検定の試験概要・具体的な勉強ステップ・無料700問問題集は、

合わせて読むことおすすめ記事
要約（先に3行）
G検定が毎回「難化した！」と言われる理由は“難易度”ではなく“ズレ”にある
公式「例題・過去問」はあるが、回ごとの“全量セット”で較正しにくい
仮説：難化体感の正体は「作問スタイルの向き」がズレたこと
作問スタイルのズレを5軸で分解する（G検定の作問傾向を言語化）
1. 1）分野配分（Topic allocation）
2. 2）認知レベル（Cognitive demand）
3. 3）形式（Question format）
4. 4）新しさ（Update / recency）
5. 5）ひねり・曖昧さ（Trickiness / ambiguity）
問題集が寄せがちなポイント（ズレに気づくための観点）
公式例題で較正する：5軸チェックシート（テンプレ付き）
1. 最短手順
2. 0/1/2 採点テンプレ（コピペ用）
おもちゃモデル：コサイン類似度で“向きのズレ”を可視化する
1. 5軸を“配分ベクトル”として扱う
2. コサイン類似度で“スタイルの近さ”を測る
3. 「難化した！」は閾値を跨ぐと増える（ロジスティック）
図とコードは何を示している？（横軸・縦軸の読み方）
シミュレーション（Python）：ズレが増えると「難化した！」確率が上がる
G検定の勉強法：シラバスで較正→公式例題で観察→ズレ耐性を作る
まとめ：G検定の「難化した！」は“作問スタイルのズレ”で説明できる
1. まとめのまとめ（3行）
FAQ
1. Q1. G検定は公式の過去問が公開されていますか？
2. Q2. なぜG検定は毎回「難化した！」と言われやすいのですか？
3. Q3. シラバス改訂はどこで確認できますか？
4. Q4. コサイン類似度を使う意味は何ですか？
5. Q5. 閾値 τ や鋭さ α はどう決めればいいですか？
参考文献（個人ブログ・一般企業ブログ・書籍は除外／URL併記）
G検定の“較正”に使う（公式・シラバス準拠）
機械学習の“見取り図”を作る（認知レベルを上げる）
ディープラーニングを“なぜそうなるか”で理解する（初見耐性）
数学・統計（コサイン類似度／ロジスティックの土台）
類似度・情報検索（“コサイン類似度の使いどころ”を固める）
法務・倫理（G検定で“ズレやすい周辺・横断”を埋める）
学習法（「難化した！」の体感＝メタ認知・テスト効果を攻略）

合わせて読むことおすすめ記事

【2026年版】生成AI時代のG検定勉強法・2024シラバス攻略── 時間軸と自分事軸、それから小さな「崖」の話

ChatGPTは触っているけれどG検定テキスト第1章で挫折した人へ。G検定シラバス改訂 2024 に対応した2025年、2026年向けのG検定勉強法として、「G検定どこから勉強するか？」に答えるシラバス攻略エッセイです。生成AI時代のG検定勉強法のコツと、おすすめの読み順サンプル・30日ミニプランを解説します。

要約（先に3行）

「難化した！」は、難易度の上昇というより作問スタイルの“向き”がズレた体感として起きやすい
ズレは「分野配分・認知レベル・形式・新しさ・ひねり」の5軸で分解できる
対策は シラバスで較正 → 公式例題で型を観察 → ズレ耐性を作る が最短ルートになりやすい

G検定が毎回「難化した！」と言われる理由は“難易度”ではなく“ズレ”にある

G検定は、受験回ごとに「今回、難化した！」という声が出やすい試験です。もちろん本当に難しくなった可能性もあります。
ただ、SNSや受験後の振り返りで目立つのは、客観難度の上昇という断定というより、“問われ方の向き”が想定とズレたときの初見感（知らない感じ）が「難化した！」へ変換される現象です。

この記事では、難度を断定するのではなく、受験者の体感として何が起きているかを再利用できる枠組み（5軸）で整理します。後半では、その枠組みをコサイン類似度＋ロジスティックの“おもちゃモデル”で眺めます。

公式「例題・過去問」はあるが、回ごとの“全量セット”で較正しにくい

JDLA公式には「例題・過去問」ページがあり、一部の過去出題が掲載されています。
https://www.jdla.org/certificate/general/issues/

一方で、学習者が「回（年度）単位の問題セットを丸ごと使って作問スタイルを把握する」前提の設計とは限りません（ページ上は、トピック別に個別問題が並ぶ形式として扱いやすい構成です）。

比較として、IPAの過去問題は年度別に「問題冊子・解答例・採点講評」などへ辿れる導線が用意されています。
https://www.ipa.go.jp/shiken/mondai-kaiotu/index.html

この違いは、体感としてこう効きます。

年次セットが揃いやすい：学習者側の「出題像」が収束しやすい（ズレが小さくなりやすい）
断片サンプル中心になりやすい：教材ごとに想定が分岐しやすく、ズレが“別方向”へ回転しやすい（体感が荒れやすい）

この記事の主題は、まさにこの「ズレが回転する」側です。

仮説：難化体感の正体は「作問スタイルの向き」がズレたこと

仮説はシンプルです。

本試験の作問スタイルと、問題集（予想問題）が暗黙に持つ作問スタイルが近いほど「見たことある」
逆に向きがズレるほど「知らない」「解きにくい」
この「知らない感じ」が、主観的には「難化した！」として表れやすい

この“近さ”を精神論ではなく、5軸のベクトルとして定義し、後半でコサイン類似度（向きの近さ）で眺めます。

作問スタイルのズレを5軸で分解する（G検定の作問傾向を言語化）

ここでのポイントは、「難しかった／簡単だった」を言い合うのではなく、ズレた軸を特定して対策を寄せることです。

1）分野配分（Topic allocation）

シラバス全体の中でどこに重みを置くか。最新版は公式から確認できます。
https://www.jdla.org/download-category/syllabus/

例：頻出領域が薄くなり、別領域が厚くなる
例：「広く浅く」→「特定領域だけ妙に深い」

2）認知レベル（Cognitive demand）

用語の想起だけか、理解・適用・判断まで問うか。

例：定義 → ケースに当てはめて判断
例：暗記 → 例外条件つきで選択

3）形式（Question format）

問題の出し方そのもの。形式が変わると「知ってるのに解けない」が起きます。

例：短文確認 → 長文から条件を拾う
例：素直な選択肢 → 近い概念が密集した選択肢で区別させる

4）新しさ（Update / recency）

改訂・新しめの話題をどれだけ混ぜるか。
（例：シラバス改訂の告知）
https://www.jdla.org/news/20240514001/

5）ひねり・曖昧さ（Trickiness / ambiguity）

素直に解ける問いが多いのか、境界条件・曖昧語・例外が勝負になるのか。

例：素直な正誤 → 「どちらとも言える」を排除する力が必要
例：典型 → 例外・境界条件で揺さぶる

問題集が寄せがちなポイント（ズレに気づくための観点）

問題集が悪い、という話ではありません。問題集は「学習を進めやすくする」ために、どうしても設計上の寄せ（バイアス）が入ります。
ただ、その寄せ方が本試験の作問スタイルと違う方向へ大きいと、「難化した！」体感が起きやすくなります。

分野配分：定番に寄りやすく、横断・周辺が薄くなりがち
認知レベル：暗記・想起中心になりやすく、条件つき判断が弱くなりがち
形式：短文・素直形式に寄りやすく、長文・複数条件・紛らわしさに弱くなりがち
新しさ：更新サイクル差で改訂点の反映が遅れやすい
ひねり：学習者満足のため“素直”に寄りやすく、境界条件への耐性が育ちにくい

公式例題で較正する：5軸チェックシート（テンプレ付き）

素材：
https://www.jdla.org/certificate/general/issues/

最短手順

公式例題から10～20問選ぶ
自分の教材から同数（10～20問）選ぶ
各問に「5軸×0/1/2」を付ける
軸ごとの平均（または割合）を比べて、どの軸がズレているかを見る
ズレが大きい軸にだけ対策を寄せる（全部やらない）

0/1/2 採点テンプレ（コピペ用）

分野配分：0=頻出ど真ん中 / 1=準頻出・周辺 / 2=薄い・横断が強い
認知レベル：0=用語想起 / 1=理解・比較 / 2=適用・判断（条件つき）
形式：0=短文素直 / 1=長文・条件複数 / 2=選択肢が紛らわしい・複合
新しさ：0=古典・定番 / 1=近年の整理 / 2=改訂・新潮流が強い
ひねり：0=素直 / 1=境界条件 / 2=曖昧語・例外が勝負

おもちゃモデル：コサイン類似度で“向きのズレ”を可視化する

ここからは「整理を数式の形に落として眺める」パートです。厳密な実証モデルではなく、どの仮定が効いて、どこで体感が跳ねるかを可視化するための道具です。

コサイン類似度の入門（PDF）
https://itlab.uta.edu/courses/CSE5334-data-mining/current-offering/module-clustering/cosine-similarity-tutorial.pdf

5軸を“配分ベクトル”として扱う

5軸の強さを、合計1になる配分（確率分布）として表します。

基準（本試験側の想定）：$a = softmax(z^{(A)})$
ズレ後（教材側の想定）：$v(g) = softmax(z(g))$

ズレ量を $g \in [0,1]$ とし、軸ごとのズレやすさを $c_i$ とします。

遷移係数：$\lambda_i(g) = exp(-c_i g)$
ロジット混合：$z_i(g) = \lambda_i(g) z^{(A)}_i + (1-\lambda_i(g)) z^{(B)}_i$

コサイン類似度で“スタイルの近さ”を測る

$S(g) = \dfrac{a \cdot v(g)}{|a| |v(g)|}$

$S$ が1に近い：向きが近い（スタイルが似ている）
$S$ が小さい：向きが違う（スタイルがズレている）

「難化した！」は閾値を跨ぐと増える（ロジスティック）

「難化した！」が出る確率を、類似度がある閾値 $\tau$ を下回ると増える形で置きます。

$p(g) = \sigma(\alpha(\tau – S(g)))$
$\sigma(x) = \dfrac{1}{1+exp(-x)}$

ロジスティック回帰の導入資料
https://cs229.stanford.edu/notes2022fall/main_notes.pdf
https://ocw.mit.edu/courses/15-071-the-analytics-edge-spring-2017/pages/logistic-regression/

図とコードは何を示している？（横軸・縦軸の読み方）

ここで示すPythonコードとグラフは、本試験の作問スタイルと教材の作問スタイルがズレるほど、“難化した！”と言い出す確率が上がるという仮説を、超単純化したおもちゃモデルで可視化したものです。
「本当に難しくなったか（客観難度）」を証明する目的ではなく、“問われ方の向き（スタイル）が合っていたか”が体感に効くことを直感的に理解するための図です。

横軸（Alignment gap）：$g$。0=一致、1=大きく乖離。難易度ではなくスタイルのズレ量
縦軸（P(complaint: “Harder!”))：$p(g)$。「難化した！」が出る確率のイメージ

また2本の線は、較正できている場合／できていない場合の対比です。

Aligned prep (calibrated)：公式例題などで較正できていて、教材の想定が本試験から大きく外れにくい
Biased prep (uncalibrated)：教材の想定が偏っていて、ズレたときの初見感が強く出やすい

シミュレーション（Python）：ズレが増えると「難化した！」確率が上がる

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def softmax(x):
    x = x - x.max(axis=1, keepdims=True)
    e = np.exp(x)
    return e / e.sum(axis=1, keepdims=True)

gap = np.linspace(0, 1, 400)  # 0=aligned, 1=diverged

def cosine(a, v):
    num = v @ a
    den = np.linalg.norm(v, axis=1) * np.linalg.norm(a)
    return num / den

def style_vector_softmax(z_a, z_b, c):
    lam = np.exp(-np.outer(gap, c))      # (len(gap), 5)
    z = z_a * lam + z_b * (1 - lam)      # (len(gap), 5)
    return softmax(z)

# Baseline exam-writer style in logit space (near-uniform distribution)
z_a = np.array([0.0, 0.0, 0.0, 0.0, 0.0])

# Calibrated prep: small rotation
z_b_with = z_a + np.array([0.2, -0.1, 0.0, 0.0, -0.1])

# Uncalibrated prep: larger rotation (example bias on "format" and "recency")
z_b_no = np.array([-1.0, -1.0, 2.0, 0.5, 0.0])

# Drift speeds (how fast it rotates)
c_with = np.array([0.6, 0.7, 0.8, 0.5, 0.9])
c_no   = np.array([1.2, 1.4, 1.6, 1.0, 1.8])

a = softmax(z_a.reshape(1, -1))[0]
v_with = style_vector_softmax(z_a, z_b_with, c_with)
v_no   = style_vector_softmax(z_a, z_b_no,   c_no)

S_with = cosine(a, v_with)
S_no   = cosine(a, v_no)

alpha = 60.0
tau   = 0.70  # toy threshold

p_with = sigmoid(alpha * (tau - S_with))
p_no   = sigmoid(alpha * (tau - S_no))

plt.plot(gap, p_with, label="Aligned prep (calibrated)")
plt.plot(gap, p_no,   label="Biased prep (uncalibrated)")
plt.xlabel("Alignment gap (0=aligned, 1=diverged)")
plt.ylabel('P(complaint: "Harder!")')
plt.ylim(-0.02, 1.02)
plt.legend()
plt.show()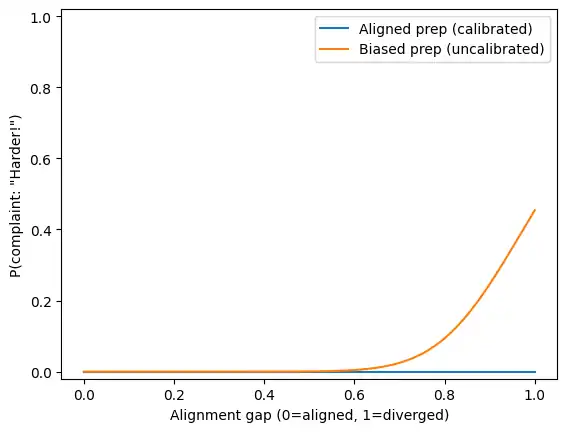

横軸はAlignment gap（0=一致、1=乖離）、縦軸は「難化した！」と言う確率。較正ありは緩やかに上昇し、較正なしはより早く高確率に達する2本の曲線。 — 作問スタイルのズレ（Alignment gap）が大きいほど、「難化した！」と感じる確率が上がる（おもちゃモデル）。較正あり／なしで曲線が変わる。

G検定の勉強法：シラバスで較正→公式例題で観察→ズレ耐性を作る

シラバスで較正：最新版シラバスで分野配分の抜けを埋める
https://www.jdla.org/download-category/syllabus/
公式例題で型を見る：解けた/解けないより、形式・認知レベル・ひねりの型を観察する
https://www.jdla.org/certificate/general/issues/
ズレ耐性の小ワーク：「定義→1文説明→ミニ適用→境界条件1つ」まで上げる

まとめ：G検定の「難化した！」は“作問スタイルのズレ”で説明できる

「難化した！」は、難度上昇の断定というより作問スタイルの向きのズレとして起きやすい
ズレは 5軸（分野配分・認知レベル・形式・新しさ・ひねり）で分解できる
対策は 較正（シラバス）→観察（公式例題）→耐性（小ワーク）が効きやすい

まとめのまとめ（3行）

難化に見える正体は“ズレ”
ズレは5軸で測れる
対策は較正→観察→耐性

FAQ

Q1. G検定は公式の過去問が公開されていますか？

JDLA公式に「例題・過去問」ページがあり、一部の過去出題が掲載されています。
https://www.jdla.org/certificate/general/issues/

Q2. なぜG検定は毎回「難化した！」と言われやすいのですか？

難度上昇そのものより、教材が作る想定と本試験の作問スタイルがズレたときに初見感が増え、それが「難化した！」として表出しやすいからです。ズレは5軸で言語化できます。

Q3. シラバス改訂はどこで確認できますか？

JDLAの告知ページと、シラバス配布ページで確認できます。
https://www.jdla.org/news/20240514001/
https://www.jdla.org/download-category/syllabus/

Q4. コサイン類似度を使う意味は何ですか？

コサイン類似度は、大きさ（知識量）より向き（スタイル配分）の違いに敏感だからです。作問スタイルの“回転”を直感的に扱えます。
https://itlab.uta.edu/courses/CSE5334-data-mining/current-offering/module-clustering/cosine-similarity-tutorial.pdf