G検定×実務の最短ブリッジで学ぶニューラルネット入門エッセンシャル（決定境界・活性化・logits損失・最適化）

Q: softmax二重がけは何がまずいですか

loss内部でlog-softmax（logsumexpによる安定化）を取る前提が崩れ、勾配が痩せたり学習が遅くなったりします。TensorFlowにもsoftmax済みを渡すと不正確になる趣旨の注意があります。https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits

要約（3行）
合わせて読むことおすすめの記事
想定シラバス
この記事を読んだ後に解けるようになる典型設問
1. 例題1
2. 例題2
試験コアだけ読むルート
G検定×実務の最短ブリッジ
注意
用語整理（logitsとlogitの混同防止）
出力層×損失の対応表
予測したい確率の形（多クラス vs マルチラベル）
パーセプトロン→ロジスティック回帰→ニューラルネットワーク
決定境界
活性化関数
1. 活性化関数の形（補足: グラフ）
交差エントロピーとlogの意味
同型で理解する数値安定化（BCEWithLogits と softmax交差エントロピー）
1. 二値分類（BCEWithLogitsの形）
2. 多クラス分類（softmax交差エントロピーの形）
数値安定性の実害（expオーバーフロー→NaN）
試験の罠（現場事故にも直結）
1. softmax二重がけ
2. BCEの入力取り違え
3. マルチラベルの取り違え
逆伝播と計算グラフ
不均衡データの実務チェックリスト（学習信号と運用判断を分ける）
1. 学習信号（モデルが学ぶ方向）
2. 運用判断（評価指標と閾値）
最適化アルゴリズム（特徴で覚える）
1. 最適化の挙動イメージ（補足: グラフ）
TensorFlow/Kerasでの同じ事故防止（フレームワーク横断の補強）
FAQ
1. logitsとlogit（log-odds）は何が違いますか
2. softmax二重がけは何がまずいですか
3. CrossEntropyLossはsoftmax済みの確率を入れるものですか
4. マルチラベルと多クラスはどう見分けますか
5. AdamWのweight decayはL2正則化と同じですか
参考文献
まとめ
合わせて読むことおすすめの記事
まず全体像を1冊でつなぐ（G検定→実務ブリッジの地図）
NumPy感覚で「腹落ち」させる（逆伝播・損失・最適化の芯）
BCE/CEを確率として締める（ロジスティック回帰・交差エントロピーの背景）
最適化を「関係性」で整理する（SGD→Momentum→Adam/AdamWの見取り図を強化）
実務フレームワークへ橋をかける（“logitsを入れる” 事故を防ぐ）
不均衡データ・評価・運用を“別レイヤー”で固める（pos_weight と閾値を混線させない）
読み順のおすすめ（最短ルート）

要約（3行）

G検定のニューラルネット頻出要点を、決定境界→活性化→交差エントロピー→逆伝播→最適化の1本線で整理します。
二値分類（BCEWithLogits）と多クラス分類（softmax交差エントロピー）は、どちらもlogsumexpに収束する同型の安定化です。
試験の罠と現場事故（softmax二重がけ、BCEの入力取り違え、不均衡の評価設計）を一緒に潰します。

合わせて読むことおすすめの記事

G検定まとめ記事

本記事の詳細版

※ 近日公開

本記事は以下のシリーズ記事の統合再編版且つエッセンシャル版です。
ゆるーい雰囲気でゆっくり読みたい人は以下のシリーズ記事の方がおすすめです。

上記シリーズ記事の統合版シリーズが含まれています。
上記がゆるすぎる場合は、以下シリーズの方が読み易いかもしれません。
(このシリーズ記事から読む方がおすすめです。)

シリーズ記事側はPythonだけでなく、MATLAB,Scilab,Juliaも使用。

想定シラバス

このページは、JDLAのG検定シラバス「G2024#6～」を想定しています。
https://www.jdla.org/news/20240514001/
https://www.jdla.org/download-category/syllabus/

この記事を読んだ後に解けるようになる典型設問

単層モデルの決定境界が直線（超平面）になる理由を説明する問題
シグモイドとReLUの特徴（長所・短所）を問う問題（飽和、勾配消失の入口）
交差エントロピーのlogが「自信満々の誤り」を強く罰する理由を述べる問題
二値と多クラスで、出力層と損失の組み合わせを選ばせる問題（BCE系 vs softmax交差エントロピー）
SGD/モーメンタム/Adam/AdamWの違いを特徴で問う問題

G検定の設問で難しく感じやすいのは、ニューラルネットや画像処理の文脈で機械学習の基本を問うパターンです。
ニューラルネットや画像処理の章では「二値・マルチラベル・多クラス」がまとまって説明されないこともありますが、考え方（原理）は共通です。
そのため実際の設問では、ニューラルネットの基礎と機械学習の基礎を同時に問われる形になり、見た目の難易度が上がります。

例題1

ある画像分類モデルを学習したい。1枚の画像には「犬」「猫」「車」など複数の物体が同時に写り得るため、1枚あたり正解ラベルは複数個になり得る（0個もあり得る）。このとき、出力層と損失関数の組み合わせとして最も適切なものはどれか。

A. 出力層は softmax、損失は交差エントロピー（多クラス）
B. 出力層は sigmoid、損失は二値交差エントロピー（各ラベル独立）
C. 出力層は softmax、損失は平均二乗誤差（MSE）
D. 出力層は恒等（活性化なし）、損失は交差エントロピー（多クラス）で、各ラベルを独立に扱う

正解はB。

■ 簡単な解説

複数ラベルが同時に正解になり得るので、各ラベルを独立な二値分類として扱い、sigmoid + BCE 系が基本です。

■ 正解の理由

softmax は確率の合計が1になるため「必ず1つだけ正解（相互排他）」の多クラス分類向きです。
今回は「犬も猫もあり得る」ため相互排他ではなく、各ラベルを独立にON/OFF判定する必要があります。
そのため、各ラベルごとに確率を出す sigmoid と、各ラベル独立の二値交差エントロピー（BCE）が適切です。

■ 不正解の理由

A：softmax は「どれか1つ」を前提にするため、複数同時正解に不向きです。
C：分類問題で MSE を使うと学習がうまく進みにくいことが多く、標準的ではありません。
D：交差エントロピー（多クラス）は相互排他前提なので「各ラベル独立」と矛盾します。

■ まとめ

複数ラベル同時に正解になり得るなら、基本は「sigmoid + BCE（各ラベル独立）」です。

例題2

あるタスクでニューラルネットを学習している。以下の条件を満たす設定として最も適切な組み合わせはどれか。

1サンプルに対して正解ラベルは複数あり得る（0個もあり得る）
ラベル数は多く、各ラベルは独立にON/OFF判定したい
学習は比較的小さめのバッチで行う
L2正則化（weight decay）を入れたいが、Adam系の挙動として「勾配へのL2加算」と「weight decay」を混同したくない（安定に効かせたい）

A. 出力：softmax、損失：多クラス交差エントロピー、最適化：SGD
B. 出力：sigmoid、損失：二値交差エントロピー、最適化：Adam
C. 出力：sigmoid、損失：BCEWithLogits（logits版BCE）、最適化：AdamW
D. 出力：softmax、損失：平均二乗誤差（MSE）、最適化：AdamW

■ 正解

■ 簡単な解説

マルチラベル分類は「各ラベルを独立にON/OFF判定する」問題なので、基本は sigmoid＋BCE 系（実務では logits 版の BCEWithLogits）になります。
また AdamW は weight decay（重みを直接縮める処理）を勾配計算と切り離すため、Adam に L2 を足す形と混同しにくいのがポイントです。
なお AdamW はG検定シラバスで明示されないこともありますが、weight decay の説明や比較の文脈で言及されやすい背景があります。
出題範囲の解釈には温度差があり得ますが、weight decay を問う設問で AdamW に触れられる可能性はゼロではありません。試験対策としては「Adam と AdamW の違いを1行で説明できる」程度まで押さえておくのが安全側です。

■ 正解の理由

複数ラベルが同時に正解になり得るので、各ラベルを独立な二値分類として扱います。
→ 出力は sigmoid（確率）に相当し、損失は各ラベル独立の二値交差エントロピーが適切です。
実務では数値安定性のため、確率ではなく logits をそのまま損失に渡す「BCEWithLogits（sigmoid込み）」がよく使われます。
さらに AdamW は weight decay（重みを直接縮める）を勾配処理から分離するため、Adamで起きやすい「L2を勾配に足す形（$\lambda w$）と同じつもりで使って挙動がズレる」混乱を避けやすいです。

■ 不正解の理由

A：softmax＋多クラス交差エントロピーは「正解は必ず1つ」の相互排他が前提で、マルチラベルと合いません。
B：マルチラベル自体は合っていますが、ここでは「weight decay を意図どおりに効かせたい（混同を避けたい）」という条件があり、AdamWがより適切です。
D：softmaxはマルチラベルと合わず、MSEも分類では基本選びません。

■ まとめ

マルチラベル：sigmoid＋（logits版）BCE
weight decay を明確に効かせたい Adam 系：AdamW を選ぶのが定番です。
さらに深掘りしたい場合は、SGD・Adam・AdamWの更新式を見比べると整理しやすいです（AdamWはweight decayを分離しています）。

試験コアだけ読むルート

直前復習なら、ここだけで要点がつながります。

決定境界
単層は超平面で分けます。$w$が向き、$b$が位置です。
活性化関数
非線形を入れる部品です。シグモイドは確率出力向き、隠れ層はReLU系が多いです（飽和しにくいです）。
交差エントロピー
logは自信満々の外しを強く罰し、修正信号が強くなります。
逆伝播
計算グラフで「受け取った勾配 × 局所微分」を連鎖律で流します。
最適化
SGD基準で、モーメンタム（方向の平滑化）、Adam（平滑化＋スケール調整）、AdamW（weight decay分離）を押さえます。
実務の一般原理
確率を先に作ってからlogを取るより、logitsからlog-sum-exp系で安定に損失を計算します。

G検定×実務の最短ブリッジ

G検定の勉強が実務につながりやすくなるように、ニューラルネットを題材にします。
用語や部品を暗記するのではなく、どこで何がどのように使われているかを理解できることを目的にします。
そのために、試験で頻出の概念（決定境界・活性化・交差エントロピー・逆伝播・最適化）を、実務の定石（logits前提の損失、数値安定化、AdamW、不均衡対応）へ自然につなげます。

注意

本記事の数式モデルとPythonコードは補足扱いです。読み飛ばしても内容が分かるように書きます。
G検定では数式計算はほぼ問われないため、特徴と概念の整理を中心にします。

用語整理（logitsとlogitの混同防止）

本記事でいう logits は「（sigmoid/softmax で）確率に変換する前のスコア」を指します。
統計でいうlog-oddsのlogit（$ \log(\displaystyle \frac{p}{1-p}) $）とは混同しない前提で扱います。

（最終線形層の出力）logits → （確率への変換）sigmoid/softmax → 確率

ただし多クラス分類では、学習時にモデル側で softmax を明示せず、損失関数（交差エントロピー）が logits から内部で $\log\mathrm{softmax}$ を計算して安定に損失を求める実装が一般的です。
この場合、モデルの出力層は恒等（= logits をそのまま出す）になり、softmax は「損失関数の中で使われる」状態になります。

出力層×損失の対応表

試験でも実務でも混乱しやすいので、最初に固定します。

タスク	出力層が出すもの（推奨）	損失（フレームワーク非依存の言い方）	実務例（PyTorch）	試験の罠（ありがち）
二値分類（単ラベル）	スカラーlogits $z$	logitsから二値交差エントロピー（softplus/log-sum-exp系で安定化）	https://docs.pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html	sigmoidを前段に入れて二重にする / 確率BCEにlogitsを入れる
多クラス分類（単ラベル）	クラス別logits $z^{(k)}$	logitsから多クラス交差エントロピー（logsumexpやlog-softmaxで安定化）	https://docs.pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html	softmaxを前段に入れて二重にする
マルチラベル分類	ラベルごとlogits（独立）	各ラベル独立に二値交差エントロピー（logits版）	https://docs.pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html	相互排他なのにsigmoidを使う / 独立なのにsoftmaxを使う

判断基準（1行で固定）
ラベルが独立なら sigmoid + BCEWithLogits、相互排他（正解は必ず1つ）なら softmax + 交差エントロピーです。

予測したい確率の形（多クラス vs マルチラベル）

多クラス分類とマルチラベル分類の違いは「出力次元」ではなく、「正解の構造（確率の制約）」にある。どちらも出力層はベクトル状のlogitsを返すことが多いが、その後の解釈が違う。

多クラス分類（単ラベル）：1サンプルにつき正解クラスは必ず1つ（相互排他）
予測したいのは $p(y=k\mid x)$（$k=1,\dots,K$）のカテゴリ分布で、確率はクラス間で取り合いになり $\sum_{k=1}^K p(y=k\mid x)=1$ を満たす。
そのため logits から $\mathrm{softmax}$ で正規化し、交差エントロピーで学習するのが自然になる。
マルチラベル分類：1サンプルにつき正解ラベルは複数あり得る（0個もあり得る、非排他）
予測したいのは各ラベルごとの $p(y_i=1\mid x)$（$i=1,\dots,L$）で、確率に「合計1」の制約はない。
そのため各logitに $\sigma(\cdot)$（sigmoid）を適用し、各ラベル独立な二値交差エントロピー（BCE）で学習するのが自然になる。

実装上は、学習時に $\mathrm{softmax}$ や $\sigma$ をモデルに明示的に入れず、損失関数がlogitsから内部で安定に計算する（$\log\mathrm{softmax}$ や $\sigma$ 込み）ことが多い。この「置き場所」の違いが混乱の元になりやすい。

パーセプトロン→ロジスティック回帰→ニューラルネットワーク

横断理解を作るなら、この順番が分かりやすいです。

パーセプトロン
決定境界（超平面）で0/1を分ける発想です。ステップ関数は微分できないため、勾配ベース学習と相性が良くありません。
ロジスティック回帰
ステップ関数の代わりにシグモイドで0～1を出し、確率として扱えるようにします。交差エントロピーと組にすると学習の筋が通ります。
ニューラルネットワーク（多層化）
「線形→非線形」を積むことで表現力を上げます。誤差逆伝播が多層学習の現実解です。

この並びは、厳密な年代順として完全一致とまでは言い切れませんが、理屈として理解しやすく、試験と実務の両方に効く導線です。

決定境界

2次元入力 $x=(x_1, x_2)$ のとき、$w^\top x + b = 0$ は平面上の直線で、これが決定境界です。
$w$ は境界の向きを決め、$b$ は境界の位置をずらします。
単層（線形モデル）は、決定境界が直線（一般には超平面）になります。

活性化関数

活性化関数は非線形を入れる部品です。非線形がないと、層を重ねても線形のままで表現力が増えません。

シグモイド
出力が0～1になり確率として扱いやすいです。一方、飽和しやすく勾配が小さくなりやすいです。
ReLU系
隠れ層で実務の主流です。飽和しにくく学習が進みやすい傾向があります。

活性化関数の形（補足: グラフ）

以下は補足の可視化です。読み飛ばしてもOKです。

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

def relu(z):
    return np.maximum(0.0, z)

z = np.linspace(-6, 6, 2000)

plt.figure(figsize=(7, 4))
plt.plot(z, sigmoid(z), label="Sigmoid")
plt.plot(z, relu(z), label="ReLU")
plt.title("Activation functions")
plt.xlabel("z")
plt.ylabel("output")
plt.legend()
plt.tight_layout()
plt.show()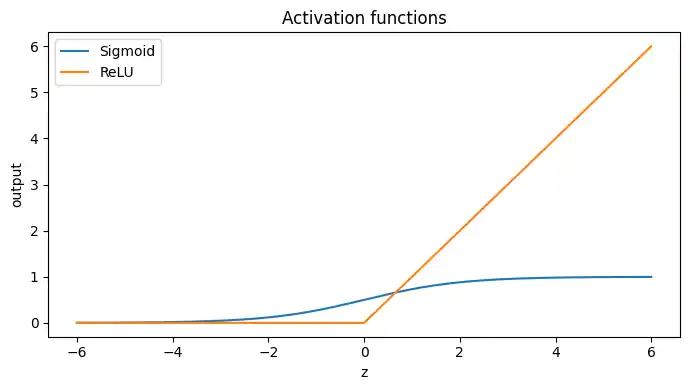

横軸zに対してシグモイドは0～1へ滑らかに変化し、ReLUは0より小さい範囲が0で0以上が直線的に増える様子を示す図 — シグモイドとReLUの形の比較（確率出力向きと隠れ層向きの直感）

交差エントロピーとlogの意味

交差エントロピーの直感は次の2つです。

logは「自信満々で外した予測」を強く罰します。
その結果、修正信号（勾配）が大きくなりやすく、学習が進みやすくなります。

G検定では数式を解かなくても、なぜlogが効くか、なぜ交差エントロピーが学習に向くかの説明ができると強いです。

同型で理解する数値安定化（BCEWithLogits と softmax交差エントロピー）

ここが「G検定×実務の最短ブリッジ」の中核です。二値と多クラスは別物に見えますが、安定化の発想は同型です。

フレームワーク非依存の言い換え
確率を作ってからlogを取るより、logitsからlog-sum-exp系で安定に交差エントロピーを計算します。

二値分類（BCEWithLogitsの形）

二値分類ではlogits $z$ から次の形に整理できます。
$L=\log(1+\exp(z)) – y z$

フレームワーク非依存の言い換え
sigmoidで確率を作らず、logitsからsoftplus（log-sum-exp）で二値交差エントロピーを安定に計算します。

実務例（PyTorch）
https://docs.pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html

多クラス分類（softmax交差エントロピーの形）

多クラスでは、真のクラスを $t$、各クラスのlogitを $z^{(k)}$ とすると次の形に整理できます。
$L=\log\left(\sum_k \exp(z^{(k)})\right) – z^{(t)}$

フレームワーク非依存の言い換え
softmaxを明示せず、logsumexp（log-softmax）で安定に交差エントロピーを計算します。

実務例（PyTorch）
https://docs.pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html

数値安定性の実害（expオーバーフロー→NaN）

softmaxを素直に計算すると、$\exp(\cdot)$ がオーバーフローしてinfが混ざり、inf/infでNaNが出ます。
logsumexp trickは「理論」ではなく「NaNを防ぐ安全装置」だと捉えると腹落ちが速いです。

以下は補足の可視化です。読み飛ばしてもOKです。

import numpy as np
import matplotlib.pyplot as plt

def softmax_naive(z):
    ez = np.exp(z)
    return ez / ez.sum()

def softmax_stable(z):
    z = z - np.max(z)
    ez = np.exp(z)
    return ez / ez.sum()

logits = np.array([1000.0, 999.0, 0.0])

naive = softmax_naive(logits)
stable = softmax_stable(logits)

text = (
    "logits = [1000, 999, 0]\n"
    f"np.exp(1000) = {np.exp(1000.0)}\n"
    f"naive softmax = {naive}\n"
    f"stable softmax = {stable}\n"
    "\n"
    "ポイント: expがinfになると、inf/infでNaNが出やすい"
)

print(text)

処理結果

logits = [1000, 999, 0]
np.exp(1000) = inf
naive softmax = [nan nan  0.]
stable softmax = [0.73105858 0.26894142 0.        ]

expのオーバーフローがNaNを生む例（logsumexp trickが必要になる実害）です。
logitsが大きいとexpがinfになり、素朴なsoftmaxがNaNを返す一方、安定版は有限の確率を返します。

試験の罠（現場事故にも直結）

softmax二重がけ

CrossEntropy系のlossは、内部でlog-softmax（logsumexpによる安定化）を取る前提で設計されていることが多いです。
softmax済みの確率を渡すと前提が崩れ、損失が不正確になります。
実務の裏取りとして、TensorFlowのAPIは「softmax済みを入れるな（不正確になる）」という趣旨の強い注意書きを置いています。
https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits

BCEの入力取り違え

確率を入力に取るBCEにlogitsを入れると前提が崩れます。
logitsを直接入れたいなら、logits前提のBCEWithLogits系を使います。
https://docs.pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html

マルチラベルの取り違え

ラベルが独立なら sigmoid + BCEWithLogits、相互排他なら softmax + 交差エントロピーです。
この判断基準だけを先に固定すると迷いが減ります。

逆伝播と計算グラフ

誤差逆伝播は、計算グラフ上で局所微分をつないでいく手続きです。
前向きで中間値を保存し、逆向きで「受け取った勾配 × 局所微分」を連鎖律で流します。
G検定では、連鎖律で掛け算がつながるため、深いネットで勾配が小さくなり得る（勾配消失）などの直感が問われやすいです。

不均衡データの実務チェックリスト（学習信号と運用判断を分ける）

不均衡データ（正例が希少）は頻出です。混ぜずに分けて整理します。

学習信号（モデルが学ぶ方向）

クラス重み
希少クラスの損失を重くして、学習で無視されにくくします。
リサンプリング
データ分布を調整して、学習が片寄りすぎるのを抑えます。

実務例（PyTorchのpos_weight）
https://docs.pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html

フレームワーク非依存の言い換え
希少クラスの誤りに強いペナルティを与え、学習で拾いやすくします。

運用判断（評価指標と閾値）

指標の選択
不均衡ではAccuracyが当てにならないことが多いです。目的に応じてPrecision/Recall、F1、PR AUCなどを使い分けます。
https://scikit-learn.org/stable/modules/model_evaluation.html
閾値調整
0.5固定が最適とは限りません。見逃しコストと誤検知コストに合わせて閾値を決めます。
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_recall_curve.html
確率を運用に使う場合
必要なら確率校正も検討します。
https://scikit-learn.org/stable/modules/calibration.html

最適化アルゴリズム（特徴で覚える）

G検定は更新式の暗記より、特徴が問われやすいです。SGDを基準に「何を足したか」で整理します。

SGD
勾配に学習率を掛けて引くだけです。
モーメンタム
方向に慣性（平滑化）を入れて振動を抑えます。
Adam
平滑化（1次）＋スケール調整（2次）で扱いやすい代表格です。
AdamW
weight decayを勾配に混ぜず、更新として分離する設計です。
https://arxiv.org/abs/1711.05101

最適化の挙動イメージ（補足: グラフ）

以下は補足の可視化です。読み飛ばしてもOKです。

import numpy as np
import matplotlib.pyplot as plt

a_coef, b_coef = 1.0, 24.0

def grad(theta):
    x, y = theta
    return np.array([a_coef * x, b_coef * y], dtype=np.float64)

def run_sgd(lr=0.08, steps=60, theta0=np.array([2.0, 2.0])):
    th = theta0.astype(np.float64).copy()
    path = [th.copy()]
    for _ in range(steps):
        th -= lr * grad(th)
        path.append(th.copy())
    return np.array(path)

def run_momentum(lr=0.08, beta=0.9, steps=60, theta0=np.array([2.0, 2.0])):
    th = theta0.astype(np.float64).copy()
    m = np.zeros_like(th)
    path = [th.copy()]
    for _ in range(steps):
        g = grad(th)
        m = beta * m + (1 - beta) * g
        th -= lr * m
        path.append(th.copy())
    return np.array(path)

def run_adam(lr=0.2, beta1=0.9, beta2=0.999, eps=1e-8, steps=60, theta0=np.array([2.0, 2.0])):
    th = theta0.astype(np.float64).copy()
    m = np.zeros_like(th)
    v = np.zeros_like(th)
    path = [th.copy()]
    for t in range(1, steps + 1):
        g = grad(th)
        m = beta1 * m + (1 - beta1) * g
        v = beta2 * v + (1 - beta2) * (g * g)
        mhat = m / (1 - beta1 ** t)
        vhat = v / (1 - beta2 ** t)
        th -= lr * mhat / (np.sqrt(vhat) + eps)
        path.append(th.copy())
    return np.array(path)

xs = np.linspace(-2.4, 2.4, 400)
ys = np.linspace(-2.4, 2.4, 400)
xx, yy = np.meshgrid(xs, ys)
zz = 0.5 * (a_coef * xx * xx + b_coef * yy * yy)

path_sgd = run_sgd()
path_mom = run_momentum()
path_adam = run_adam()

plt.figure(figsize=(6, 5))
plt.contour(xx, yy, zz, levels=30, alpha=0.7)
plt.plot(path_sgd[:, 0], path_sgd[:, 1], marker="o", markersize=2, label="SGD")
plt.plot(path_mom[:, 0], path_mom[:, 1], marker="o", markersize=2, label="Momentum")
plt.plot(path_adam[:, 0], path_adam[:, 1], marker="o", markersize=2, label="Adam")
plt.title("Optimizer trajectories on contours")
plt.xlim(xs.min(), xs.max())
plt.ylim(ys.min(), ys.max())
plt.gca().set_aspect("equal", adjustable="box")
plt.legend()
plt.tight_layout()
plt.show()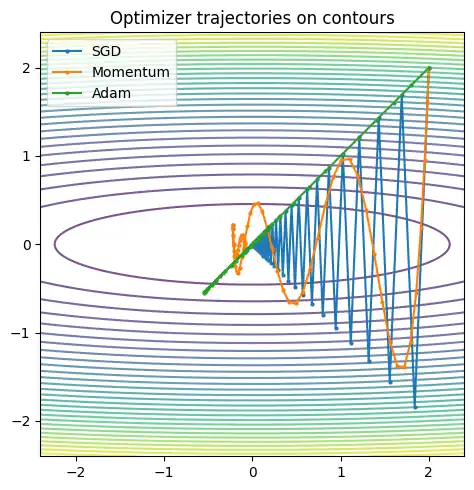

細長い谷の等高線上でSGD・モーメンタム・Adamの更新点が軌跡として描かれ、進み方の違いが分かる図 — 等高線上での更新軌跡（SGDのジグザグ、モーメンタムの平滑化、Adamのスケール調整の直感）

TensorFlow/Kerasでの同じ事故防止（フレームワーク横断の補強）

TensorFlowには「softmax済みを入れるな」に相当する強い注意書きがあるAPIがあります。
tf.nn.softmax_cross_entropy_with_logits は、内部でsoftmaxを行う前提なので、softmax出力を渡すと不正確になる趣旨の警告があります。
https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits

Keras側も from_logits の分岐で事故を避けられます。logitsを渡すなら from_logits=True、確率を渡すならFalseです。
https://www.tensorflow.org/api_docs/python/tf/keras/losses/CategoricalCrossentropy

FAQ

logitsとlogit（log-odds）は何が違いますか

本記事のlogitsは活性化（sigmoid/softmax）をかける前の未正規化スコアです。log-oddsを表すlogit（$\log(\displaystyle \frac{p}{1-p})$）とは混同しない前提で扱います。

softmax二重がけは何がまずいですか

loss内部でlog-softmax（logsumexpによる安定化）を取る前提が崩れます。その結果として勾配が痩せたり、学習が遅くなったりします。TensorFlowにも同趣旨の注意があり、softmax済みを渡すと不正確になる旨が書かれています。
https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits

CrossEntropyLossはsoftmax済みの確率を入れるものですか

違います。多くの実装は未正規化logitsを前提にしています。実務例（PyTorch）の公式ドキュメントも、その前提で説明されています。
https://docs.pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html

マルチラベルと多クラスはどう見分けますか

ラベルが独立ならマルチラベルなので sigmoid + BCEWithLogits です。相互排他（正解は必ず1つ）なら多クラスなので softmax + 交差エントロピーです。

AdamWのweight decayはL2正則化と同じですか

常に同じではありません。SGDでは近いものとして扱える場面が多いですが、Adam系では適応的スケーリングの影響でズレます。AdamWはweight decayを更新として分離し、このズレを避ける設計です。
https://arxiv.org/abs/1711.05101

参考文献

Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review. https://homepages.math.uic.edu/~lreyzin/papers/rosenblatt58.pdf
Rumelhart, D. E., Hinton, G. E., Williams, R. J. (1986). Learning representations by back-propagating errors. Nature. https://www.nature.com/articles/323533a0
Nair, V., Hinton, G. E. (2010). Rectified Linear Units Improve Restricted Boltzmann Machines. ICML. https://www.cs.toronto.edu/~hinton/absps/reluICML.pdf
Kingma, D. P., Ba, J. (2014). Adam: A Method for Stochastic Optimization. https://arxiv.org/abs/1412.6980
Loshchilov, I., Hutter, F. (2019). Decoupled Weight Decay Regularization. https://arxiv.org/abs/1711.05101
PyTorch Documentation: BCEWithLogitsLoss. https://docs.pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html
PyTorch Documentation: CrossEntropyLoss. https://docs.pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html
TensorFlow Documentation: tf.nn.softmax_cross_entropy_with_logits. https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits
TensorFlow Documentation: tf.keras.losses.CategoricalCrossentropy. https://www.tensorflow.org/api_docs/python/tf/keras/losses/CategoricalCrossentropy
scikit-learn Documentation: Model evaluation. https://scikit-learn.org/stable/modules/model_evaluation.html
scikit-learn Documentation: precision_recall_curve. https://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_recall_curve.html
scikit-learn Documentation: Probability calibration. https://scikit-learn.org/stable/modules/calibration.html
JDLA: 「G検定（ジェネラリスト検定）」シラバス改訂および公式テキスト第3版刊行のお知らせ（2024-05-14）. https://www.jdla.org/news/20240514001/
JDLA: シラバス（ダウンロードページ）. https://www.jdla.org/download-category/syllabus/

まとめ

G検定のニューラルネット頻出要点は、決定境界・活性化・交差エントロピー・逆伝播・最適化の1本線で整理できます。実務との最短ブリッジは「logitsからlog-sum-exp系で安定に損失を計算する」という一般原理で、二値（BCEWithLogits）も多クラス（softmax交差エントロピー）も同型です。さらに、出力層×損失の対応を固定し、softmax二重がけやBCEの入力取り違え、不均衡の評価設計を押さえると、試験でも現場でも迷いが減ります。

まとめのまとめ