はじめに
Python、ChainerによるLSTMにて日経平均株価の予測を試みる。
Chainerを使用しているのは、過去に実験的に作ったLSTMがChainerを使用しており、それを使いまわしているため。
ソースコードは最後の方に丸っと貼ってます。
LSTM以外にフーリエ変換、逆フーリエ変換を利用した分析/予測のシリーズもあり。(一応完結済み)
AI関連の記事はG検定のまとめ記事を中心にいろいろ記事を書いてるので興味ある方はこちらもどうぞ。
https://www.simulationroom999.com/blog/jdla-deep-learning-for-general-2020-1/
※ 文字数/画像数が多いためかページが重くなったので4ページに分割しました。
割とどうでもいいことなんだけど。
なんか株の銘柄が擬人化されてる。
株価の上がり下がりがそのまま感情表現になるとか。
さすが日本。気が狂ってる。(誉め言葉)

IRroid。すでにサービスは終了してるっぽい。
以降、真面目に行きます。
発端
うちの嫁に、
「株価予測するアプリ作れ」って脅された。
そもそも、それほど株取引の知識が無いのですけど。
とりあえず、それっぽいものを作るべくLSTMで実験した。
ちなみに嫁PCでも動作させる必要があったので、Pythonをexe化してPython環境構築しなくても動作させる必要があるのだが、それは別記事で記載してる。
結果
日足、週足レベルで見た場合に於いてはダメでした。
敗因は以下。
- 株価自体が何かルールを持っているわけではない。
- 外乱の塊をそのまま予測することは不可能。
- データ量が多ければ良いという感じでもない。
- 株価自体が基本的に緩やかな上昇をしているので、データ量を増やすと局所的な特徴が消え、緩やかな上昇という特徴だけが際立つ。
- 直近の予測が新型コロナの影響を受けすぎていて、なんか無理。
- 明らかな定性がある場合は、過去の定量など意味がない。
とは言っても月足レベルだと実はまぁまぁイケてることが分かって来て、地味においしく頂いております。
ソースコードは次ページ以降に置いてます。
用語
上で日足、週足、月足という言葉が出てきたので一応用語として貼っておきます。
単位期間を定め、単位期間中に初めに付いた値段を始値(はじめね)、最後に付いた値段を終値(おわりね)、最も高い値段を高値(たかね)、最も安い値段を安値(やすね)とし、この四種の値段(四本値=よんほんね)を「ローソク」と呼ばれる一本の棒状の図形に作図し、時系列に沿って並べて値段の変動をグラフとして表したものである。
Wikiepdiaより(https://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%BC%E3%82%BD%E3%82%AF%E8%B6%B3%E3%83%81%E3%83%A3%E3%83%BC%E3%83%88)
ローソクには、始値よりも終値が高い陽線(ようせん)と、始値よりも終値が安い陰線(いんせん)の2種類がある。
古くは陽線が赤、陰線が黒で書き表されていた事、値段が上ると明るい印象があり、下がると暗い印象がある事、相場の動きを陰陽道に絡めて考えた事などから陽線・陰線の名が付いている。
相場に関する印刷物が刊行されるようになった際、コストの高いカラー印刷を嫌って陽線を白抜きの四角形、陰線を黒く塗り潰した四角形で表示する様に変化し、現在の紙媒体では概ね白と黒で表示する。
始値と終値をローソク足の実体で、期間中の安値と高値はそこから伸びるヒゲで表現する。なお、4つの値のうち、2つ(ないしそれ以上)が同じ値になると、ヒゲや実体のない変則的なローソク足になる。
ローソク一つあたりの期間が一日の場合は日足(ひあし)、一週間の場合は週足(しゅうあし)、一月の場合は月足(つきあし)、一年の場合は年足(ねんあし)と呼ぶ。
予測結果
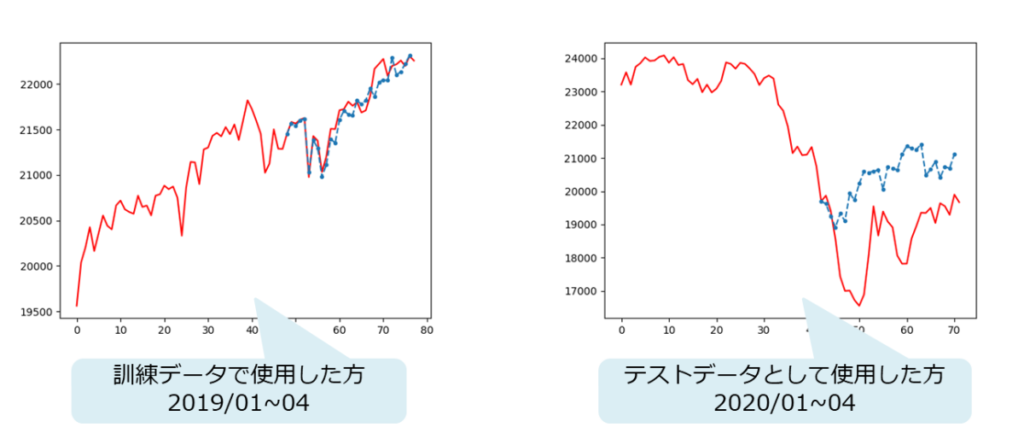
訓練データで使用した方はうまく予測している。
というか知っている波形なので予測と言ってよいのか・・・。
テストデータの方は全くだめ。
新型コロナの影響が大きすぎて、過去データが全く通用しない。
以下、技術的解説
分析手法
株価の分析手法は大きく2つに分かれる。
- ファンダメンタル分析
- テクニカル分析
今回実施する方式は後者に該当する。
ファンダメンタル分析
ファンダメンタル分析とは、財務諸表、健全性、経営、競争優位性、競合相手、市場などを分析することである。先物や為替に適用する場合は、経済、金利、製品、賃金、企業経営の全般的な状況に着目する。この用語は、他の種類の定量的な分析やテクニカル分析などの投資分析と区別するために使用されている。ファンダメンタル分析は過去と現在のデータを用いて行われるが、その目標は業績予想である 。個人投資家においては長期保有を前提に配当などの利回りを重視する立場をとる。大手機関投資家すなわち各銀行の含み益にも関係することから株価に全く無関心なことはないが、短期の上げ下げに一喜一憂しないアプローチ手法である。
Wikipediaより
最強のファンダメンタル株式投資法
外資系アナリストが本当に使っている ファンダメンタル分析の手法と実例
買い時・売り時がひと目でわかる 株価チャート大全
テクニカル分析
テクニカル分析(テクニカルぶんせき、英: technical analysis)とは、主に株式・商品取引・為替等の取引市場で、将来の取引価格の変化を過去に発生した価格や出来高等の取引実績の時系列パターンから予想・分析しようとする手法である。 将来の取引価格の予想を需給、収益性評価およびそれらの背景となる経済情勢分析に基づいて行う手法であるファンダメンタル分析と相対する概念である。判定ルールに多少なりともトレーダー自身の相場観や曖昧な視覚的判断を用いたものである場合、トレード手法としてはファンダメンタル分析と同じ裁量トレードに分類されるが、ルールを厳格化したりコンピュータ分析などを主体とするなどして、相場観や曖昧な視覚的判断を廃したルールを採用しているものについてはシステムトレードに分類される。またテクニカル分析とファンダメンタル分析以外にはアノマリーがある。
Wikipediaより
マーケットのテクニカル分析 ――トレード手法と売買指標の完全総合ガイド
株価チャートの教科書
テクニカル投資の基礎講座 ──チャートの読み方から仕掛け・手仕舞いまで
勝ち続ける投資家になるための 株価予測の技術[決定版]
Pythonで儲かるAIをつくる
アセットマネージャーのためのファイナンス機械学習
Pythonによるファイナンス 第2版 ―データ駆動型アプローチに向けて
内挿と外挿
学習と予測は、内挿と外挿の関係になる。
内挿の精度を上げると外挿がの精度が上がるかというとそうでもない。
今回の結果がまさにそれを語っている。
Excelで学ぶ時系列分析―理論と事例による予測―
LSTMとは
長・短期記憶(ちょう・たんききおく、英: Long short-term memory、略称: LSTM)は、深層学習(ディープラーニング)の分野において用いられる人工回帰型ニューラルネットワーク(RNN)アーキテクチャである。標準的な順伝播型ニューラルネットワーク(英語版)とは異なり、LSTMは自身を「汎用計算機」(すなわち、チューリングマシンが計算可能なことを何でも計算できる)にするフィードバック結合を有する。LSTMは(画像といった)単一のデータ点だけでなく、(音声あるいは動画といった)全データ配列を処理できる。例えば、LSTMは分割されていない、つながった手書き文字認識や音声認識といった課題に適用可能である。ブルームバーグ ビジネスウィーク誌は「これらの力がLSTMを、病気の予測から作曲まで全てに使われる、ほぼ間違いなく最も商業的なAIの成果としている」と書いた。
Wikipediaより
一言で言うと、
「系列データの予測が得意なRNNの拡張版で”勾配消失問題”、”将来に於いては関係があるデータの扱いの問題”の対策を入れたもの」
になる。
RNN、LSTMについては以下の記事でもう少し詳しく説明しているので、よろしければご参考に。
深層学習(ディープラーニング)とは
以下の記事を参照。
JDLA G検定の話も参考になるかも。
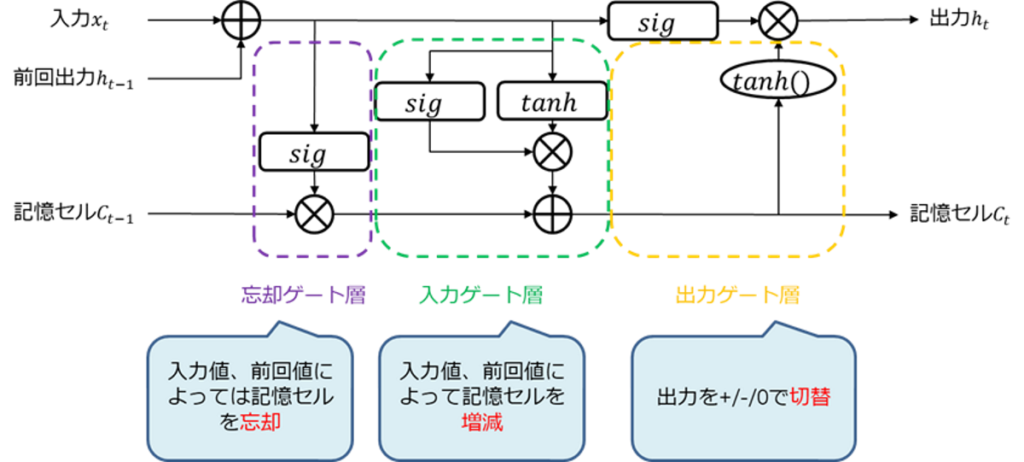
LSTMに学習させる際の注意点
LSTMは系列データの予測に強いと言っても、何でもOKというわけではない。
LSTMの構造上の都合で、以下の制約がある。
- ON/OFFスイッチ(シグモイド都合)
- プラス/マイナスの方向切替スイッチ(tanh都合)
よって、
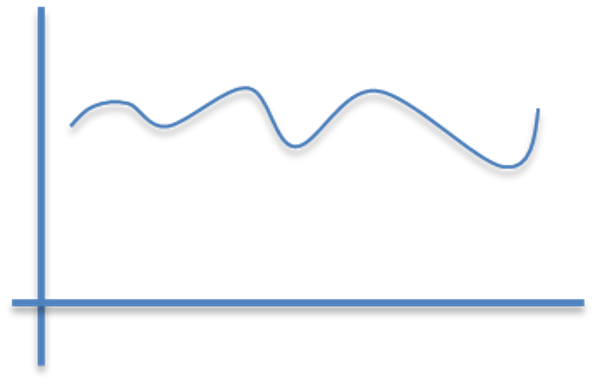
こういうのは常にプラス方向なので、LSTMの表現力が半減未満になる。
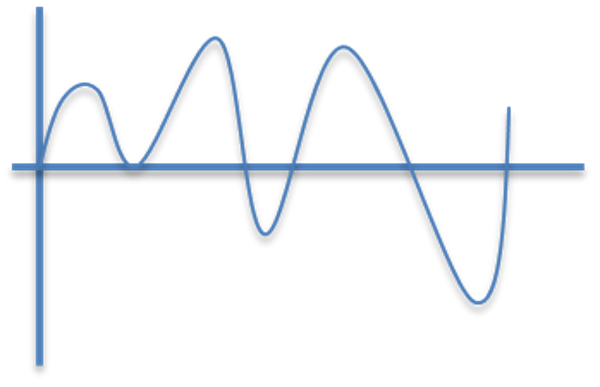
こういった感じの0を中心とした波形の方が得意。
さらに1.0未満だと尚良い。
データ加工方針
前項の理由により、そのまま株価を突っ込んでもLSTMの予測能力は期待できない。
よって、以下の方針でデータ加工する。
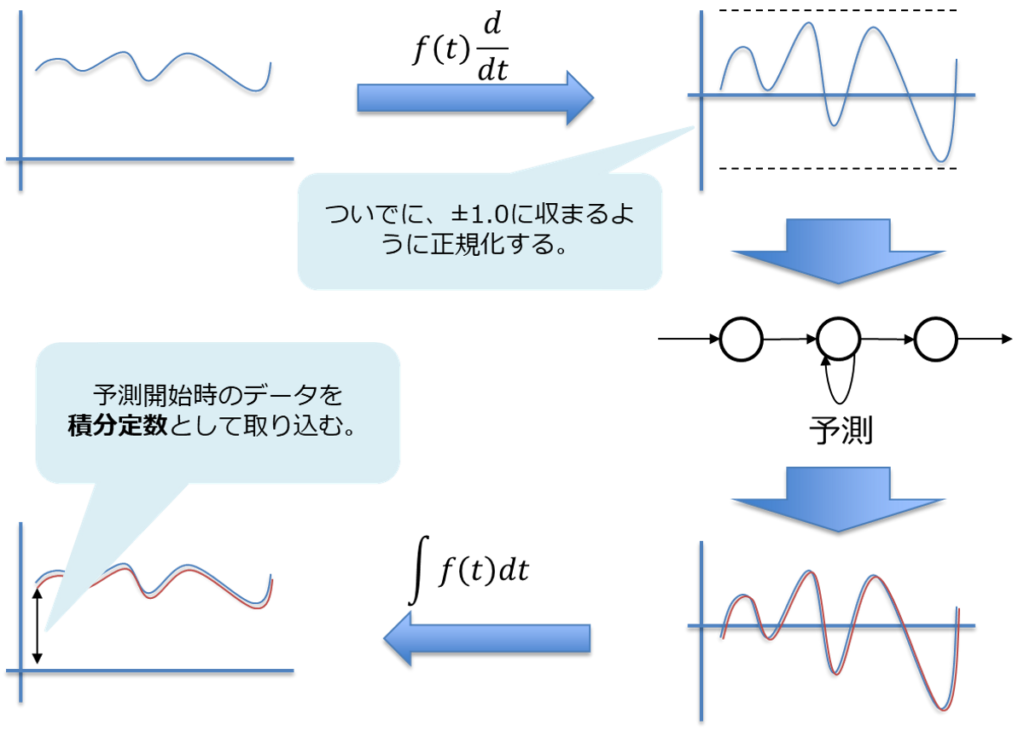
- 株価波形を微分する
- 微分した波形を±1.0に収まるように正規化する
- LSTMに学習&予測させる
- LSTMが予測した波形を不定積分する
- 不定積分した際に出てくる積分定数は予測直前のデータとする。
微分、積分について
積分、微分というキーワードを使ったが、やることは、引き算と足し算。
微分(差分法)
$$f(t)d/dt≒f(t)-f(t-1)≒f(t+1)-f(t)$$
積分(総和法)
\(C:\)積分定数
$$∫f(t)dt≒\displaystyle\sum_{i=1}^n f(t_i)+C$$
積分、微分の離散化の話は以下の記事を参照。
新 Excelコンピュータシミュレーション:数学モデルを作って楽しく学ぼう
Excelで操る! ここまでできる科学技術計算 第2版
工学のためのVBAプログラミング基礎
次のページへ
次は日経株価平均のデータ取得方法。












コメント