バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回、離散化の初歩として総和法、差分法を学び、原理としてテイラー展開を学んだ。
今回は離散化の基礎を押さえに行く。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
総和法の証明

では、
総和法をテイラー展開で証明してみよう。

うん。

テイラー展開の先頭から2項のみを使用する。
残りは切り捨て誤差扱いとする。
$$f(t)=f(t_0+Δt)≒f(t_0)+f(t_0)\frac{d}{dt}Δt$$

2項だけで良いの?

まぁ総和法の精度がこの程度なんだよ。
逆に言うと、第3項以降が総和法に於いての誤差ってことになる。

なるほど。

全体を積分する。
$$\int f(t) dt = \int f(t_0+Δt)dt = \int f(t_0)+f(t_0)Δt$$
\(f(t_0)Δt\)として解く。
$$f(t_0)Δt=\int f(t_0+Δt)dt – \int f(t_0)$$

この式を絵で描くとこんな感じ
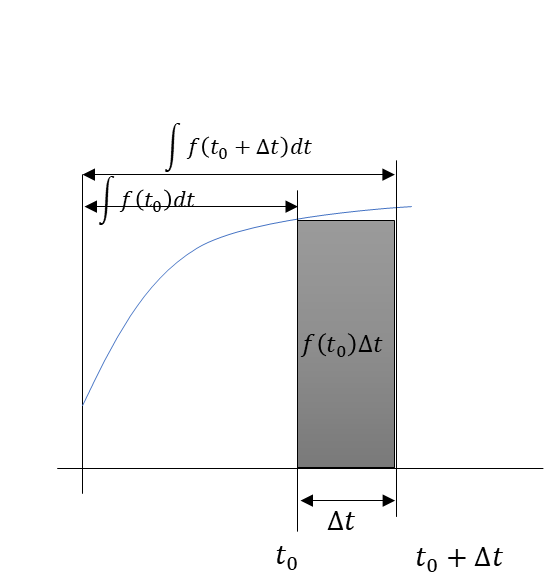

そして、解いた式の
$$\int f(t_0+Δt)dt – \int f(t_0)$$
って、定積分の公式そのものだったりする。

なるほど。
\(f(t_0)Δt\)は\(Δt\)の区間の定積分と近似ってことになるのか。

次は差分法かな。
差分法の証明

こちらもテイラー展開の先頭から2項のみを使用する。
残りは切り捨て誤差扱いとする。
$$f(t)=f(t_0+Δt)≒f(t_0)+f(t_0)\frac{d}{dt}Δt$$

総和法と同じく、第3項以降が差分法に於いての誤差だね。

\(f(t_0)\displaystyle \frac{d}{dt}\)に対して解く。
$$f(t_0+Δt)=f(t_0)+f(t_0)\frac{d}{dt}Δt$$
$$f(t_0)\frac{d}{dt}Δt=f(t_0+Δt)-f(t_0)$$
$$f(t_0)\frac{d}{dt}=\frac{f(t_0+Δt)-f(t_0)}{Δt}$$
絵に描くとこんな感じ。
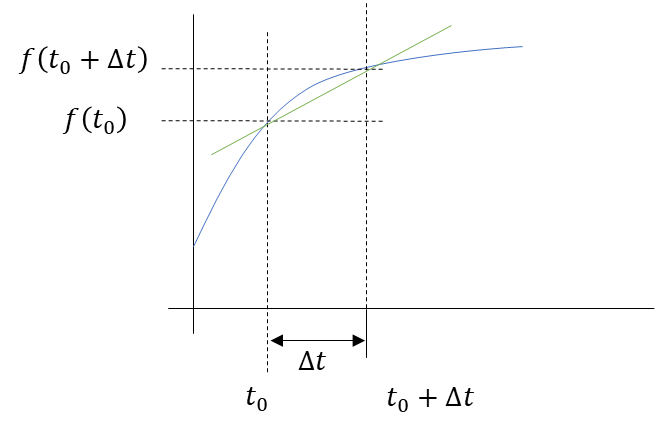

あれ?
これって微分を習ったときに見たような?

うん。差分方程式だね。
\(Δt→0\)にすると導関数となって、微分の定義になる。

おー!
なんか、頭の中で個別に有ったものが繋がったような感覚を覚えたよ!

と言う感じで、
それほど難しくはなかったでしょ?

うん。
モデル精度を上げるには?

総和法、差分法がテイラー展開の2項までしか使ってなかったわけだけど、
3項まで使うと精度が上がるってイメージ?

その認識で合ってるよ。
仕様でも、3項相当の式で誤差を小さくする仕様にしておいて、
実際は係数を0にすることで2項までしか使っていないってことも多い。

確かに見たことあるかも。
0掛けてるから、この項って要らないんじゃん?
って思ってたけど、
精度を引き上げる可能性を考えて入れていたってことだね。

たぶん。
まぁ、そうそうそこまでの精度は求められないから、
使われないことは多いけど。

ここまで来ると、3項のパターンも見たいなぁ(チラ)

じゃー次回ね。
(最初のころはあんなに食わず嫌いだったのに。。。)
まとめ

まとめだよ。
- 総和法、差分法はテイラー展開の第2項までを使用した式がベースになっている。
- よって、第3項以降が誤差となる
- 使用する項数を増やせば制度は上がる方向になる。
- 仕様上は3項までを想定、運用では2項までということが良くある。
バックナンバーはこちら




コメント