バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回、位置型PID制御とその欠点、そして速度型PID制御にすることでそれらが解消されることを説明。
次にソフトウェアに適用することになるが、それには離散化が必要。
今回は離散化について説明する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
どうやって離散化するのか?

んで、
前回のPID制御を離散化するんだっけ?

うーん、
今回はPID制御というよりも、
PID制御のように積分や微分を持った式を、
どのように離散的な近似関数にできるか、
という話の予定。

えー、
あんまり難しい話はやめてよー。

大丈夫。
一言で終わる。

ほんと?!何?

積分や微分の連続系から離散系に変換するのは・・・。

うんうん。

テイラー展開を応用している!

(あかん。さっぱりわからん。)
テイラー展開の前に初歩的な話

まぁ、
本当に一言で終わるとは思ってないよ。

んで、
そもそもテイラー展開って何?

テイラー展開の前に初歩的な話をしようか。

(こいつの初歩は本当に初歩な保証がないんだよなぁ)

離散化の初歩として以下がある。
- 積分は総和法で近似
- \(\displaystyle \int f(t)dt → \displaystyle \sum f(t-1)Δt+f(t)Δt \)
- 微分は差分法で近似
- \(f(t)\displaystyle \frac{d}{dt} → \displaystyle \frac{Δf(t)}{Δt}\)

・・・。

式で書くと良く分からないと思うけど、
絵で描いてみるとどうだい?
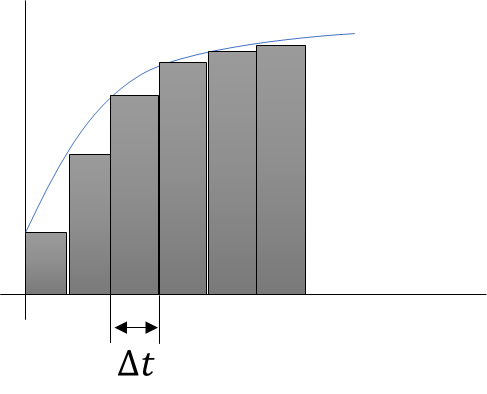
総和法
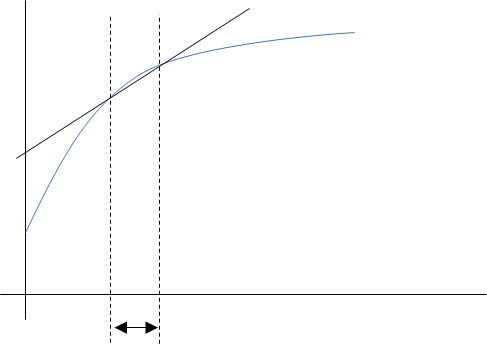
差分法

なるほど!
誤差は出ると言えば出るけど、
それなりに近似にする時のやり方だ!
これを先に出してもらわないと!

この話はおおよそ数値積分とか数値微分という「手法」の話で終わることが多い。
図示できるし、感覚とも一致するので受け入れやすいし納得し易いというのが最大の理由。
これを感覚で終わらせずにちゃんと原理としてテイラー展開で証明してみる。

(いや、もう総和法と差分法ってので良いんだけど。)
原理の話(テイラー展開)

んで、テイラー展開とは、
とある関数\(f(x)\)をとある点\(f(x_0)\)を用いて表現すると以下が成立するよって定理。
$$f(x)=f(x_0)+f(x_0)\frac{d}{dt}(x-x_0)+\frac{1}{2!}f(x_0)\frac{d^2}{dt^2}(x-x_0)^2+\frac{1}{3!}f(x_0)\frac{d^3}{dt^3}(x-x_0)^3 …$$

この”!”はなに?

階乗だね。
$$2!=1×2=2$$
$$3!=1×2×3=6$$
$$4!=1×2×3×4=24$$
という感じになる。

最後”…”があるってことは、これが無限に続くって感じ?

そうそう。
まぁ本当に無限に計算はしないから、
心配しなくても良いよ。

(こいつの「心配しなくて良い」は信用できん。)
テイラー展開の表現変更

とはいえ、
このままだとちょっと使い勝手が悪いので
式を若干変形する。

(もう何が使い勝手悪いのかすらわからん)

入力を変数\(x\)から時間\(t\)に置き換え、さらに\(t\)の定義を以下とする。
$$t=t_0+Δt$$

そして、
これをテイラーの定理式に入れ込む
$$f(t)=f(t_0+Δt)$$
$$=f(t_0)+f(t_0)\frac{d}{dt}Δt+\frac{1}{2!}f(t_0)\frac{d^2}{dt^2}Δt^2+\frac{1}{3!}f(t_0)\frac{d^3}{dt^3}Δt^3$$

あれ?
ちょっとシンプルになった?

うん。
\(f(t)=f(t_0+Δt)\)がかなり強い制約になるんで、
シンプルになるんだ。

んー。
すべてを理解したわけじゃないが、
何となく方向性が分かってきた気がする!

テイラー展開自体は、
何にでも対応できる式なんだけど、
今回の自分たちが使う範囲がそこそこ決まっているので、
前提条件を付加することで式がシンプル化して使いやすくしたって感じだね?

そうそう。
そのイメージ。
数式は単なるツールなんで、
それを自分の置かれた環境に合わせて前提条件を置いて単純化する。
というのが基本的なアプローチにある。

ちょっと食わず嫌いしてた感はあるなー。
といっても、
理解できたわけじゃないんだけど。

理解は追々でいいと思うよ。
実際、原理の話は「こういうのもあるんだ」程度で良くて、
最終的には総和法、差分法しか使わないってパターンが多いし。

あ、それそれ!
総和法、差分法だけじゃだめなの?

まぁ、
現実的には問題にはならないとは思うけど、
精度を引き上げたいとかの別の課題が出てくると詰むかな。

それでも、
まずは総和法、差分法だけでいいと思うんだけどなぁ。

「まずは」総和法、差分法で良いだろう。
この次はどうする?
そして最終的にはどうなってると良いと思う?

えー、いや、「まずは」なんでー。

何事も「まずは」で止まってはしまうことは問題ありかな。
「次は」「最終的には」も語れて、初めて「まずは」って話ができるんだ。
そうじゃないと、「まずは」が正しい方に向かってるかが分からなくなってしまう。

うーん、
言いたいことは分かるよ。
目的がハッキリしない行動は評価できないもんね。
「まずは総和法、差分法」「次にテイラー展開」「最終的には離散化の習得」というイメージが大切ってことだよね。

「まずは初歩」
「次に原理」
「最終的に基礎」
と言い換えても良いね。

なるほど。
それで最初に「初歩的な話」って言い方をしていたんだね?
確かに「初歩」と「基礎」は別物だなぁ。

そういうこと。

ちょっと、
一旦自分で今回の話を整理したいんで続き次回で良いかな?

うん。
私もそのつもりでいた。

じゃー次回ー。
まとめ

まとめだよ。
- 離散化はテイラー展開を応用して実現している。
- テイラー展開に\(f(t)=f(t_0+Δt)\)の制約を掛けると式が単純化される。
- 総和法、差分法は初歩、テイラー展開は原理、そのあとに離散化の基礎。
- 初歩の後に原理、原理の後に基礎を押さえておくと良い。
バックナンバーはこちら




コメント