バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、離散フーリエ変換、逆離散フーリエ変換のバリエーションについて説明。
1/Nに伴う数式対称性によるバリエーションがある点に注意が必要。
そして今回からが本命のFFT、IFFTへ。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
FFT、IFFTのバリエーション

まず最初に言っておくと、FFT、IFFTのバリエーションは
離散フーリエ変換(DFT)、逆離散フーリエ変換(IDFT)と同一だ。
よってバリエーションの話は終了。

まさかの一言で終了?!

ん?
ってことはDFTとFFTは同一のもの?
あれ?そうだっけ?

FFT、IFFTはDFT、IDFTを
とあるアルゴリズムを元に高速化したものだ。
よって、ベースとなる数式は同一なんだよね。

なるほど。
数式は同一なんだけど、演算方法が違うってだけなのか。

まぁその演算方法の都合、入力する時間領域の「サンプリングデータは2のべき乗」じゃないと使えないんだけどね。

そういえばそういう話は良く聞くなぁ?
なんで2のべき乗じゃないとダメなんだ?

バタフライ演算ってのをやってるから。

そのバタフライ演算ってのは・・・?
回転因子

バタフライ演算の前に回転因子について説明しよう。

回転因子?

オイラーの公式を覚えてる?

たしかこんなのだったよね?
\(e^{i\theta}=cos(\theta)+i sin(\theta)\)

そうそう。
そして、離散フーリエ変換、逆離散フーリエ変換で使用される指数関数はこんな感じだ。
\(\displaystyle e^{-i\frac{2\pi tx}{N}}\)
\(\displaystyle e^{i\frac{2\pi tx}{N}}\)

ポイント\(2\pi\)が入っている点で、
ここだけに着目すると、cos、sinの三角関数は必ず1周以上する。

うん。
単位がラジアンで考えると\(2\pi[rad]\)は\(360^{\circ}\)だもんね。

そして、サンプリング数、周波数数を決定する\(N\)で割ってる。

ということは、1周がN分割されてる????

この性質を利用したものが回転因子だ。
表現方法は以下になる。
\(W_N^n=\displaystyle e^{-i\frac{2\pi n}{N}}\)

イメージし易いよう\(N=8\)の場合の複素平面上の配置も出しておこう。
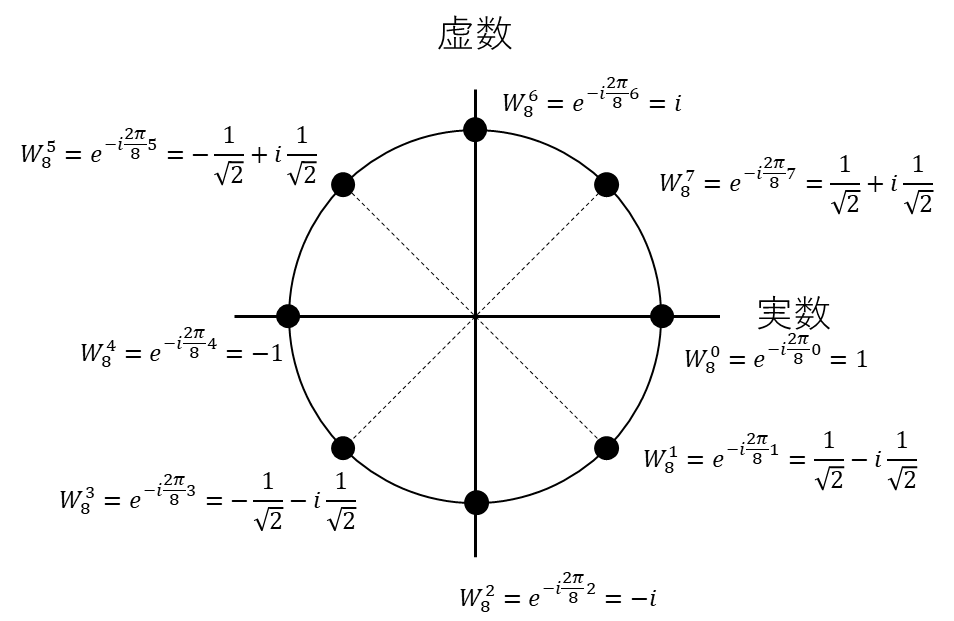

おー!
そうか、三角関数で表現し直せるから、こういう位置関係になるのか!

これはオイラーの公式様様って感じだね。

この回転因子のイメージがあるとこの先の説明が分かりやすくなると思うよ。
まとめ

まとめだよ。
- FFT、IFFTの数式上のバリエーションはDFT、IDFTと一緒。
- 元にしている数式自体は同一。
- FFT、IFFTはバタフライ変換による高速化を行ってる点で異なるのみ。
- バタフライ変換を理解するためには回転因子のイメージが重要。
- オイラーの公式のおかげで複素指数関数と三角関数が紐づく。
バックナンバーはこちら。




コメント