バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回はバタフライ演算向けての回転因子の最適化を実施。
複数段の行列が定義でき、中間変数を挟むことで演算を単純化できそうなのはわかってきた。
今回はここからバタフライ演算へ繋げる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
中間変数を置いた行列演算再掲

まずは前回の行列演算を再掲しておく。
\(
\begin{bmatrix}
G_0 \\
G_1 \\
\end{bmatrix}
=
\begin{bmatrix}
W_2^0 & W_2^0 \\
W_2^0 & W_2^1 \\
\end{bmatrix}
\begin{bmatrix}
f_0 \\
f_2 \\
\end{bmatrix}
\)
\(
\begin{bmatrix}
G_2 \\
G_3 \\
\end{bmatrix}
=
\begin{bmatrix}
W_2^0 & W_2^0 \\
W_2^0 & W_2^1 \\
\end{bmatrix}
\begin{bmatrix}
f_1 \\
f_3 \\
\end{bmatrix}
\)
\(
\begin{bmatrix}
F_0 \\
F_1 \\
F_2 \\
F_3 \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & W_4^0 & 0 \\
0 & 1 & 0 & W_4^1 \\
1 & 0 & -W_4^0 & 0 \\
0 & 1 & 0 & -W_4^1 \\
\end{bmatrix}
\begin{bmatrix}
G_0 \\
G_1 \\
G_2 \\
G_3 \\
\end{bmatrix}
\)
バタフライ演算

じゃ、前回の行列演算を図示してみたのが以下になる。
青のラインが単純加算で、オレンジのラインは何かしらの係数を掛けた上での加算を示している。
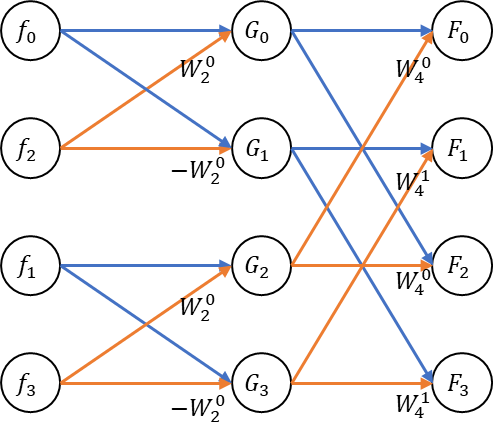

なんか交差してる感じが蝶々みたいな感じだねー。

ん?蝶々?

もしかして、これがバタフライ演算の名前の由来とか?!

正解。
ビットリバース

バタフライ演算が何者かはわかったけど、
入力の\(f_0\)~\(f_3\)って順番がいれかわってるじゃん?
この入れ替えがあるとアルゴリズムとしての実装は難しいんじゃないかなー。

ここはビットリバースのルールに準じてるな。

よくわからんけど、なんか簡単に出来るルールがあるんだ。

今回のN=4の場合だと以下になる。
| 元の行 | 2進数 | 2進数逆転 | 入れ替え先行 |
|---|---|---|---|
| 0 | 00 | 00 | 0 |
| 1 | 01 | 10 | 2 |
| 2 | 10 | 01 | 1 |
| 3 | 11 | 11 | 3 |

あ、今回の入れ替え順番になったね。
CooleyTukey型FFTアルゴリズム

というわけで、これら一連の流れをアルゴリズムとしたものを
「CooleyTukey型FFTアルゴリズム」って呼ばれてる。

ということは他にもあるってこと?

あるらしいけど、CooleyTukey型が一番有名で、他のアルゴリズムはあんまり知らないんだよね。

でも、なんか高速化できそうってのはわかってきたぞ。

ちなみに、このバタフライ演算を行う構成の都合上、入力サンプリングは2のべき乗になる。

「入力サンプリングは2のべき乗」ってのは以前言ってたね。
たしかに、高速化しようと思うとバタフライ演算が必要。
バタフライ演算は入力サンプリングが2のべき乗。
ってのは納得だ。

と言う感じでかなり端折っている部分は有れど、フーリエ変換からFFTまでの概要は終了だ。

あれ?
IFFTの方はどうなるの?

IFFTの方は回転因子の配置方向が逆になるだけで、考え方は全く一緒だ。

あ、そっか。指数関数の指数部の符号が逆になってるだけだもんね。

そうそう。
まとめ

まとめだよ。
- バタフライ演算を図示した。
- 演算が交差している様が蝶々のようなのでバタフライ演算と呼ばれている。
- 入力サンプリングの入れ替えルールはビットリバースに準じている。
- これら一連の流れを「CooleyTukey型FFTアルゴリズム」と呼ぶ。
- このアルゴリズムは入力サンプリングが2のべき乗であることが前提。
バックナンバーはこちら。




コメント