https://www.simulationroom999.com/blog/derivation-of-motor-transfer-function/
フレミングの左手の法則より、磁界の中を長さ\(l\)の導体に電流\(I_m\)を流すとローレンツ力\(F\)が発生する。
\(B\):磁界密度
\(l\):磁界の中の導体\([m]\)
\(F\):ローレンツ力\([N]\)
\(T_r\):ロータートルク\([N・m]\)
\(r\):回転軸から導体までの長さ\([m]\)
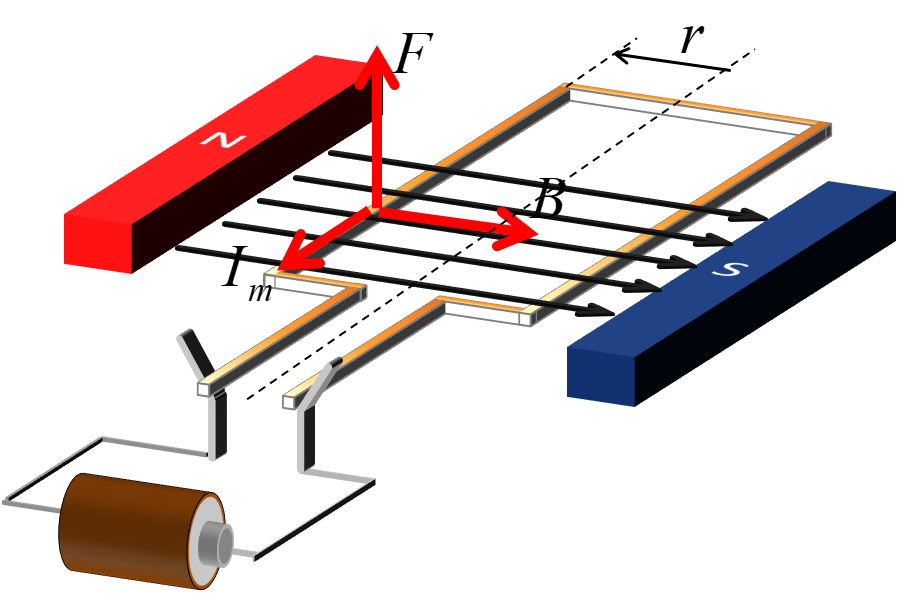
以下の式であらわされる。
$$F=BlI_m$$
トルクは力\([N]\)とそこからの距離\([m]\)のクロス積(外積)。
力学では、トルク\(T\)は次のように定義される。
トルクの定義
$$T=F×r$$
\(F\) は物体に加わる力、\(r\) は回転の軸からみた力の加わる点までの距離。
よって、回転半径\(r\)とローレンツ力\(F\)から以下の式になる。
$$T_r=F×r=BlI_m×r=BlI_mrsin(θ)$$
ローターを完全剛体とすると回転半径\(r\)とローレンツ力\(F\)は常に直交していると言える。
よって、計算としては以下と解釈して良い。
\begin{align}
θ&=90°\\\\
sin(θ)&=1\\\\
BlI_mrsin(θ)&=BlrI_m\\\\
\end{align}
\(Blr\)は定数であるため、\(K_t\)としてまとめる。
\begin{align}
K_t&=Blr\\\\
T_r&=K_tI_m\\\\
\end{align}
ここで出てくる\(K_t\)はトルク定数と呼ばれるものである。
モーターの発電原理で出てきた逆起電力定数\(K_e\)も\(Blr\)をまとめたものである。
よって、トルク定数\(K_t\)と逆起電力定数\(K_e\)は同じ値になる。
$$K_t=K_e$$
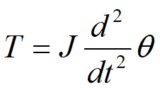
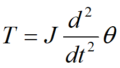

コメント