はじめに
- モーターの伝達関数そのものはググればそれなりに出てくる。
- しかし、どのように導出したかわからなければその後の調整、応用ができなくなる。
- よって、導出過程を見た上で応用を考える。
本記事を元に作ったモデルは以下の記事で説明している。
合わせて参照してもらえると良いと思う。
Scilab版
MATLAB/Simulink版
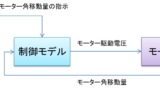
全体の流れ
凡その以下の流れの話となる。
- モーターの等価回路から、電圧から電流の伝達式を導出
- モーターの発電原理から角速度から逆起電力の伝達式を導出
- モーターのトルク原理から、電流からトルク、角加速度の伝達式を導出
伝達関数
モーターMILSで使用した伝達関数は以下となる。
\(I_m\) : モーター電流\([A]\)
\(E_m\) : モーター電圧\([V]\)
\(E_{ke}\) : 逆起電圧\([V]\)
\(L_m\) : モーターインダクタンス \([H]\)
\(R_m\) : モーター抵抗\([Ω]\)
$$\frac{I_m}{E_m-E_{ke}}=\frac{1}{L_m s+R_m}$$
意味としては\(E_m-E_{ke}\)から\(I_m\)への伝達は\(\frac{1}{L_ms+R_m}\)になる。
分子が入力、分母が出力とした伝達関係を表す。
Scilab/xcosやMatlab/Simulinkには伝達関数ブロックがあるので、この式を導出するのがプラント作成のキモとなる。
モーターの構造
餅は餅屋、モーターはモーター屋ってことでマブチモーターのwebサイトでモーター構造の確認。
あとは書籍からとか。
入門 モータ制御:実務に役立つ制御の考え方

史上最強カラー図解 最新版 モータ技術のすべてがわかる本
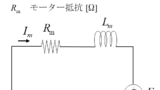
電気的には巻線(コイルと抵抗)と巻線が回転時に発生させる逆起電圧にて構成される。
モーター等価回路編
電気的特性からでは逆起電圧\(E_{ke}\)の算出はできない。
よって、モーターの発電原理を元に逆起電圧\(E_{ke}\)を求める必要がある。
発電原理/逆起電力編
逆起電圧を求めるには角速度ωを求める必要がある。
そして、運動方程式から角速度ωの伝達関数を求める必要がある。
運動方程式編
あとはロータートルク\(T_r\)を算出すれば、モーターとしての伝達関数は完成する。
トルク発生原理編
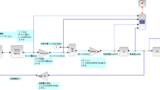
伝達関数編
伝達関数分解/再構築編
まとめ
- プラント設計においては伝達関数が命
- 極端な場合だと伝達関数一個でプラントが完成する。
- ただし、伝達関数ですべてを解決させようとすると、ちょい修正を行う場合、命取りにもなる。
- 伝達関数の分解ができれば、動作を変えずにパラメータの分解ができる。
- 基本的には負帰還が増えるような構成になる。
- ラプラス変換にアレルギーな人もいるかもしれないが、とりあえず微分⇒(s)、積分⇒(1/s)とだけ覚えておけばしばらくは安泰。
- あとは普通の代数方程式で解ける。
- 面倒臭い微分、積分をスルーできる便利なツールとでも思っておけば良い。
弱点克服 大学生の初等力学
電子回路入門講座
電気回路入門講座
文系でもわかる電気数学: “高校+αの知識”ですいすい読める
「Maxima」と「Scilab」で学ぶ古典制御: 「ラプラス変換」「伝達関数」から「フィ-ドバック制御」まで (I/O BOOKS)
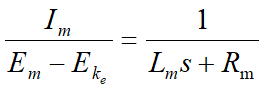


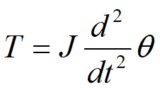




コメント