https://www.simulationroom999.com/blog/derivation-of-motor-transfer-function/
はじめに
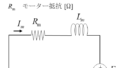
モーターの発電原理を元に逆起電力について説明が可能。
逆起電力定数
フレミングの右手の法則より、
磁界の中を長さ\(l\)の導体が速度\(v\)で移動すると起電圧\(e\)が発生する。
$$e=Blv$$
\(B\):磁束密度
\(l\):磁界の中の導体長\([m]\)
\(v\):導体の速度\([m/s]\)
\(e\):起電圧\([V]\)
\(r\):回転軸から導体までの長さ\([m]\)
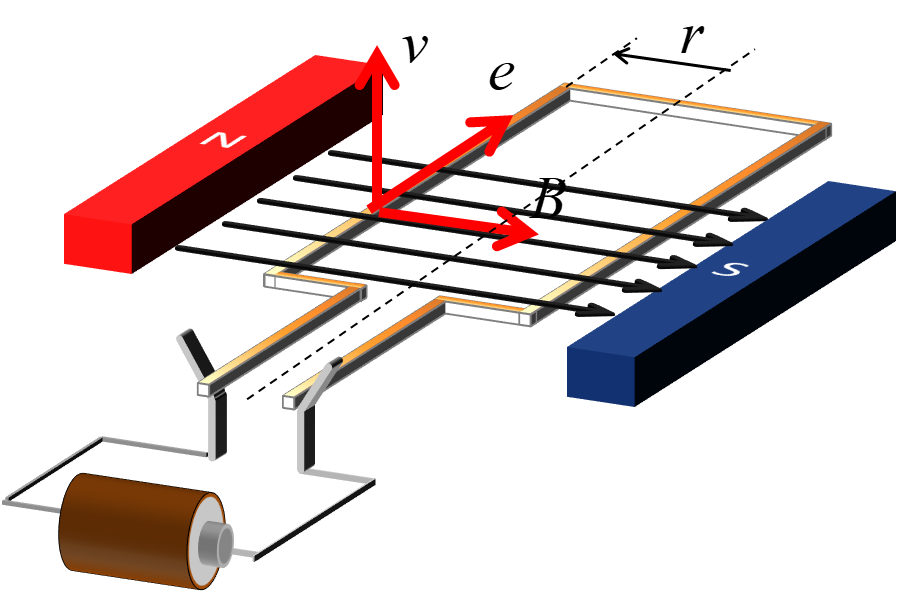
回転運動をしているため、速度\(v\)は回転半径\(r\)と角速度\(ω\)の乗算と等価となり、以下の式になる。
$$e=Bl(rw)$$
\(Blr\)は定数であるため、\(K_e\)としてまとめる。
$$K_e=Blr$$
$$e=K_eω$$
$$E_{ke}=K_eω$$
ここで出てくる\(K_e\)は逆起電力定数と呼ばれるものである。
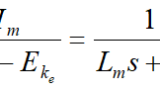
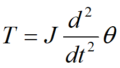
コメント