バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-motor-backnumber/
はじめに
モータの
電力=仕事率
動力=仕事率
であることから、
モータは「電気、力学の間のエネルギー保存の法則を最も簡単に実現してくれる装置」
であることを知った太郎くん。
今回は仕事率についてフクさんから説明を受ける。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
仕事率の話の前に?

仕事率の説明をするんだったかな。

うんうん。

仕事率の前に、
力学に於いての主要な物理量を一回整理しようか。

そうしてもらえると助かるよ。
高校、大学で聞いた気はするんだけど・・・
実は、
公式を丸暗記して乗り切ったから、
良く分かっていないんだよね。

まぁそういう人は多いだろう。
丸暗記というのも実は悪いアプローチではない。
ただし、
一緒に関係性も覚えておくと悩まなくて済んだかもね。

どういうこと?

今回、私も細かく説明する気はない。
主要な物理量とその関係性だけを知ってもらって、
モデルベース開発に対して、「どう利用できるか」程度に留めようと考えている。

そうだね。
僕も細かいこと言われても多分理解できないから、
「どう利用しているか」ってポイントに絞ってもらった方が
助かるよ。
主要な物理量について

まず力学には直線運動と回転運動がある。

うっすらと覚えてる。

別の言い方をすると、
直線運動=直交座標系
回転運動=極座標系
という感じになる。

ざ、座標・・・系?

今回は特に座標ことベクトル的な話はしないので、
言葉だけ覚えておけばいいよ。

それならOK!

そして、電気の方は電流、電圧、電力、電力量というのがある。

えーっと、
電流×電圧で電力だっけ?
あれ?
電力量ってなんだっけ?

それも後で説明するよ。

うん。期待してる。

直交座標系、極座標系、電気、
3つの領域の
主要な物理量を説明するよ。
直交座標系の主要な物理量

力、運動量、仕事、仕事率
というものがある。

お、おう。

基本的な物理量は力で単位は\([N]\)(ニュートン)になる。

アイザック・ニュートンが見つけて、
名前が単位になってるんだよね。
(僕が何か新しい物理量を見つけたら名前が単位になるのだろうか?
1太郎、2太郎・・・)

力、運動量について、
とりあえず計算する上で便利な概念とだけ思っておけば良い。

え?
それでいいの?
リンゴが重力でどうのって話はいらない?

今回に限っては不要。

よし!
じゃんじゃん行っちゃって!!

(とりあえず、可能な限り頭を使わせない方針は正しかったようだ。)

ざっと関係性だけ説明するよ。
- \(運動量=力×時間\)
- \(仕事=運動量×速度\)
- \(仕事率=仕事÷時間\)

なんか時間と速度で掛けたり割ったりなんだね。

そうそう。
さらに時間と速度を掛けると距離だよね?
あと、時間を掛けて後に時間で割ると時間というパラメータは無くなるよね?

うん。そうだね。

よって、
- \(仕事=力×時間×速度=力×距離\)
- \(仕事率=力×時間×速度÷時間=力×速度\)
となる。

おー!なんかシンプルだ!
そういえば、仕事は
「物体に一定の力を掛けつづけて一定距離移動したもの」
って習った気がする。
言葉じゃなくて、掛け算割り算で覚えれば良かったのか!

そういうこと。
そのまま次は極座標系に行くよ。

がってん!
極座標系の主要な物理量

基本的には直交座標系と考え方は一緒。
力がトルク、運動量が角運動量に変わる程度。

トルク、角運動量が何者かは全く分からないけど、
分からなくてもいいような説明を期待するよ!

(こいつは・・・)

こんな感じだよ。
- \(角運動量=トルク×時間\)
- \(仕事=角運動量×角速度\)
- \(仕事率=仕事×時間\)

さらに直交座標系と同じように、
- \(仕事=トルク×時間×角速度=トルク×角度\)
- \(仕事率=トルク×時間×角速度÷時間=トルク×角速度\)

よかった。予想通りで。

ところで、
仕事と仕事率は直交座標系と極座標系で同じものと考えて良いの?

厳密には異なる物だけど、
今回に限っては一緒と思って良いよ。

うん、思っとく。

次は電気かな。
電気の主要な物理量

さっき言ったように
- 電流
- 電圧
- 電力
- 電力量
がある。

うんうん。
これも関係性があるんだよね。

関係性はこんな感じだ。
- \(電圧=電流×抵抗\)
- \(電力=電流×電圧\)
- \(電力量=電力×時間\)

あれ?
直交座標系と極座標系の両方に出てきた仕事と仕事率は?
仕事と仕事率でうまく繋がると思ってたんだけど。

ほう。意外と考えていたんだな。

意外とは失礼な!

まぁまぁ。(完全に思考停止していると思ってた)

実は、電力量が仕事で、電力が仕事率と等しくなる。

ということは、
電圧と電流が分かれば、
仕事と仕事率が分かるってことか!

その通り。

モータに限らず、
仕事と仕事率で異なる物理領域を横断しているものは多い。
今回は説明しないけど、熱学も熱が仕事で熱流が仕事率になる。

へー。
仕事と仕事率で考えると結構楽になるんだね。
力学と電気の関係性

とりあえず、さっきまでの話を表と絵にまとめたよ。
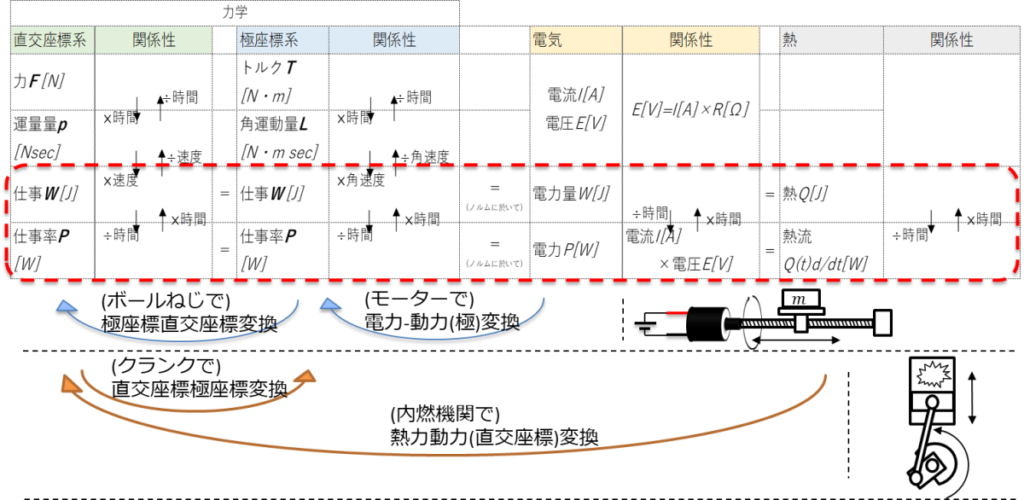

おー。
見事に仕事と仕事率が横断してるね。
モータだけでなく、
エンジン(内燃機関)も同じ発想で変換できるんだ!

そうそう。

よし!
これでモータはバッチリだ!
電流と電圧を掛ければ電力で、
これは仕事率だから極座標の仕事率と一緒になるもんね。

まぁ理想はそうなんだけどね・・・

え?
理想は・・・?
現実は違うの?

それは次回に説明しようかな。

(続くのか)
まとめ

まとめは以下な感じだよ。
- 力学(直交座標、極座標)、電気の主要の物理量は時間、速度との関係性で覚えると楽。
- 力学(直交座標、極座標)、電気で共通の物理量として仕事と仕事率がある。
- 熱学のような他の領域でも仕事と仕事率に相当するものがあるので、エネルギー変換を考える際はとても便利。
バックナンバーはこちら




コメント